基于定点迭代方法的自适应数字预失真器
吴长奇,张晓娟
(燕山大学信息科学与工程学院,河北秦皇岛 066004)
0 引言
高阶线性调制方式具有功率有效和频带有效的优点,但其包络起伏大,通过非线性的高功率放大器(high power amplifier,HPA)时会产生频谱扩展,造成邻信道干扰。预失真技术是克服放大器非线性的有效方法。数字基带预失真算法由于频带宽,稳健性好,且易于用DSP实现而应用广泛[1-2]。
基带预失真算法包括数据预失真和信号预失真两类。数据预失真[3-4]在发送滤波器前对信号的星座图进行预矫正,因此预失真效果受信号星座和发送滤波器记忆效应的影响。信号预失真[5-10]则在发送滤波器后对信号幅度进行矫正,克服了以上缺点。信号预失真中的复增益结构模型所用查找表(look-up table,LUT)尺寸最小、结构最简单而为本文采用。
目前的自适应预失真算法主要包括线性法、割线法和离散牛顿法,其中线性法收敛速度最慢,割线法和离散牛顿法收敛速度相当。本文提出一种定点迭代预失真器,即将预失真过程看作定点迭代问题,通过逐次逼近的方法获得查找表的最佳值,利用Steffensen加速方法后,预失真器至少具有平方敛速。
1 系统模型
高速卫星通信系统的等效基带模型如图1所示。调制器产生幅度-相位调制(amplitude phase shift keying,APSK)信号,脉冲成形滤波器和匹配滤波器具有奈奎斯特平方根升余弦特性。行波管放大器(travelling wave tube amplifier,TWTA)代表星上处理器,只考虑上行链路噪声。
1.1 TWTA模型
设TWTA的等效基带输入信号为

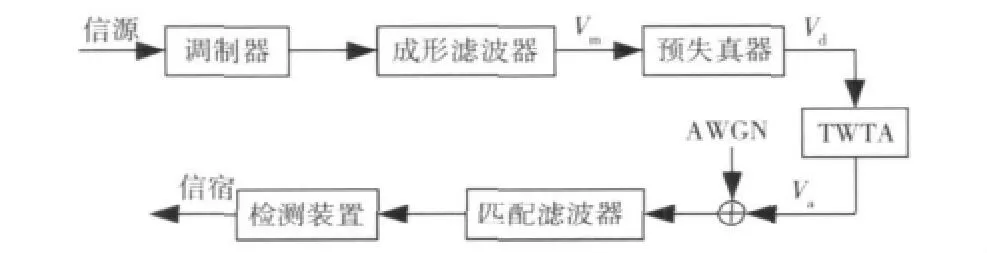
图1 卫星通信系统模型Fig.1 Satellite communication system model
(1)式中,r(t)和φ(t)分别表示调制包络和相位。
TWTA的输出记为
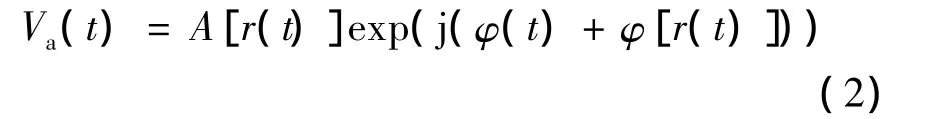
(2)式中,A[r(t)]和φ[r(t)]分别表示TWTA的幅度/幅度(AM/AM)转换特性和幅度/相位(AM/PM)转换特性。采用Saleh[11]提出的TWTA模型,有

(3)-(4)式中:r表示归一化输入幅度;TWTA的模型参数为αA=2,βA=1,αφ=π/3和βφ=1。Cavers[7]提出将高功率放大器的输入-输出关系视为复增益函数,即令

图2是TWTA的输入-输出曲线,纵坐标为输出电压对最大饱和输出的归一化。可以看出,放大器工作点越接近饱和区,非线性失真也越严重。采取功率回退的方法可以获得线性性能,但功率转换效率也会随之降低。
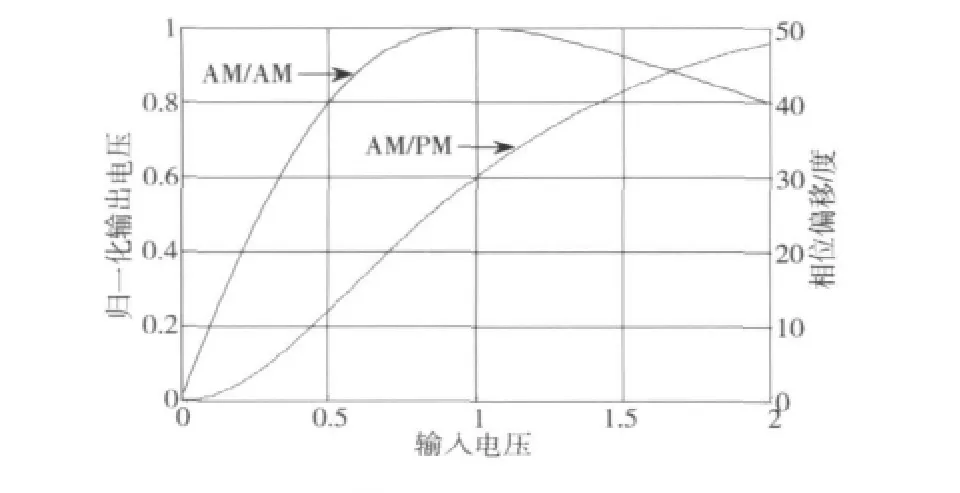
图2 TWTA的AM/AM和AM/PM曲线Fig.2 AM/AM and AM/PM characteristics of TWTA
1.2 预失真器结构
放大器性能会随着信道突变、温度漂移和供给电压的变化而变化,因此要求预失真器(predistorter,PD)能够跟踪放大器的性能变化,这就需要自适应预失真器,其结构如图3所示。矩形框内代表PD,Vm为PD的输入电压;Vd为PD的输出电压;Va为TWTA的输出电压;为求模运算。
令F[·]和G[·]分别表示PD和TWTA的复增益函数,则TWTA的输入-输出关系为
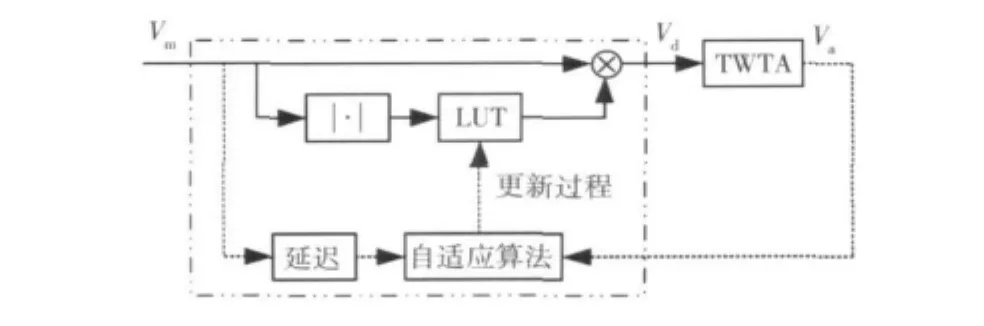
图3 自适应预失真器结构Fig.3 Architecture of adaptive predistorter

(6)式中,G[·]由(5)式计算。PD的输入-输出关系为

对任意输入电压,PD复增益函数F最佳值的选取依据是使预失真器和行波管放大器的联合幅度增益为常数K。将(7)式代入(6)式,PD和TWTA的联合响应为

(8)式可以化简为
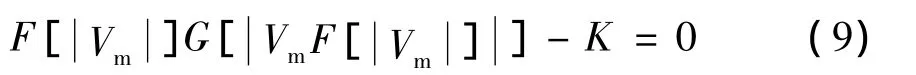
实际电路中,HPA的输入电压不会超过饱和电压,因此预失真器的输入范围为

(10)式中,1是对饱和输入电压的归一化值。设LUT的尺寸为N,LUT表的量化间隔为

将量化区间的中点作为表项索引,则每个LUT项的索引和表项值分别记为

(13)式中,i=0,1,…,N - 1 。
2 自适应预失真算法
为使预失真器能够自适应更新,定义代价函数为TWTA的输出与理想输出之间的误差,表示为

(14)式中,K为增益因子。在给定输入电压下,F的最优解是使(14)式最小的值。该过程可以通过非线性方程的求解实现,而定点迭代算法在非线性系统求解中应用广泛。
2.1 定点迭代算法
定义 设Ω表示规范空间X的闭集,φ表示Ω空间上的某种变换。若对任意x1,x2∈Ω,存在α(0≤α <1)使得‖φ(x1)-φ(x2)‖≤α‖x1-x2‖,则φ
根据压缩映射定理,将非线性方程f(x)=0,化为x=φ(x)的形式,得到定点迭代算法的迭代格式x(k+1)=φ(x(k))。根据(14)式,预失真器复增益函数最优值的查找需要求解方程E(F)=0,首先化为迭代式

(15)式中,φ为压缩映射。
将(14)式代入(15)式,不失一般性,假设增益因子K=1,预失真器的压缩映射φ可以记为

查找表的表项的更新可以通过(17)式获得。

(17)式中,Fi(k)表示查找表第i个表项的第k次迭代。一旦输入电压幅度进入某个量化区间,相应的表项值就被更新。被称为Ω上的压缩映射[12]。
压缩映射定理 如果φ是Ω上的压缩映射,则φ(x)在Ω上有唯一的不动点x*满足x*=φ(x*);对于任意初值x(0)∈Ω,由迭代格式x(k+1)=φ(x(k))产生的迭代序列收敛,即
2.2 Steffensen加速方法
多数情况下,定点迭代的收敛速度是线性的。为了提高迭代速度,可以采用Steffensen加速法[12]。将Steffensen加速应用于预失真器的迭代,则预失真器的迭代格式为
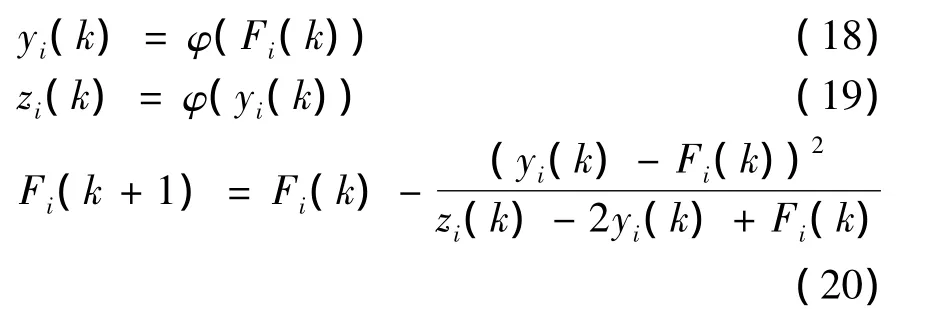
Steffensen加速法使迭代过程至少具有平方敛速,因而能够提高算法迭代的速度。另外,Steffensen加速技巧还可以使不收敛的过程收敛,提高了算法的稳定性。从(20)式可知,Steffensen算法每次迭代需要4次复数加法,1次复数乘法,1次实数和复数乘法,1次复数除法;在割线法中,每次迭代需要2次复数加法,2次复数乘法,1次复数除法。2种算法的计算量非常接近。
3 仿真结果与分析
针对16APSK系统对预失真算法的收敛速度和预失真效果进行了仿真和分析。仿真模型采用图1所示模型,调制器产生4+12-APSK信号,外圆半径和内圆半径比为2.732。发送滤波器和接收滤波器的滚降系数为0.35,过采样因子为8,持续时间为7个符号长度。
图4是不同算法的收敛曲线。图4a-4b中,TWTA的功率回退(input back off,IBO)分别是3.16 dB和0.49 dB。线性算法的初值和迭代因子分别为Fi(0)=0.5和μ=0.4;割线法的初值为Fi(0)=0.5,Fi(1)=1;本文提出的定点迭代算法初值为Fi(0)=0.5。从图4可见,无论是在饱和区还是线性区,定点算法的收敛速度都是最快的。
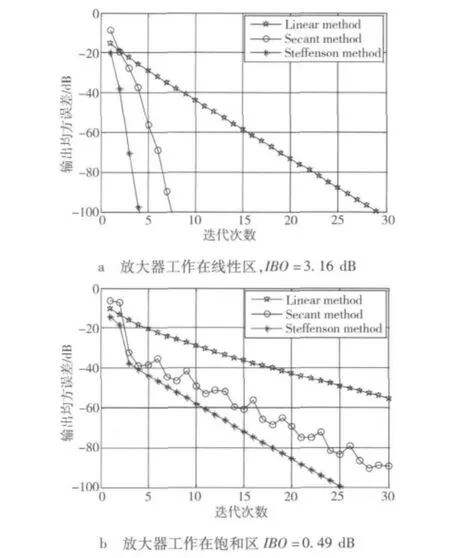
图4 不同算法的收敛速度比较Fig.4 Comparison of convergence rate
表1比较了不同条件下不同算法的迭代次数,表1中数据均在输出均方误差(output square error,OSE)达到-50 dB时得到。表格的第2,3列分别是TWTA工作在3.16 dB和0.49 dB的迭代次数;第4,5列在表格尺寸为64时对迭代的平均次数和总次数进行了统计。无论何种条件下,本文所提算法收敛次数都是最少的。

表1 不同算法的迭代次数比较Tab.1 Comparison of iteration times
图5a-5b是APSK信号的功率谱密度函数和星座图。信号通过信道后,高功率放大器的非线性特性使得信号的幅度和相位均有失真,并且产生了频谱扩展,造成邻信道干扰。使用预失真技术后,带外衰减达到-50 dB,比预失真前提高了25 dB,信号的幅度失真和相位失真也都得到矫正。

图5 预失真前后功率谱密度曲线和信号星座图Fig.5 PSD and signal constellation before and after predistorter
4 结束语
针对卫星通信系统中高功率放大器引起的非线性失真问题,在复增益结构的自适应基带预失真技术基础上,提出一种新的迭代方法,利用压缩映射原理,将预失真器查找表的更新看作定点迭代过程,并使用Steffensen加速技巧提高收敛速度。新算法使收敛阶数达到2以上,比线性法和割线法收敛速度更快;使系统的带外辐射降低到-50 dB以下,比预失真前降低了25 dB,同时克服了信号的幅度和相位失真;算法复杂度和广泛使用的割线法相当。
[1] SUNGW,KANG S,KIM P.Performance analysis of APSK modulation for DVB-S2 transmission over nonlinear channels[J].International Journal on Satellite Communications and Networking,2009,27(6):295-311.
[2]DING L.Digital predistortion of power amplifiers forwireless applications[D].Atlanta:Georgia Institute of Technology,2004.
[3] ZHOU Yu-guang,MCLANE P J,LOO C.Performance of predistorted APK modulation for one-and two-link nonlinear power amplifier satellite communication channels[J].IEEE Transactions on Vehiclar Technology,2005,54(2):629-638.
[4] GIUGNO L,LUISE M,LOTTICI V.Adaptive pre-and post-compensation of nonlinear distortions for high-level datamodulations[J].IEEE Transactions on Communications,2004,5(3):1490-1495.
[5]沈英杰,刘郁林,胡中豫.自适应数字预失真方法在功放线性化中的应用[J].重庆邮电大学学报:自然科学版,2005,17(6):1-5.
SHEN Ying-jie,LIU Yu-lin,HU Zhong-yu.Application of an adaptive digital predistortion technique to HPA linearization[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition.2005,17(6):1-5.
[6] FAULKNER M,JOHANSSON M.Adaptive linearization using predistortion-experimental results[J].IEEE Transactions on Vehiclar Technology,1994,43(2):323-332.
[7]CAVERS JK.Amplifier linearization using a digital predistorter with fast adaptation and low memory requirements[J].IEEE Transactions on Vehiclar Technology,1990,39(3):374-382.
[8] ANDREA A N D,LOTTICIV,REGGIANNINIR.Efficient digital predistortion in radio relay links with nonlinear power amplifiers[J].IEE Proceeding of Communications,2000,147(3):175-179.
[9]LIN Xiao-chen,JIN Ming-lu,LIU Ai-fei.A discrete newton'smethod for gain based predistorter[J].International Journal of Communications,Network and System Sciences,2008,1(1):16-21.
[10]HUSSEIN M A,WANG Y D,FEUVRIE B.LUT/Parametric digital predistortion approach for the linearization of power amplifiers characteristics[C]//IEEE.Proceeding of the 38th European Microwave Conference.New York:IEEE Press,2008:571-574.
[11] SALEH A A M.Frequency-independent and frequency-dependent nonlinearmodels of TWT amplifiers[J].IEEE Transactions on Communications.1981,29(11):1715-1720.
[12] KELLEY C T.Iterative methods for linear and nonlinear equations[M].Philadelphia:Society for Industrial and Applied Mathematics,1995:65-70.

