基于效用函数的C+W 网络负载均衡研究
张 宝,向 阳,张 锐
(中国电信股份有限公司四川分公司无线网络优化中心,四川成都 610091)
0 引言
随着无线宽带业务的逐步成熟和应用,用户对网络资源及服务质量的需求日益增加,这就要求网络运营商必须有效地提高现有网络资源的利用率,实现利益的最大化。负载均衡就是在这种背景下提出的一种能够优化网络资源,实现CDMA与WIFI,WIFI与WIFI之间的自动无缝切换,提高网络性能的有效技术。在无线宽带网络中,C+W负载均衡技术的核心是使CDMA与WIFI共存的无线接入网络成为一个具有网络资源管理和网络资源优化的网络。
针对负载均衡问题,文献[1]提出了一种基于接入用户数及无线网络环境的门限切换方法。文献[2]提出了基于博弈论的多主接入网络负载均衡方法。
如何有效地分配有限的资源,从而最大限度地实现资源的潜在价值,这正是经济学研究得比较成熟的问题。本文针对CDMA 2000和WIFI混合组网下的负载均衡问题,将经济学中的博弈理论应用到切换策略中,提出了一种基于博弈论的解决方案。
1 C+W网络负载均衡和博弈论
1.1 C+W网络负载均衡
C+W网络是指一个移动设备能够同时连接到CDMA2000和WIFI 2个无线移动网络中进行通信,如图1所示。对于融合多个接入网络的异构系统,由于用户对网络的选择会随着时间地点的差异而不同,另外业务类型方面的考虑也会促使用户自由选择不同的网络。这种选择标准的多样性通常使网络选择和带宽分配有很大的随机性。如何在多个网络之间实现合理的资源分配,使之不至于使某一网络超载,而另一网络未能充分发挥处理能力的情况。负载均衡就是在这种背景下提出的一种策略或机制,它建立在网络结构之上,能以较低成本消除网络瓶颈,有效解决网络拥塞问题,提高网络频谱、信道资源的利用率,从而为用户提供更好的服务。
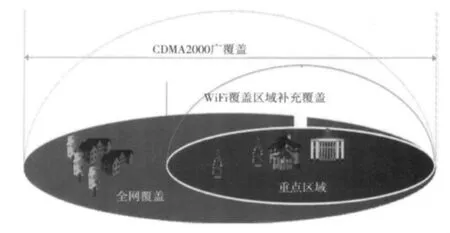
图1 C+W网络覆盖Fig.1 Network coverage of C+W
1.2 博弈论
博弈论(game theory)又称对策论,是专门研究2个或2个以上利益有冲突的个体,在有相互作用的情况下,如何进行各自优化决策的理论。一般而言,经典博弈论包括三要素:参与者(player)、策略(action)、收益(utility)。博弈论就是系统研究用合理方法定义的各种各样的博弈问题,寻求各博弈方合理选择策略的情况下博弈的解,也既是均衡。
2 基于博弈论的C+W网络负载均衡
2.1 用博弈论分析C+W网络负载均衡
用博弈理论研究C+W网络负载均衡问题,即解决在CDMA2000和WIFI 2个无线移动网络共同存在的状态下,如何通过制定合理的策略(博弈均衡解)使得系统总效用最大化的问题。
在C+W网络中,不同的接入网络构成博弈中的“参与者”,不同的接入网络选择不同策略进行网络资源分配的过程就是“参与者”进行博弈的过程。运用博弈思想,不同网络灵活调整网络资源分配策略,在获得最优策略时,负载的均衡分布也使得系统中各网络的资源得以均衡利用。微观经济学理论证明:当系统处于均衡状态时,资源配置是最优的,系统总效用最大。
2.2 博弈模型的建立与分析
设CDMA网络以pc的单位网络资源虚拟定价向用户提供bc的带宽,其支出的成本为Cc,同理WIFI网络以pw的单位网络资源虚拟定价向用户提供bw的带宽,其支出的成本为Cw,策略管理单元依据无线环境、业务类型、带宽需求等条件来均衡各网络之间的负载情况,由此,建立了如图2所示的C+W网络负载均衡模型。

图2 C+W网络中负载均衡模型Fig.2 System model for load balancing in C+W network
定义1 效用函数u是一个从策略集合S到实数集合R的一个映射,记为:u:S→R,如果对于所有x,y∈S,当且仅当u(x)≥u(y)时,策略x比策略 y的满意度高[3]。
在博弈理论中,效用函数应反映博弈者对选择某一策略后所得到结果的满意程度。在C+W网络中,用户的满意程度应根据数据业务的质量来确定。因此,在无线网络资源中,效用函数应该用来评估用户对网络服务质量的满意度。
通常情况下,用户对某一网络的需求情况直接反映了用户对该网络的满意程度(用户对网络的满意度越高,其对该网络的需求也就越大),而用户对网络带宽的需求情况与所有网络能够提供的带宽、单位带宽的定价、以及传输信息的误码率、信噪比等有关系。另外,单位网络资源虚拟定价与“市场上”网络提供方的竞争程度有密切关系。网络提供方相互之间竞争得越激烈,单位带宽的定价就会被压得越低,而作为用户方是从中收益的。用户总是希望耗费最少的代价获得最大的效用。综合上述分析,用户对带宽需求的效用函数应满足以下几点性质。
1)当网络所提供的带宽一定时,效用函数应该是价格的单调减函数;
2)当价格一定时,效用函数应该是网络所提供的带宽的凸函数;
3)当单位网络资源虚拟定价趋于0时,效用函数应趋于无穷大;
4)当网络所提供带宽接近0时,效用函数亦应趋于0;
5)应能描述无线环境(传输信息的误码率、信噪比、时延等)下,系统的服务质量。
如上所述,为量化用户对带宽的需求,需要建立满足上述性质的效用函数。本节以N.Singh和X.Vives的垄断市场中价格与产量之间均衡的效用函数为基础,并对其进行改进得到一个新的、适用于C+W网络的负载均衡效用函数。在引入新的效用函数之前,有必要先给出N.Singh和X.Vives的效用函数为[4]

(1)式中:n=1,2;qi为垄断市场中博弈者i的产量;pi为博弈者 i的定价;αi,βi为常数,且 αi,βi>0;γ反映博弈者生产的产品之间的可替代性(即博弈者i的产品质量或其所提供的服务与其他博弈者之间的差异性),γ∈(0,1.0)。相对其他效用函数,该二次效用函数具有以下优点,首先,它是凸函数,因此可以描述用户的满意饱和度。凸效用函数在量化带宽分配的用户满意度上得到了广泛的应用。其次,对该函数求导以后得到的用户需求函数是线性的,从而降低分析难度。
该效用函数映射到无线数据通信系统,网络所提供的带宽即为垄断市场中博弈者的产量,带宽的虚拟定价即为博弈者的定价。博弈者生产的产品之间的可替代性,即为各网络提供方之间竞争的激烈程度,因为当某一产品能够被同类产品自由替换,说明他们提供的服务和功能是完全相似的,也就意味着竞争就越激烈。另外,用户对带宽需求的效用函数还应该包含反映信道传输质量的误码率、信噪比、时延等重要指标。这里,我们引入频谱传输效率α。在无线通信系统中,信息的传输效率跟信道的传输质量有直接关系,而信道传输信息的误码率和信噪比是信道传输质量的重要指标。为不失一般性,这里考虑采用自适应多阶正交幅度调制(multiple quadrature amplitudemodulation,MQAM),系统所采用的信道为高斯噪声信道。该环境下信道的比特误码率(BER)约为

(2)式中:γ为接收者的信噪比(SNR);α为频谱效率[4]。为保证信息的传输质量,通常情况下BER要控制在一定的范围,信道的信噪比γ(SNR)是用户已知的。因此,网络i的频谱传输效率为

经过上述转换,将N.Singh和X.Vives提出的效用函数改写为(4)式,该效用函数既完全符合上述效用函数的性质,又可以很好地表示用户的满意度。

(4)式中:αc,αw分别为CDMA网络与WIFI网络的频谱传输效率;βc,βw分别为反映 CDMA网络与WIFI网络的时延参数;参数 λ是 CDMA网络与WIFI网络之间在不同业务类型下的可替换性,定义λ∈(-1.0,1.0)。
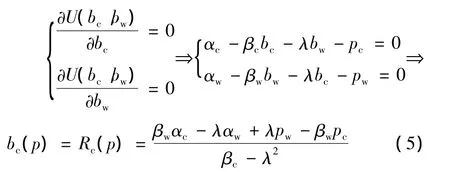
同理可得,WIFI网络的带宽需求Rw(p)。
在模型中,某一网络i的收入Ei=pibi,成本Ci(b)=ciαibi。其中,ci为单位成本支出;αi为网络i的频谱传输效率;bi为用户对网络的需求Rc(p)。因此,网络i的收益函数表示为

(6)式中,Ri(p)为网络i的带宽需求。
对于同时拥有CDMA网络和WIFI网络运营商而言,追求的是2个网络的收益和Ptot,其中Ptot为

(7)式中:Pc为CDMA网络收益,Pw为WIFI网络收益。
对博弈模型的求解过程就是求Nash均衡解的过程。Nash均衡策略[6]是指:无论其他参与者如何改变策略,该参与者的效益不可能再增加。本文通过对CDMA网络的最佳响应函数求解,可得Nash均衡解,即CDMA网络在获得最大收益时的单位网络资源虚拟定价,同理可获得WIFI网络在获得最大收益时的单位网络资源虚拟定价。
由用户获得最佳满意度时,带宽需求与网络资源虚拟定价之间的关系,可得最佳带宽分配方案为
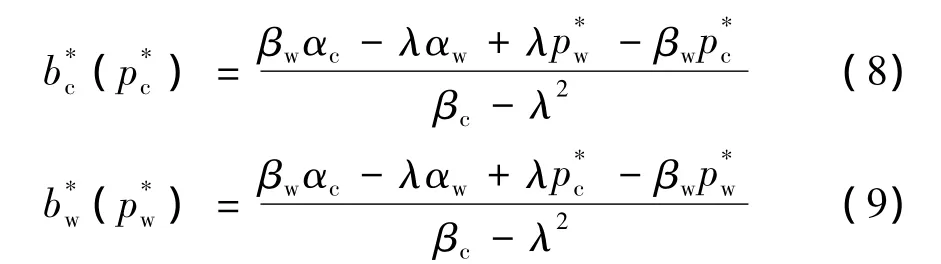
通过求解得
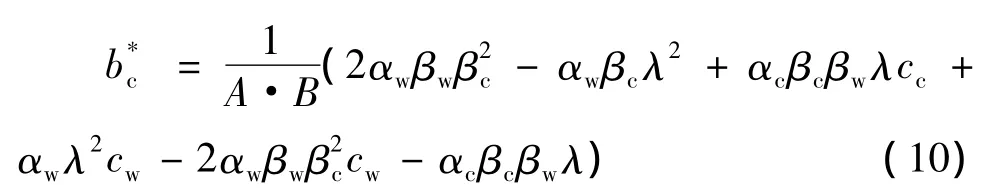
(10)式中:A=4βcβw-λ2;B=βw-λ2。同理可得。
由此可见,当获知网络的比特误码率、信噪比、网络时延、业务类型及成本后,即可得出网络带宽的最佳分配策略。
对于同时拥有CDMA网络和WIFI网络运营商而言,追求的是2个网络的利益和最大化。因此,可通过上述方法求得的解,即使网络整体最优的解,从而保证网络整体利益最大化。
3 C+W网络负载均衡实现流程
C+W网络的负载均衡具体实现流程如图3所示。首先由用户提交接入申请,在接受到申请以后判断无线环境中是否存在多个接入网络,该判断存在4种情况:1)仅有CDMA接入网络,则进行C网的单一网络接入认证并接入CDMA网络;2)仅有WIFI接入网络,则进行W网的接入认证并接入WIFI网络;3)无可用接入网络,给出提示信息;4)CDMA网络与WIFI网络均可接入,此时由无线上网终端获取信噪比、误码率、业务类型等重要关键指标,依据上述指标采用博弈负载均衡算法制定出最优带宽资源分配方案,最终选择最优策略的接入网进行认证并接入。上述流程完成了单一用户的接入,当有后续用户接入时,无线环境及带宽可用资源已发生变化,系统将在不中断已接入用户服务的基础上依据上述流程,选择最大化当前效用的最优策略接入。依据上述流程,实现了C+W网络的带宽资源的高效利用,提升了用户感知度,进而实现了网络运营商的利益最大化。

图3 C+W网络负载均衡实现流程图Fig.3 Flow chart of C+W network load balancing
4 仿真结果及分析
仿真中,参数设置如下:高斯信道中比特误码率BER在0.000 1~0.001之间,信噪比(SNR)γ在10~20 dB之间,网络时延β在10~100 ms之间,CDMA网络与WIFI网络之间在不同业务类型下的可替换性λ∈(-1.0,1.0)。
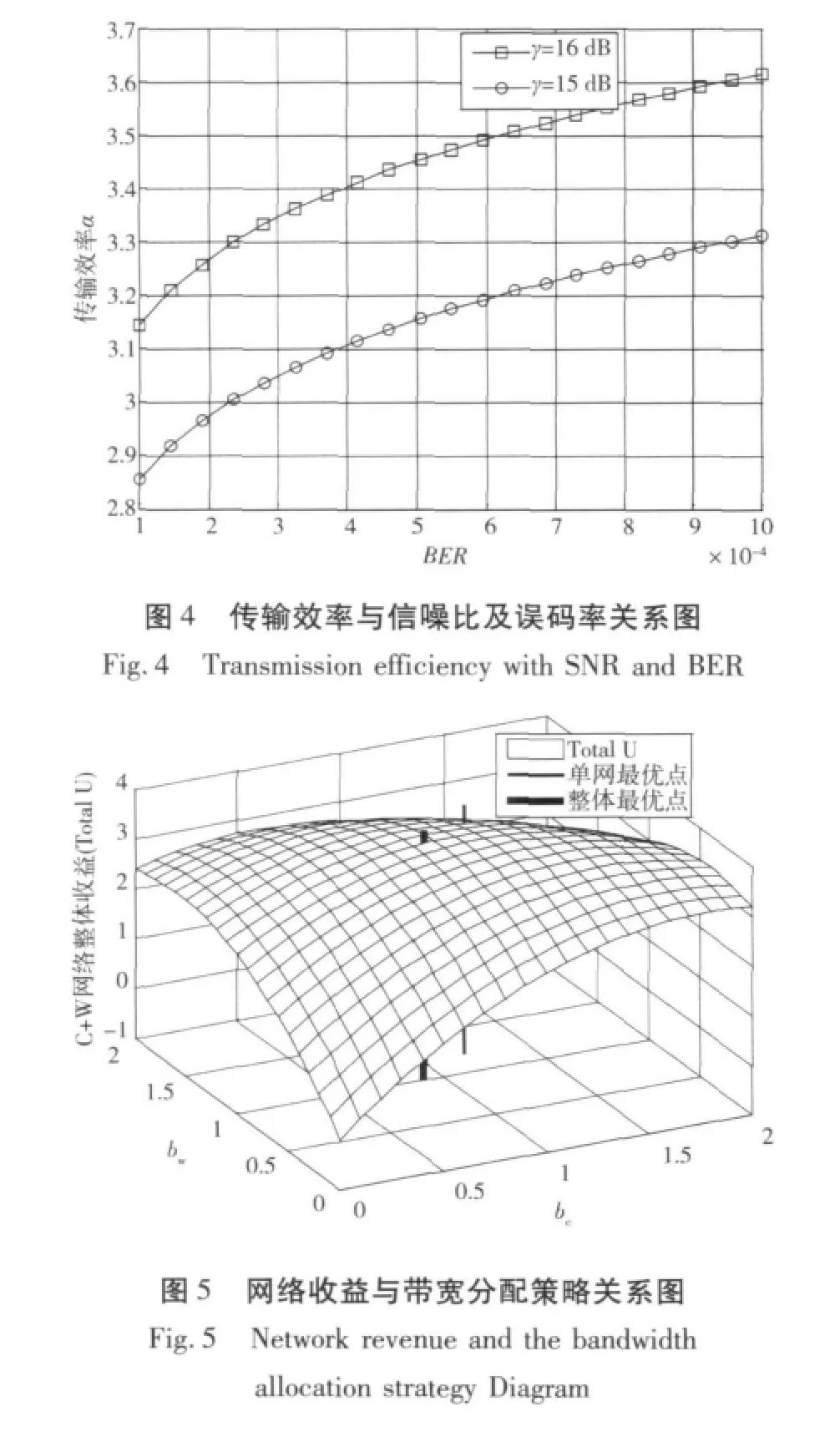
图4描述了频谱的传输效率与误码率及信噪比之间的关系。误码率不变的情况下,当信噪比提高时,信道的传输效率随之增加,反之,当信噪比一定的情况下,当误码率减小时,信道的传输效率将有所下降,这是由于信息传输的有效性和可靠性是矛盾统一的,因此通常需要根据实际业务需求有所侧重。观察到,当误码率增大到一定范围后,传输效率提高的速度有所下降,这说明当信道误码率增大到一定程度后,对于提升信道传输效率的影响将随之减弱,而随着信噪比的增大,信息传输效率提升的速度也随之加快,因此,可以在满足一定可靠性指标下,尽量通过增加信道的信噪比提高消息的传输速度。
图5为运营商总体网络收益与带宽分配策略关系图,其中纵坐标Total U为C+W网络整体收益。从图5中可以看出,在无线环境一定的情况下,特定的带宽分配方案能够给C+W网络带来最大收益,即我们追求的最佳策略。对于单独的CDMA网络或者WIFI网络而言,单网最优点保证了该网络在此刻获得最大的收益,但对于同时拥有CDMA网络与WIFI网络的运营商而言,则不能满足总体最优。在整体最优点则保证了网络整体收益的最大值,这也是负载均衡的最佳带宽分配方案点。对于单个网络都是“理性”的,它会主动追求自身最大收益而忽略整体收益,这种适合于非合作的竞争,作为同时拥有2个网络的运营商而言,可以通过建立一个“长效机制”共同合作来获得C+W整体网络的最大收益。
5 结论
负载均衡对于提高网络性能,保证业务QoS,提升用户感知度是非常重要的。本文利用博弈模型解决了C+W网络的负载均衡问题,梳理了负载均衡实现的流程,实现了网络资源的合理利用。仿真结果表明,在无线环境一定的情况下,某一特定的带宽分配方案能够给C+W网络带来最大收益。
[1]LIU J,JIN X,WANG Y.Agent-based load balancing on homogeneous minigrids:macroscopic modeling and characterization[J].IEEE Transactions on Parallel and Distributed Systems,2005,16(7):586-598.
[2]陈前斌,张宝,唐伦,等.基于 Stackelberg博弈论的Multi-Homing负载均衡研究[J].计算机科学,2009,36(5):76-78.
CHEN Qian-bin,ZHANG Bao,TANG Lun,et al.Research on load balancing Based on Stackelberg game theory for Multi-Homing in Heterogeneous Wireless Networks[J].COMPUTER SCIENCE 2009,36(5):76-78.
[3] 约翰·纳什.纳什博弈论论文集[M].张良桥,王晓刚,译.北京:首都经济贸易大学出版社,2000.
NASH John Jr.ESSAYSON GAME THEORY by JOHN F NASH JR[M].ZHANG Liang-qiao,WANG Xiaogang,translation.Beijing:Capital University of Economics& Business Press,2000.
[4]SINGH N,VIVES X.Price and quantity competition in a differentiated duopoly[J].RAND JEconomics,1984,15(4):546-554.
[5] NIYATO D,HOSSAIN E.A Game-Theoretic Approach to Competitive Spectrum Sharing in Cognitive Radio Networks[C]//IEEE.IEEE Wireless Communications and Networking Conference.Hong Kong:IEEE Press,2007:11-15.
[6]NIYATO Dusit,HOSSAIN Ekram.Competitive pricing for spectrum sharing in cognitive radio networks:dynamic game,inefficiency of Nash equilibrium,and collusion[J].IEEE Select Areas Common,2008,26(1):192-202.

