采用GPS和水压测深法进行整平机框架定位测量及变形修正方法
李增军,张学俊,陆连洲
(1.中交第一航务工程局有限公司,天津 300461;2.中交一航局第二工程有限公司,山东 青岛 266071)
0 引言
深水抛石整平船青平2号的整平机采用框架结构,框架的定位测量决定整平区域平面位置和标高。在离岸深水港抛石基床整平关键技术研究课题研发过程中对框架定位测量方法进行了大量研究和论证,并确定了采用水压传感器进行水深测量和高程传递的方案。但是采用GPS和水压传感器可有多种不同的实施方案。通过对比最终确定了如下方案:框架定位采用2个GPS流动站来测定框架方位角,并给出平面位置和高程的起算点;采用4只水压传感器(sensor)测定框架纵倾和横倾角度,从而确定框架在工程坐标系中的位置。
由于框架具有一定柔性,在抛石基床顶面不平的情况下会产生扭曲变形。因而不能看作一个刚体来计算上面各点的坐标,而必须进行变形修正。
1 定位测量计算方法
1.1 框架及坐标系
整平机框架结构较复杂,为更清晰地表现各被测点相对位置关系,将其简化为图1所示的框架。框架坐标系与工程坐标系的关系见图2。
图2中,X、Y、Z为沿框架坐标轴X、Y、Z方向的单位线段的端点;T、A、B分别为由于框架坐标系转动所形成的框架Y轴在工程坐标系的xoy平面内的投影与工程y轴的夹角(顺时针为正)、框架X轴与工程坐标系的xoy平面(水平面) 的夹角(简称纵倾角,艏高艉低为正)、框架Y轴与工程坐标系的xoy平面(水平面)的夹角(简称横倾角,右舷侧高左舷侧低为正);Tx、Tz分别为框架X轴和Z轴在工程坐标系的xoy平面内的投影的补偿角(分别以逆时针和顺时针为正),其含义为:假定框架坐标系转动分三步完成,其顺序为先绕Z轴转动T,再绕Y轴转动A1(此时框架X轴在水平面内的投影为OU,框架Z轴在水平面内的投影为OW,两者处同一直线且与框架Y轴垂直,参见图2),最后再绕OU转动B。在形成夹角B的最后一步转动过程中,框架X轴和Z轴在工程坐标系的xoy平面内的投影会绕O点分别产生一个转角即所谓的框架X轴和Z轴在工程坐标系的xoy平面内的投影的补偿角。
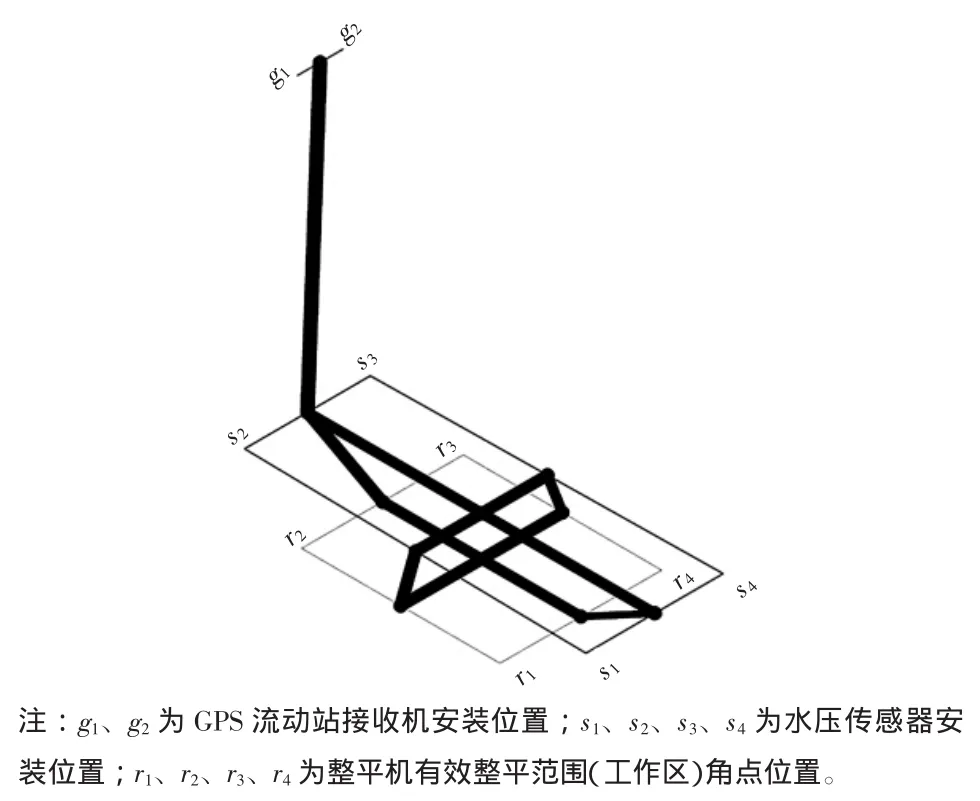
图1 GPS、水压传感器和工作区角点相对位置示意图
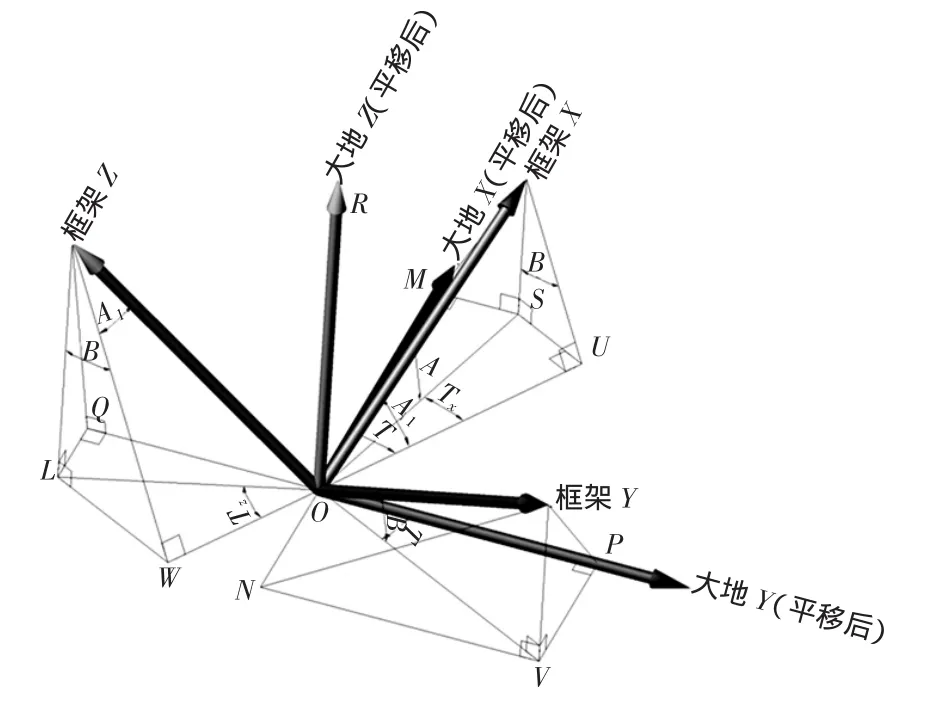
图2 框架坐标系与工程坐标系关系图
为方便计算,将各点的坐标(小写字母)组成矩阵,用各点名称所对应的大写字母表示如下:
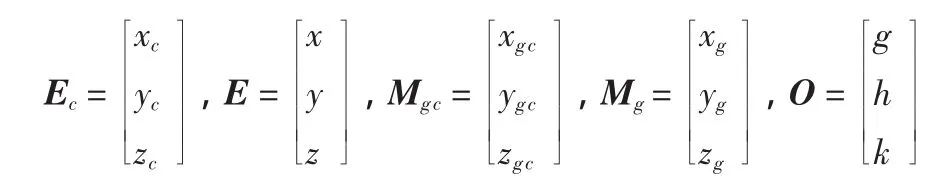
其中:ec(xc,yc,zc)为框架上任意点在框架坐标系中的坐标;e(x,y,z)为框架上任意点在工程坐标系中的坐标;mgc(xgc,ygc,zgc)为框架 GPS1—GPS2连线中点在框架坐标系中的坐标;mg(xg,yg,zg)为框架GPS1—GPS2连线中点在工程坐标系中的坐标;o(g,h,k)为框架坐标系原点的工程坐标。
根据上述定义,显然有:
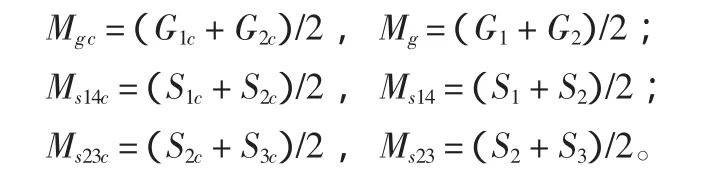
其中:g1(x1,y1,z1)为框架 GPS1在工程坐标系中的坐标;g2(x2,y2,z2)为框架GPS2在工程坐标系中的坐标;g1c(x1c,y1c,z1c)为框架GPS1(左舷侧) 在框架坐标系中的坐标;g2c(x2c,y2c,z2c)为框架GPS2(右舷侧)在框架坐标系中的坐标;s1c(xs1c,ys1c,zs1c)为框架sensor1在框架坐标系中的坐标;s2c(xs2c,ys2c,zs2c)为框架sensor2在框架坐标系中的坐标;s3c(xs3c,ys3c,zs3c) 为框架 sensor3在框架坐标系中的坐标;s4c(xs4c,ys4c,zs4c)为框架 sensor4在框架坐标系中的坐标;s1(xs1,ys1,zs1)为框架sensor1在工程坐标系中的坐标;s2(xs2,ys2,zs2)为框架sensor2在工程坐标系中的坐标;s3(xs3,ys3,zs3)为框架sensor3在工程坐标系中的坐标;s4(xs4,ys4,zs4)为框架sensor4在工程坐标系中的坐标;ms14c(x14c,y14c,z14c)为框架sensor1—sensor4连线中点在框架坐标系中的坐标;ms14(xs14,ys14,zs14)为框架sensor1—sensor4连线中点在工程坐标系中的坐标;ms23c(xs23c,ys23c,zs23c)为框架sensor2—sensor3连线中点在框架坐标系中的坐标;ms23(xs23,ys23,zs23)为框架sensor2—sensor3连线中点在工程坐标系中的坐标。
1.2 转角T
可根据GPS1和GPS2的实时坐标,按不同的象限分别计算:
假如x1≥x2,且y1<y2,则转角T处第一象限:

式中:g1(x1,y1,z1)为框架GPS1在工程坐标系中的坐标;g2(x2,y2,z2)为框架GPS2在工程坐标系中的坐标;g1c(x1c,y1c,z1c)为框架GPS1(左舷侧) 在框架坐标系中的坐标;g2c(x2c,y2c,z2c)为框架GPS2(右舷侧)在框架坐标系中的坐标。
1.3 框架纵、横倾角的确定
相对于艏横梁而言,矩形框架的扭曲实质上是左右两根纵梁绕艏横梁的型心纵轴(由梁横断面型心连线形成的直线)的转动,左右两纵梁的转角大小相等,方向相反。根据变形相容条件,两根纵梁绕艏横梁的纵向型心轴的转动会造成艏横梁的绕其型心纵轴扭转,艏横梁左右两端的横断面绕其型心的转角分别与左右纵梁绕艏横梁的型心纵轴的转角相等,而艏横梁的长度中点处的横断面绕自身型心的转角为零。在这种状态下,由于GPS1和GPS2的安装塔架的型心纵轴与艏横梁型心纵轴垂直相交于后者的中点处,因此它不会由于框架扭曲而绕艏横梁的型心纵轴转动。同时,由于左右两纵梁的转角大小相等方向相反,艉横梁型心纵轴的中点与艏横梁型心纵轴的中点的连线不会因为框架扭曲而产生绕艏横梁型心纵轴的转动。这就是说,艏横梁的型心纵轴、GPS安装塔架的型心纵轴和艉横梁型心纵轴的中点与艏横梁型心纵轴的中点的连线之间的相对位置关系不因框架扭曲而改变。为此,采用艏横梁型心纵轴与水平面的夹角作为框架坐标系Y轴同水平面的夹角B,采用艉横梁型心纵轴的中点与艏横梁型心纵轴的中点的连线同水平面的夹角作为框架坐标系X轴同水平面的夹角A,这样所确定的框架坐标轴与艏横梁的型心纵轴、GPS安装塔架的型心纵轴之间的相对位置关系不因框架的扭曲而发生改变,从而最大限度地消除框架扭曲造成的框架上各点平面定位的误差。
由于sensor2和sensor3安装于艏横梁上,两者连线同水平面夹角的改变等于艏横梁型心纵轴同水平面夹角的变化,为此可采用sensor2和sensor3测得的水深数据和两者在框架坐标系中的坐标计算横倾角B,计算公式如下:
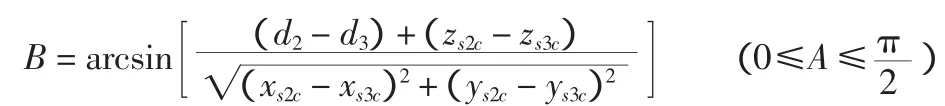
由于sensor2、sensor3和sensor1、sensor4分别安装于艏、艉横梁上,且sensor2—sensor3连线中点和sensor1—sensor4的连线中点分别靠近艏、艉横梁型心纵轴的中点,且4点基本处于同一个平行于框架Z轴的平面内,因此可采用sensor2—sensor3的连线中点和sensor1—sensor4的连线中点在框架坐标系中的坐标值和水深数据计算框架X轴同水平面的夹角A,计算公式如下:
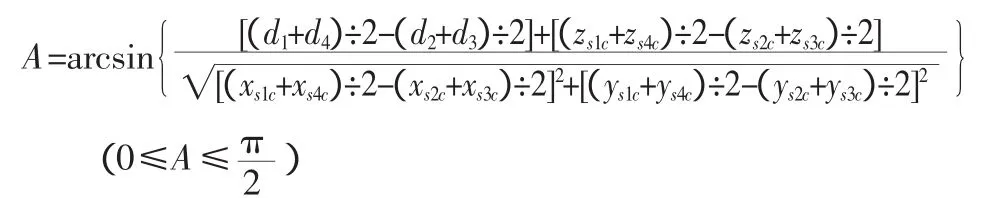
式中:d1、d2、d3、d4分别为传感器 sensor1、sensor2、sensor3和sensor4所测水深;s1c(xs1c,ys1c,zs1c)为框架sensor1在框架坐标系中的坐标;s2c(xs2c,ys2c,zs2c)为框架sensor2在框架坐标系中的坐标;s3c(xs3c,ys3c,zs3c)为框架sensor3在框架坐标系中的坐标;s4c(xs4c,ys4c,zs4c)为框架 sensor4在框架坐标系中的坐标。
1.4 框架X轴和Z轴投影补偿角
按照上述定义和各点几何关系,可得X轴和Z轴投影补偿角计算公式如下:
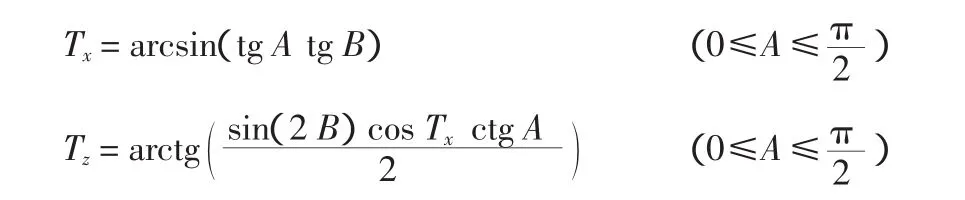
1.5 框架坐标轴在工程坐标系中的方向余弦
按照上述定义和各点几何关系,可得方向余弦计算公式。
框架坐标轴OX的方向余弦:

式中:φx、φy、φz分别为框架X轴正方向同工程x、y、z轴正方向的夹角;ψx、ψy、ψz分别为框架Y轴正方向同工程x、y、z轴正方向的夹角;Ωx、Ωy、Ωz分别为框架Z轴正方向同工程x、y、z轴正方向的夹角;l1、m1、n1分别为框架X轴正方向同工程x、y、z轴正方向夹角的余弦;l2、m2、n2分别为框架Y轴正方向同工程x、y、z轴正方向夹角的余弦;l3、m3、n3分别为框架Z轴正方向同工程x、y、z轴正方向夹角的余弦。
1.6 框架坐标原点在工程坐标系中的坐标
确定了框架坐标轴在工程坐标系中的方向之后,要完全确定其位置,需求出其坐标原点的工程坐标o(g,h,k)。
如前所述,框架坐标轴与GPS安装塔架的型心纵轴之间的相对位置关系不因框架的扭曲而发生改变,而GPS1—GPS2连线的中点位于塔架型心纵轴上,故GPS1—GPS2连线的中点在框架坐标系中的位置不受框架扭曲的影响。因此,可以该点为根据定位框架坐标系原点的工程坐标。根据坐标系旋转平移公式得:

2 框架变形偏差的校正
2.1 框架上某点e(x,y,z)的工程坐标及传感器高程的矫正
根据坐标系旋转平移公式得:

根据该式,可计算出传感器sensor1、sensor2、sensor3和sensor4的工程坐标和有效整平区域4个角点r1、r2、r3和r4的工程坐标。
请注意,尽管在前述计算中最大限度地避免了框架扭曲造成的各点平面定位误差,但是扭曲给各点高程计算结果造成的误差是不可忽略的,必须加以矫正。由于如前所述,框架坐标轴与艏横梁的型心纵轴之间的相对位置关系不因框架的扭曲而发生改变,且框架横倾角是依据sensor2和sensor3的位置和水深数据确定的,因此该两只传感器的高程不需要矫正;sensor1和sensor4的高程可依据所测水深数据计算如下:
首先计算潮位,取sensor2和sensor3所测潮位的平均值作为最终结果:
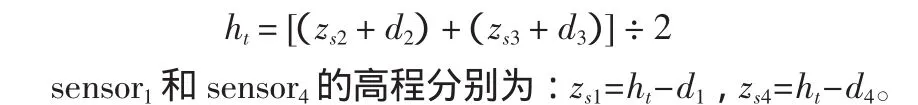
2.2 有效整平区域角点高程的矫正
由于r1和r2位于左纵梁上,r3和r4安装于右纵梁上,因此,可分别将左、右纵梁同水平面的夹角Al、Ar作为框架坐标轴X同水平面的夹角,按照前述方法对框架坐标系进行定位,计算得到两套坐标轴方向余弦和坐标系原点,分别用于计算r1、r2和r3、r4的高程。即令A=Al计算zr1和zr2,令A=Ar计算zr3和zr4,作为有效整平区域4个角点高程的最终结果。
显然,由sensor1—sensor2—sensor3连线构成的平面,和sensor2—sensor3—sensor4连线构成的平面相交于sensor2—sensor3的连线,两平面形成一个夹角αs。由于sensor2—sensor3和sensor1—sensor4分别安装于艏、艉横梁上,靠近左、右纵梁的前、后两端,在可接受的误差范围内,按照几何比例,夹角αs与左、右纵梁之间的夹角αr之间有如下关系:
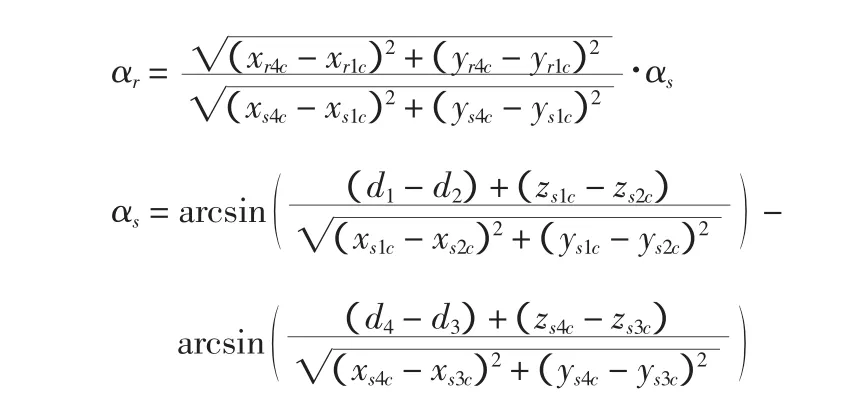
由此可计算出左、右纵梁型心纵轴与同时包含艏横梁型心纵轴和艏、艉横梁型心纵轴中点连线的平面之间的夹角分别为:
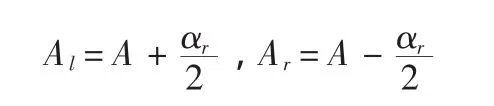
令 A=Al计算 zr1和 zr2,令 A=Ar计算 zr3和 zr4,作为有效整平区域 4 个角点(见图 1,r1、r2、r3、r4)高程的最终结果。
3 结语
上述成果已经应用于青平2号的压力传感器测量系统中,形成了一套完整的水下定位测量新方法。采用GPS通过拉线法直接测定框架角点高程,并与采用GPS和水压测深法进行整平机框架定位的测量结果进行了对比。通过对比,验证了这一新的测量方法的正确性和实用性,类似工程可参考使用。
[1] 刘和祥.基于传感器信息的AUV局部避碰研究[J].传感器与微系统,2007,26(12):41-43.
[2]喻志发.从实测数据判断箱筒型结构在风浪作用下的稳定性[J].中国港湾建设,2010(2):21-24.
[3]赵晓龙.RTK与测深联合技术及其在近海工程勘查中的应用[J].海岸工程,2007,26(3):15-17.

