基于量子遗传算法的TDOA定位技术研究＊

王 迅 吴 涛

（91404部队93分队 秦皇岛 066001）

1 引言

随着移动通信技术的飞速发展，利用蜂窝网络对移动台进行定位将逐渐成为蜂窝网络的一项重要功能。近年来无线通信基本的定位技术包括场强定位法、基于电波传播时间（TOA）或时间差（TDOA）的定位法、来波角度定位法（AOA）以及各类混合定位法。其中，TDOA定位法通过电波从移动台（MS）传播到多个基站（BS）的传播时间差来确定移动台的位置，该方法由于对设备改动少并且不需要移动台基站间进行严格的同步，因而是一种理想的定位方法。

对于TDOA方式，若多个接收机位于一条直线上，有许多优化处理方法。但如果接收机在空间随机分布，在求解双曲线方程组时会遇到非线性问题。文献［3］给出了采用傅里叶级数的迭代算法，这种迭代需要一个较好的初始值，否则容易落入局部最小点，而且不保证收敛；文献［4］提出了一种两步加权LS方法，在误差很小的情况下，性能逼近最优值，但是这种方法由于引入了测量参数的平方项，当测量误差较大时，噪声的二次项不可忽视；文献［5］采用遗传算法解极大似然函数，通过合理设置种群规模以及变异率，能找到逼近全局最优点的解相对于其它算法精度高，但由于计算量大，实时实现很困难。

本文提出一种结合Chan算法和量子遗传算法的TDOA定位算法，该算法首先根据移动台所在的服务区扇区来确定移动台坐标范围，然后采用似然函数的倒数作为目标，通过迭代，在确定的坐标范围内进行搜索。仿真结果说明，通过合理设置量子旋转门，能得到较高精度的解。

2 TDOA 双曲线数学模型［1，3～5］

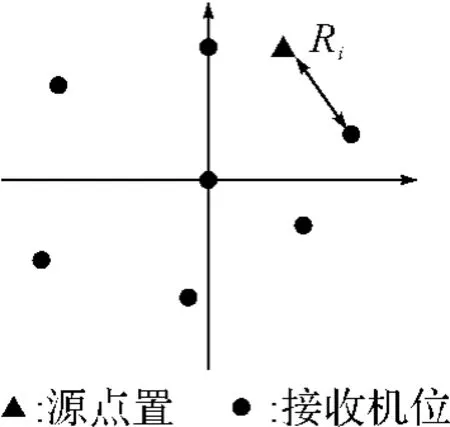
图1 二维平面示意图

如图1所示，假设M个接收机分布在二维平面上，（x，y）为移动台的待估位置，（xi，yi）为第i个基站的已知位置。移动台到基站i的距离为Ri，令R0i，1表示移动台与基站i（i≠1）和基站1（服务基站）的实际距离差，测量值记作为Ri，1，则

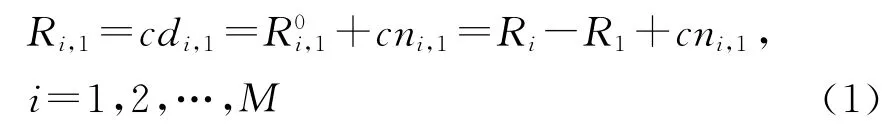
式中：c为电波传播速度；di，1是 TDOA 测量值；ni，1是测量TDOA时引入的噪声，为方便起见，可认为是独立同分布的方差为σ2的高斯白噪声。

又因为

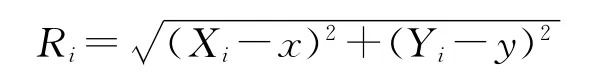
所以有

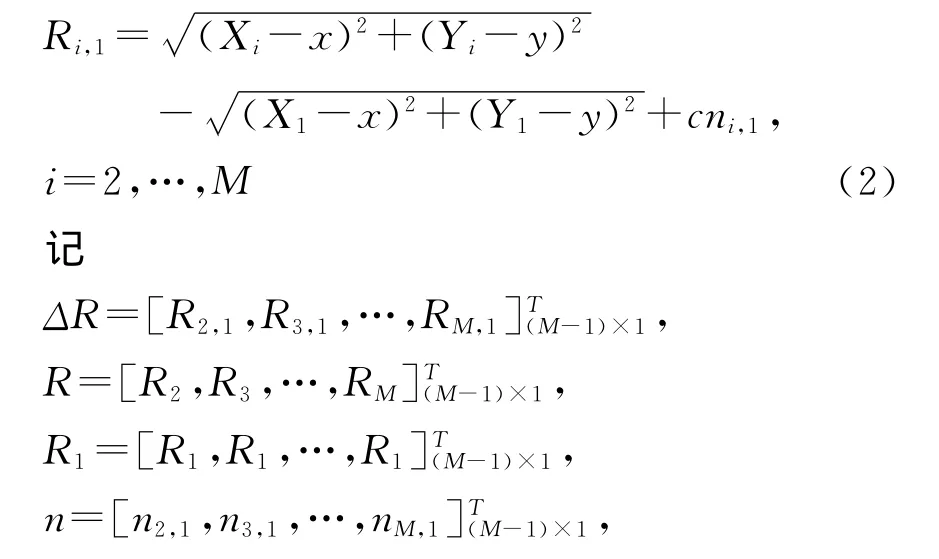
可得

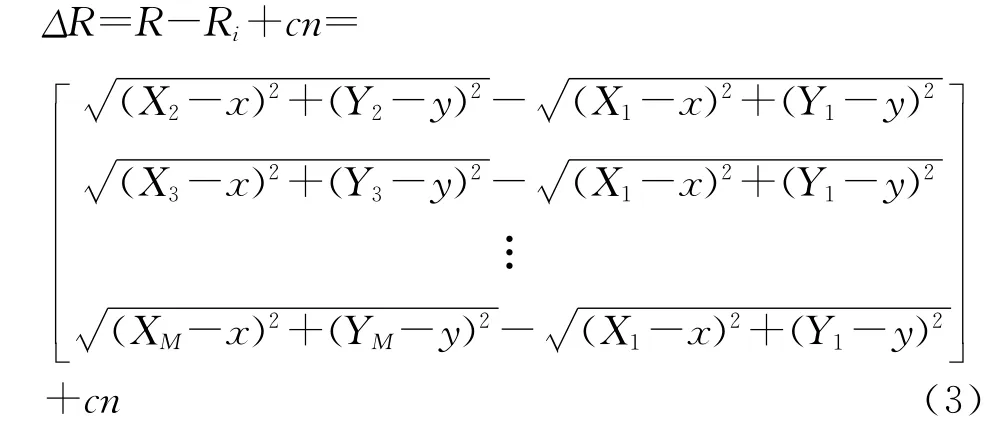
文中考虑M＞3时的情况，采用最大似然法估计源点坐标（x，y）。因为Ri，1服从均值为（Ri－R1），方差为σ2的高斯分布，因各测量值独立，则似然函数为

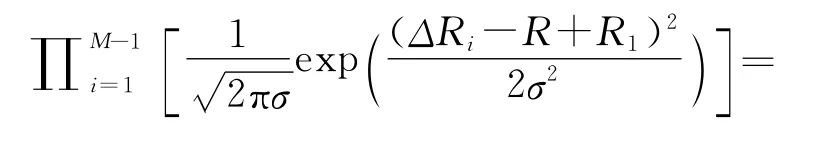
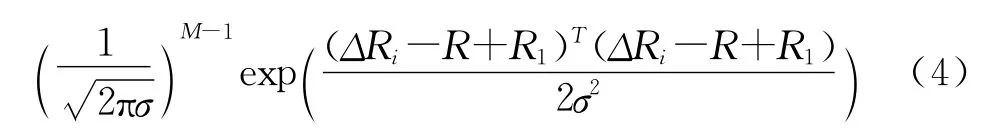
求使似然函数最大的坐标值，相当于求

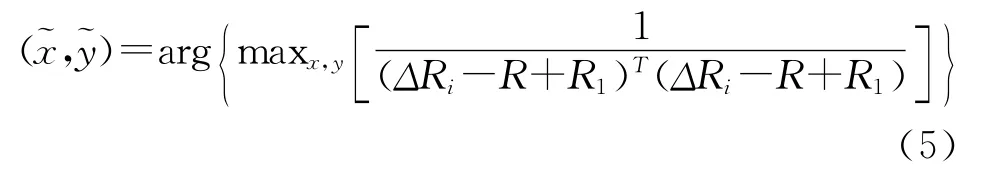
该方程式非线性函数，用解析法求解时比较困难。针对此情况，文中应用量子遗传算法来求解，采用似然函数的倒数作为个体适应度来选取优良个体，确定量子旋转门，用二进制数对个体进行编码，然后在确定的坐标范围内搜索移动台的位置。

3 量子遗传算法［8～9，11］

量子遗传算法（quantum genetic algorithm，QGA）是量子计算理论和遗传算法原理相结合的产物。主要以量子理论和量子计算为基础，采用量子比特实现染色体编码，通过量子门对其进行更新，产生种群的多样性。QGA具有种群规模小、寻优能力强、收敛速度快和计算时间短的特点。

3.1 量子比特编码

在量子信息论中，信息的载体不再是经典的比特，而是量子比特或量子位。量子比特可以处于0和1这两个基态的任意叠加状态。一个量子计算比特可以表示为：

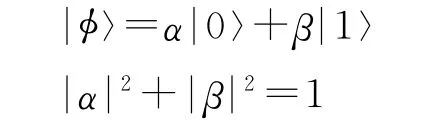
其中，α和β是两个复数，分别表示状态｜0〉和状态｜1〉的概率幅。｜α｜2和｜β｜2分别表示量子比特处于｜0〉和｜1〉的概率。

一个m位量子比特的编码形式如下：

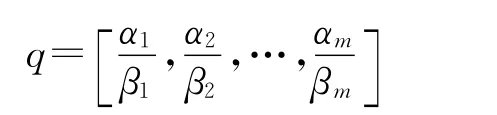
其中，｜α｜2＋｜β｜2＝1，一个m位量子比特编码可表示2m个不同的状态。

3.2 量子旋转门

量子旋转门是演化操作的执行机构，其调整操作如下式：

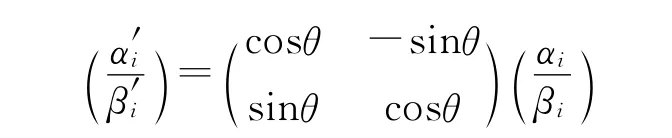
其中，（αi／βi）为种群个体第i个量子位，（α′i／β′i）为更新后的形式，θ为量子门的旋转角，θ＝Δθ·s（αi，βi），Δθ调整的步长值影响收敛速度，如果太大，算法易出现早熟现象而陷入局部最优解；如果太小，可能出现停滞状态，因此，需要自适应调整搜索。本文Δθ取10e－t／maxt，t为进化代数，maxt为最大进化代数，s（αi，βi）是搜索方向函数，主要使算法向最优解的方向进行搜索，s（αi，βi）的取值如表1所示。

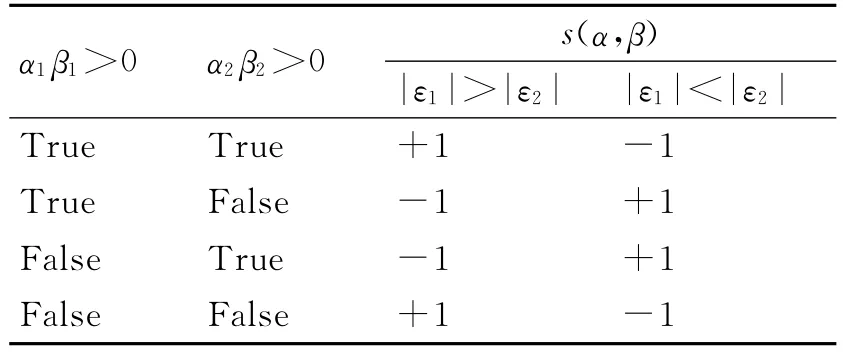
表1 函数s（α，β）的查询表

4 基于Chan-QGA的TDOA定位技术

用于定位的量子遗传算法流程简述如下：

1）根据Chan算法搜索到一个局部最优解（xa，ya），蜂窝的半径为r，确定量子遗传算法的搜索区间为［xa－C，xa＋C］和［ya－C，ya＋C］。在文中C＝r／4，若搜索区间超过蜂窝半径区间［0，r］，需做钳位处理。

2）根据给定的定位精度要求进行二进制编码产生初始种群，Chan算法搜索到的一个局部最优解（xa，ya）作为算法初始种群的一个个体，其他个体随机产生。

3）把似然函数的倒数作为当代种群适应度来计算，对种群的适应度进行评价，找出最优的个体保存起来。

4）用量子旋转门对种群进行更新。

5）判断算法迭代终止条件是否满足，如果满足，执行6）；否则，转向3）。

6）输出最优个体，Chan-QGA算法运行结束。

5 实验仿真及结果比较

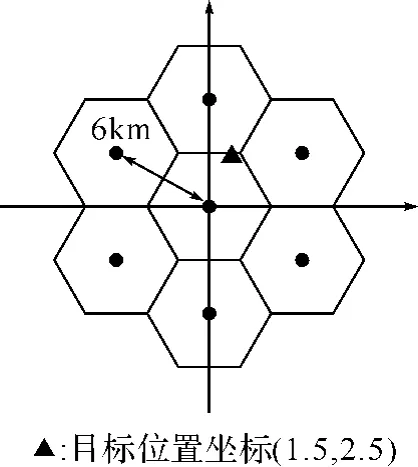
图2 接收机与目标位置示意图

表2中的Chan栏是Chan算法［1］的仿真结果；GA栏是文献［2］中改进算法的仿真结果；第一栏10lg（cσ）是根据蜂窝网通信系统与系统热噪声等因素确定的，评价指标为平均估计坐标MV，即E［（x，y）］；均方误差MSE＝E［（x－x0）2＋（y－y0）2］，仿真所得MV如表2所示，MSE如图3所示

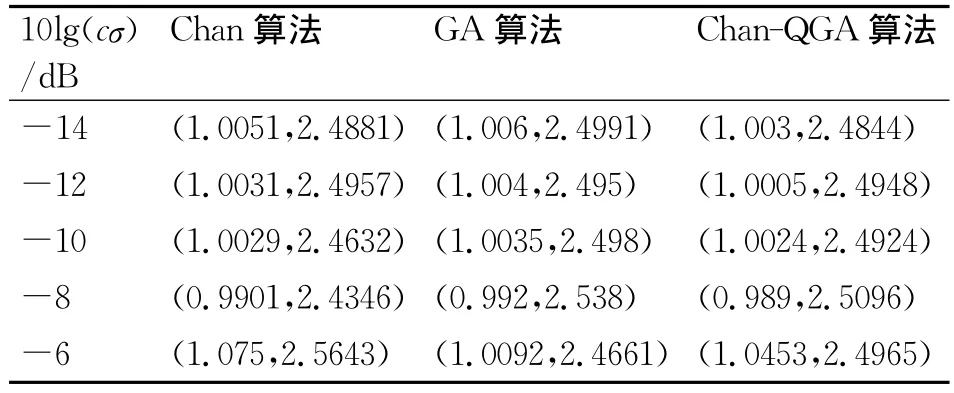
表2 Chan算法、GA算法及Chan-QGA算法

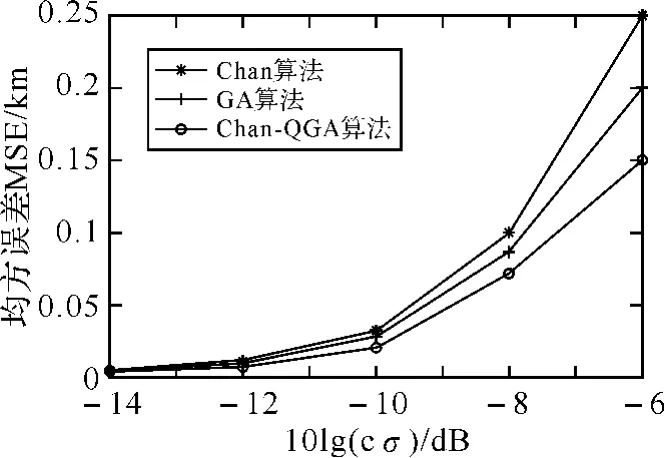
图3 Chan、GA、Chan-QGA的性能比较曲线

从图中可以看出，在噪声方差很小时，Chan-QGA与Chan、GA性能相近，但GA算法容易陷入局部收敛，而当噪声方差大时，GA、Chan-QGA的性能比Chan好，主要原因是Chan算法对噪声二次项的忽略导致的。另外还可以看出Chan-QGA算法性能好于GA算法，因为Chan-QGA算法引入了Chan算法的最优解，加快收敛速度。

6 结语

本文提出的Chan-QGA算法在仿真中表现稳定，定位精度高，特别在噪声较大的情况下，与Chan、GA算法相比，具有更高的稳定性、搜索速度和定位精度，对一些高精度的定位技术的研究有一定的应用价值。

［1］CHAN Y T，HO K C.A simple and efficient estimator for hyperbolic location［J］.IEEE Trans on Singal Processing，1994，42（8）：1905～1915

［2］李丽春，冉崇森，魏峰.利用改进遗传算法解决TDOA定位估计中的非线性优化问题［J］.系统工程与电子技术，2003，25（8）：971～973

［3］范平志，邓平，刘林.蜂窝网无线定位［M］.北京：电子工业出版社，2002

［4］FANG B T.Simple solutions for hyperbolic and related position fixes［J］.IEEE Trans Aerosp Eletron Syst，1990，26：748～753

［5］SMITH J O，ABEL J S.Closed-form least-spuarens source location estimation from range2difference measurements［J］.IEEE Trans Acoust Speech，Singnal Processing，1987：ASSP-35：1661～1669

［6］丛琳，沙宇恒，焦李成.基于免疫克隆选择算法的图像分割［J］.电子与信息学报，2006，28（7）：1169～1173

［7］孙胜，李辉，韩崇昭，等.基于TDOA定位技术的仿真研究［J］.无线通信技术，2002，11（4）

［8］吴涛，叶晓慧，王红霞，等.基于量子遗传算法测试选择问题的研究［J］.计算机测量与控制，2010，18（11）

［9］赵知劲，彭振，郑仕链，等.基于量子遗传算法的认知无线电频谱分配［J］.物理学报，2009（2）：1358～1359

［10］刘信新，陈鲲.基于RSSI与TDOA的混合测距加权定位算法［J］.计算机与数字工程，2011，39（4）

［11］罗红明，王家映，朱培民，等.量子遗传算法在大地电磁反演中的应用［J］.地球物理学报，2009（1）：261～263