算术编码理论及误差分析研究＊

韦 伟 游 彬 万 福 刘俊起

（海军指挥学院信息战研究系 南京 211800）

1 引言

在数字时代飞速发展的今天，压缩技术已经成为数据传输中必不可少的关键技术，数据压缩就是在一定精度所要求的条件下，以最少的数码表示信息所发出的信号。数据压缩技术分为：无损压缩和有损压缩。无损压缩是指将压缩后的数据进行还原，还原后的数据与原来的数据完全相同。有损压缩是指压缩后的数据还原后与原来的数据有所不同，但不会造成人对原始资料表达的信息造成误解。

早在1948年C.E.Shannon［1］提出信息论的时候，就提出了算术编码的思想。算术编码的概念是Elias在上世纪六十年代初期提出来的，直到八十年代才开始进入实用化阶段。Langdon［2］和Rissanen［3］等人在此期间对算术编码作了大量的理论研究。算术编码属信源编码［4］，信源编码又分为离散编码和连续编码，算术编码也属于离散编码。论文主要通过对算术编码和译码的分析从而得出算术编码在实际应用中出现的误差，本文最后还阐述了在程序算法设计中通过损失精度来实现算术编码的思想。

2 算术编码理论的基本思想

算术编码的基本思想是：从整个符号序列出发，将各信源序列概率映射到［0，1）区间上，使每个符号序列对应于区间内的一点，也就是一个二进制的小数。这些点把［0，1）区间分成许多小段，每段的长度等于某一信源序列的概率。再在段内取一个二进制小数，其长度可与该序列的概率匹配，达到高效率编码的目的［5］。这种方法与香农编码法比较类似，只是两者考虑的信源对象有所不同，在香农编码中研究的是单个信源符号，而在算术编码中研究的是信源符号序列。

定义各符号的积累概率为：

则由式（1）可得：P1＝0；P2＝p1；…；Pn＝Pn－1＋pn－1。如图1所示累积概率的分布。

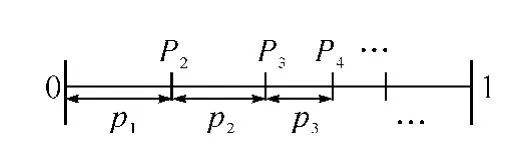
图1 信源符号对应的概率区间

对于整个信源符号序列而言，要把一个算术码字赋给它，就必须确定这个算术码字所对应的位于［0，1）区间内的实数范围，即由整个信源符号序列的概率本身确定0和1之间的一个实数区间。随着符号序列中的符号数量的增加，用来代表它的区间减小，而用来表达区间所需的信息单位（如比特）的数量则增大。

每个符号序列中随着符号数量的增加，即信源符号的不断输入，用于代表符号序列概率的区间将随之减小，区间减小的过程如图2所示。

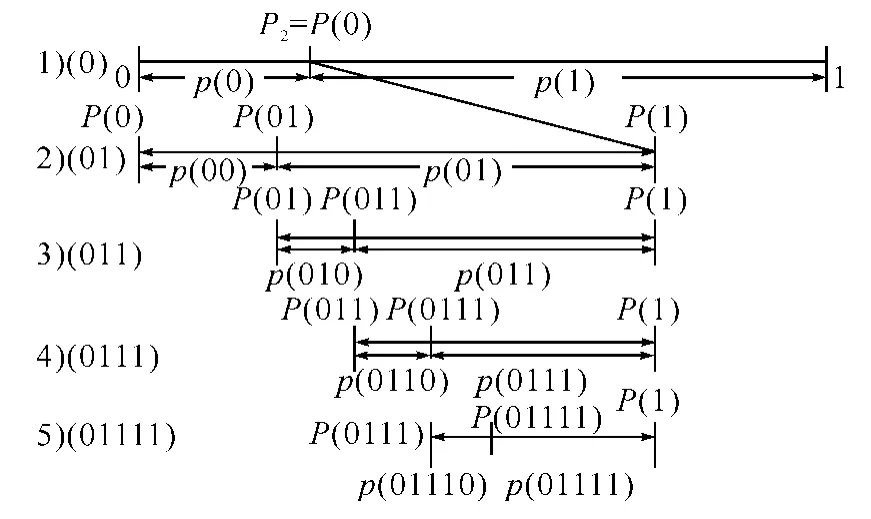
图2 以二元序列为例

由图2我们可以发现，输入信源序列为｛01111｝，当输入第一个‘0’时，概率空间被分割成两部分，p（0）和p（1）两个部分，代表‘0’的是p（0）区间；再输入‘1’时，p（0）区间再次分割，分割成p（00）和p（01）两个区间，其中p（01）区间表示‘01’输入；以此类推，可以得到代表‘01111’的区间是p（01111）。

我们在输入序列对应的区间内任意取一点，代表输入序列，并将取得的这个点作为依据进行编码，这种方式所得到的码字就称为算术编码。

3 算术编码的译码理论

算术编码译码的过程其实就是编码过程的逆过程，先根据编码所得码字确定第一个码字所在的范围，再将原本的［0，1）继续按信源分布概率减小，继续将累积概率和划分的区间进行比对，从而得出第二个码字，以此类推，从而不断得出原来的码字。

以二进制编码为例，每一步比较C－P（α）与A（α）p（0），这里α为前面已译出的序列串，A（α）是序列串α对应的宽度，P（α）是序列α的累积概率值，即为α对应区间的下界值，A（α）p（0）是此区间内下一个输入为‘0’所占的子区间宽度。

译码规定为：

若C－P（α）＜A（α）p（0），则译输出符号为0；

若C－P（α）＞A（α）p（0），则译输出符号为1。

由此，我们引入一个例子［5］，设二元无记忆信源S＝｛0，1｝，其中p（0）＝0.25，p（1）＝0.75。对二元序列α＝11111100进行算术编码，编码后并进行译码验证。我们可以得到α序列发生的概率为p（α）＝p（111111100）＝ （0.75）6（0.25）2＝0.01112366。

我们通过一种算术编码方式确定α的算术码字长度，L可以等于p（α）的倒数的对数，其值为6.49，6.49 ＝7；可以得出P（α）的累积概率为0.82202148。

信源符号序列α的累积概率值的变化和区间宽度减小的过程如图3所示。累积概率p（α）为输入符号序列11111100的下界值。

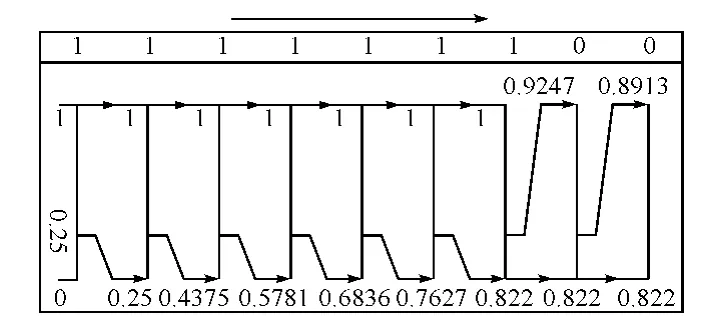
图3 算术编码过程区间宽度减小图解

取p（α）二进制表示小数点后L位，得到信源符号序列α的算术码字为‘1101010’。则平均码长为¯L＝0.875，编码效率为：η＝0.927。

4 算术编码译码误差分析

通过上面的分析，我们可以很容易地看出，在信源符号的不断增加中，长符号序列和短符号序列相比，误差在不断增加。而整个［0，1）区间在不断减小，随着概率区间的减小，累积概率对概率的精度要求越来越高，从而算术编码的误差就在不断增加。

以上面的例子来看，最后所得的码为1101010，化成十进制码后为0.828125，与原来的累积概率0.82202148相比较，千分位数据相差太大。我们在译码的时候可以发现，0.828125首先处在［0，1）的后3／4中，则译出第一位码为1，之后考虑［0.25，1）区间，0.828125又处在后3／4处，第二位再译出一个1，以此类推，具体过程如图4所示。

最终导致我们译码的时候小数点后第七位和第八位无法准确译出。所以算术编码具体编码方式的选择还存在一定的问题。

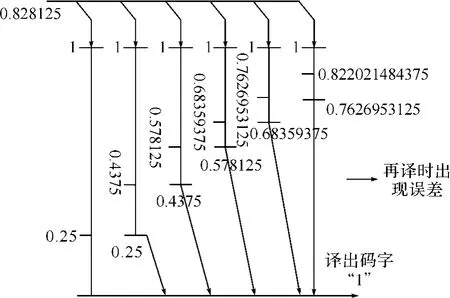
图4 译码误差分析

对于上述问题的解决方式目前只能通过在放弃一定精度的情况下编码，Ian H.witten、Radford M.Nea和John G.Cleary等人发表论文［6］，提出了一种基于整数运算的算术编码实现算法。在算法实现中，通过改进算法，把映射的区间扩大，如使用［0，1000）这个区间来映射概率。这样，在处理过程中，精度比用［0，1）区间损失更大，但其优点是处理速度加快，编码容易。在编码的过程中，还通过正规化提取等操作使得算法速度更快，效率更高［7］。

5 结语

本文分析了算术编码的编码和解码理论，具体指出了编码方式中的一些误差和缺陷。通过本文，读者可以对算术编码有更为清晰的认识，对算术编码的编码选择方式，译码过程会有更深的体会。算术编码本身具有很好的数据屏蔽性能［8～9］，可以同时实现压缩加密，而仅需损失少量的编码效率。目前，算术编码在图像压缩标准（如JPEG）［11］中得到了广泛的应用，希望本文对算术编码的具体实用人员有所帮助。

［1］C.E.Shannon.A mathematical Theory of Communication［J］.Bell System Technical Journal，1948，27：379～423，623～656

［2］Langdon G G，Jorma Rissanen.Compression of Black-White Images with Arithmetic Coding［J］.IEEE Trans.Commun.COM-29，1981（6）：858～867

［3］Langdon G G，Jorma Rissanen.A Double Adaptive File Compression Algorithm［J］.IEEE Trans.Commun.COM-31，1983：1253～1255

［4］John G.Proakis.Digital Communications（Fourth Edition）（张力军，张宗橙，郑宝玉，等译）

［5］冯桂，林其伟，陈东华.信息论与编码技术［M］.北京：清华大学出版社，2007，3

［6］Ian H.witten，Radford M.Nea，John G.Cleary.A-rithmetic Coding for Data Compression［J］.Communications of the ACM，1987，30（6）：520～541

［7］编 程 论 坛 ［EB／OL］.http：／／programbbs.com／bbs／view12-29356-1.htm

［8］倪兴芳，姜峰.算术编码与数据加密［J］.通信学报，1999，20（4）

［9］彭云，任俊彦，叶凡，等.一种适于硬件实现的算术编码算法［J］.通信学报，2001，22（2）

［10］倪桂强，李彬，罗健欣.BWT与经典压缩算法研究［J］.计算机与数字工程，2010，38（11）

［11］余成波.信息论与编码基础.北京：机械工业出版社，2005