人／椅系统外流场的数值模拟＊

丁春全 姜 南 范 群

（襄樊市157信箱1） 襄樊 441003）（中航工业航宇救生装备有限公司2） 襄樊 441003）

1 引言

飞行员应急弹射时，人／椅系统出舱后就暴露在空气流场中。气动载荷对系统的稳定性影响极大，同时高速气流还会对飞行员造成伤害。因此分析人／椅系统的气动特性对弹射救生系统的性能设计非常重要。本文采用数值模拟方法对典型钝头体模型二维半圆柱外绕流进行数值模拟，并将数值模拟结果与实验值进行对比、修正；然后将此计算方法应用于人／椅救生系统外流场的计算。

2 二维半圆柱外绕流的数值模拟

二维半圆柱外绕流的计算条件为［1］：马赫数Mα＝0.177，雷诺数Re＝8.27×106。计算时首先应用第二章介绍的Hilgenstock法网格生成法生成计算网格。为了检验第一内节点到边界的距离对壁面函数的影响，本文共生成了三套不同距离的计算网格，生成的网格具体如图1和2所示。

图1 全部计算网格

图2 计算网格局部

2.1 数值模拟方法［2～4］

用控制容积法对曲线坐标下的控制方程进行离散，控制方程中对流项的离散格式采用MUSCL格式，速度与压力修正采用同位网格下的SIMPLER算法，湍流模型采用标准k－ε两方程模型，近壁区采用两层壁面函数JL法处理，离散后的代数方程组采用SIP算法进行求解。

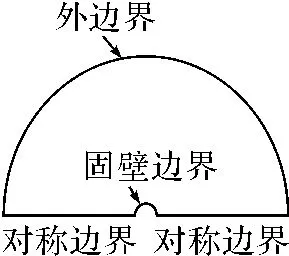
图3 算例计算域的示意图

2.2 边界条件

本算例的计算域如图3所示，取圆柱的一半进行计算，为了减小边界对计算的影响，计算域的外径为计算圆柱的50倍。计算中采用的边界条件如下：

外边界条件：u＝U∞为自由来流；v＝0；压力采用二阶外推；湍流动能和耗散率按下式计算：

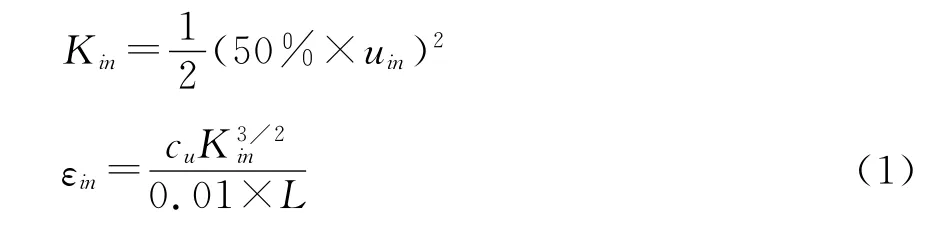
上式中：L为特征长度，取圆柱的直径。

对称面处边界条件：v＝0；其它参数符合dφ／dy＝0。

2.3 计算结果

图4、图5和图6分别为圆柱外速度矢量、流线和压力分布图。从图中可以看出，流体流过圆柱后产生分离，并在圆柱后形成了涡区。

图4 圆柱后速度矢量图

图5 圆柱外绕流流线图

图6 圆柱外压力分布图

图7 三种第一节点到壁面距离，一阶迎风格式（Upwind）下，压力系数在圆柱外壁上的周向分布图

图7为三种第一内节点到壁面距离条件下，对流项采用一阶迎风格式时，压力系数Cp在圆柱外壁上的周向分布图。从图中可知随着第一内节点到壁面之间距离的减小，计算值与试验值的误差逐渐减小。

图8、图9和图10三图分别为对流项采用Upwind格式和MUSCL格式计算的CP在圆柱外壁上的周向分布图。图中均反映出高阶精度对流项离散格式的计算结果较低阶的计算结果好。由于两层壁面函数本身存在的固有局限性，使得在使用其进行计算时，需要调整第一内节点到壁面的距离，从图中可以看出采用第一种距离所得计算结果与试验结果更接近。通过对该算例的计算可以看出，采用本文的数值模拟方法和编制的计算程序可以对大钝头体外的流动进行数值模拟，并且计算结果的精度较好（其中试验数据来源参考文献AIAA-94-0751）。

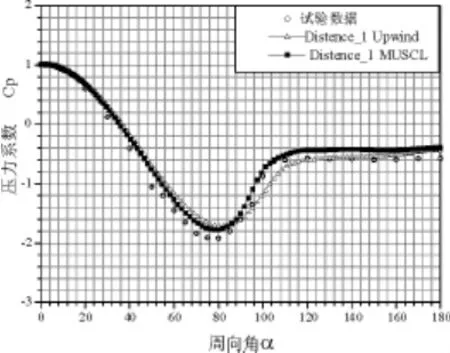
图8 第一种距离，Upwind格式和MUSCL格式计算的压力系数在圆柱外壁上的周向分布图

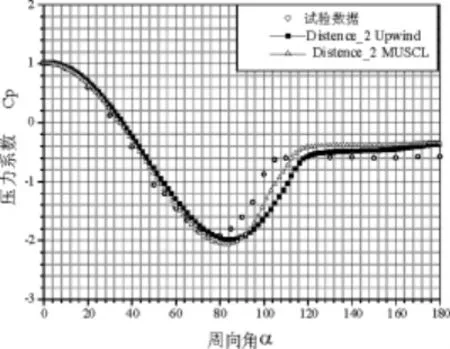
图9 第二种距离，Upwind格式和MUSCL格式计算的压力系数在圆柱外壁上的周向分布图

3 人／椅系统外绕流的数值模拟

本文用数值模拟的方法来模拟自由飞阶段人／椅系统的外流场，没有考虑弹射过程中飞机、舱盖对人／椅系统的影响等，也没有对人／椅系统的运动进行模拟。因此，计算中也没有考虑座椅椅载火箭载荷和降落伞减速载荷的作用。

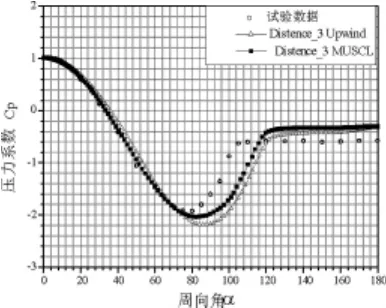
图10 第三种距离，Upwind格式和MUSCL格式计算的压力系数在圆柱外壁上的周向分布图

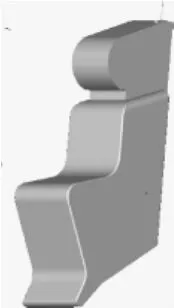
图11 简化的人／椅系统模型

3.1 人／椅系统几何模型的简化

人／椅系统的外形随着飞行员的个体差异以及个体防护装备的不同，个体的具体外形有较大差异。为了使本文计算结果具有一定的典型意义，本文对人／椅系统的外形进行了简化。以某型座椅的尺寸为参考，根据GJB规定的第百分之五十分位的飞行员人体尺寸，考虑到头部、躯干、下肢的尺寸，经过简化，设计出计算用人／椅系统的外形几何尺寸（如图11所示）。国外在计算人／椅系统的气动特性时，也采用了类似的简化［5］。

3.2 计算对象

图12 二维人／椅系统的外形图

从图11可知该模型为几何对称模型，本文仅对中心对称面形成的封闭二维外形的气动特性进行了数值模拟。图12为本文的计算固壁外形，为保证自由来流的边界条件，计算域取得足够大。根据第二章介绍的网格生成方法可以生成计算用网格。为了比较Thomas和Middlecoff法和Hilgenstock法在本计算中的网格生成情况，分别采用两种方法生成了计算网格，从图13（a）、13（b）中可看出 Thomas和Middlecoff法和Hilgenstock法生成网了计算网格，从图13（a）、13（b）中可看出Thomas和 Middlecoff法和Hilgenstock法生成网格的区别。很明显Hilgenstock法对边界处网格的正交性和计算网格的第一内点到边界的间距可以直接加以控制，网格质量好。所以用Hilgenstock法生成的网格作为计算用网格。

3.3 数值计算方法

计算中，湍流模型采用标准－两方程模型，将所有方程从笛卡尔坐标系转换到贴体坐标系下，然后用控制容积法对曲线坐标下控制方程进行离散。控制方程中对流项的离散格式采用了MUSCL格式，速度与压力修正采用同位网格下的SIMPLER算法，湍流近壁区采用两层壁面函数JL法处理，离散后的代数方程组采用SIP算法进行求解。

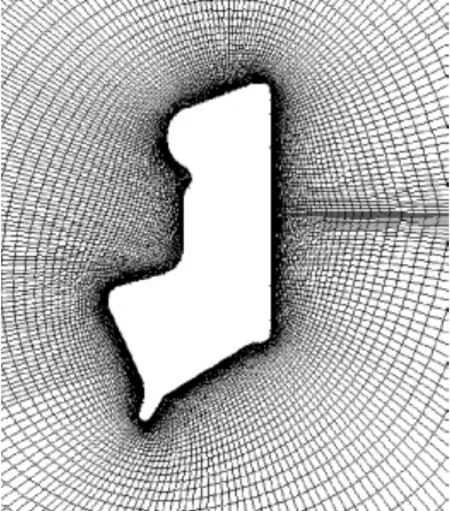
图13（a） Thomas和Middlecoff法

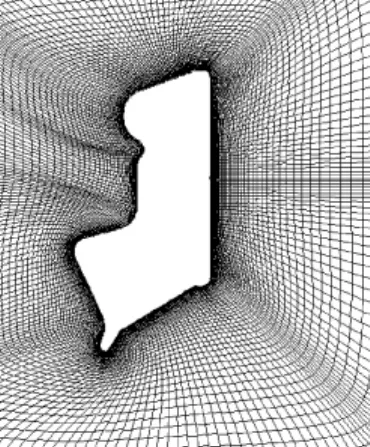
图13（b） Hilgenstock法

3.4 边界条件

自由来流边界：u＝U∞、v＝0，紊流动能的取值为：k＝（0.0005×U∞2），紊流耗散的取值为：ε＝cμk2／3／l、l＝lmcμ1／4，压力采用二阶外插得到。固体壁面：各固体壁面采用非滑移条件—速度均为零，紊流动能和紊流耗散率在固壁面上采用两层壁面函数JL法处理，压力采用法向一阶导数为零。

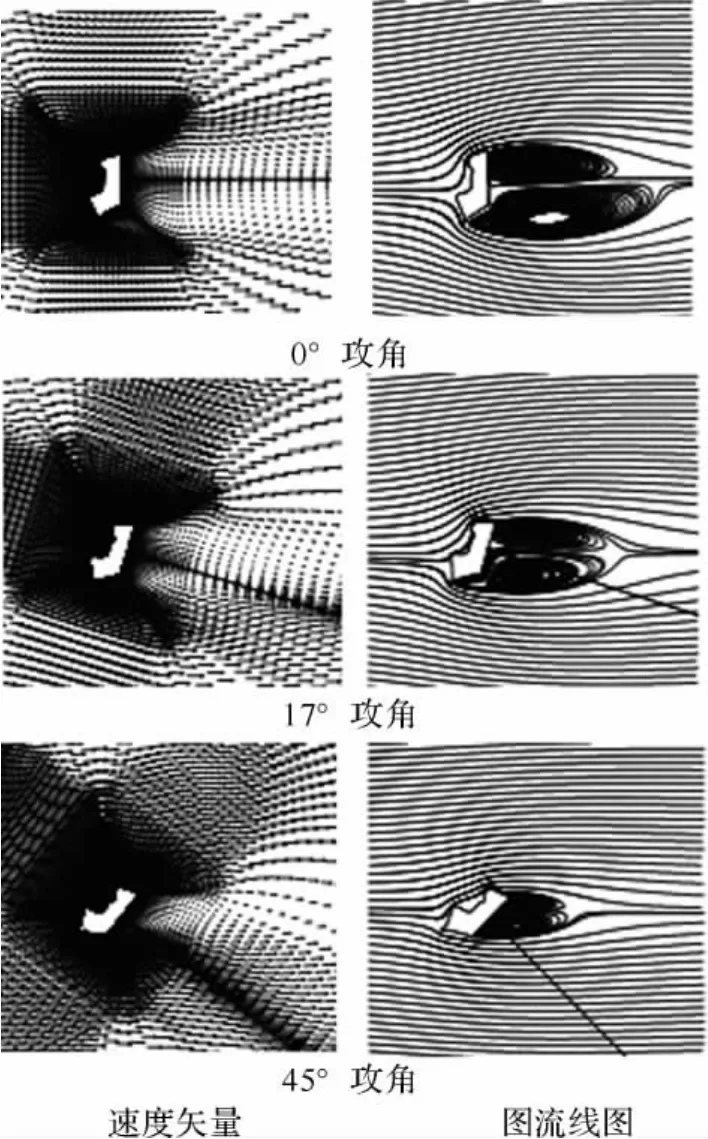
图14 人／椅系统外流场

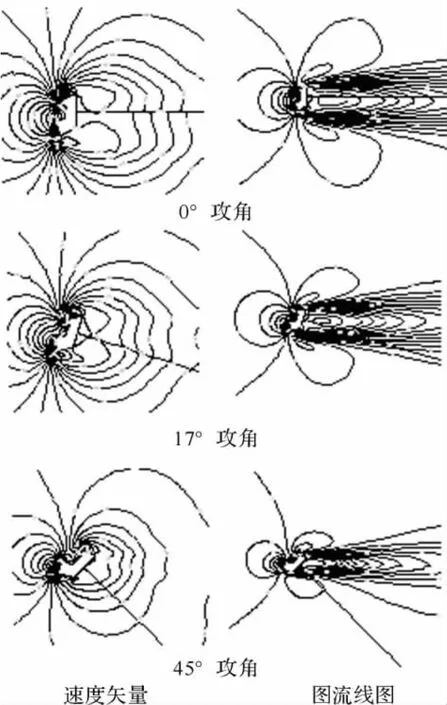
图15 人／椅系统压力分布及速度分布图

对称面处边界条件：v＝0；其它参数符合dφ／dy＝0。

3.5 计算结果及分析

本文所模拟的人／椅系统外空气的流动参数为：Mα＝0.177，雷诺数为Re＝4.28×106，此参数取自某型座椅的风洞试验工况。具体计算结果如图14、15所示。

图14、15中可以看出人／椅系统是一个典型的大钝头体，其后部存在较大的分离区，头部和脚尖分别有流动加速区。随攻角的增大人／椅系统后部的分离区越来越小，也即人／椅系统对下游的流动影响减小；同时头部和脚尖的负压区和负压值也越来越小。（在计算的0°－45°攻角范围内，共计算了20组数据，本文列举三组数据情况用于分析）。

4 计算结果对工程设计的意义

从计算结果的压力分布图可以明显地看出对称平面的压力情况：正面压力为正，上部、下部和后部为负压区。其中脚背部、小腿、胸腹部，下颌及脸的下部的压力较大，头顶部和脚的后部压力较低。这表明头部会有升力，胸腹部有较大的压力作用，这些作用力超过一定范围时会对飞行员造成伤害，因此在设计上应有所考虑降低这些作用（特别是在高速时）。由人／椅系统的压力、速度分布可知在人／椅系统的前部加一分流装置，可以改变其正前方的压力，也可以减小头部的升力。

从计算结果可知座椅的后部是一个较大的负压力湍流区，对于给人／椅系统起稳定作用的稳定伞应尽量避免在该区域工作，本计算结果可以为工程设计时伞椅连接装置（如伞绳或稳定杆）的长度及安装位置提供依据。

［1］G.S.Hufford，S.D.Habchi.Validation of CFD Methodology for Ejection Seat Applications.1994，AIAA-94-0751

［2］Simon Gant.Development and Application of A New Wall Function for Complex Turbulent Flows.PHD thesis，Insititute of Science and Technology，University of Manchester，2002

［3］C.C.Chieng，B.E.Launder.On the Calculation of Turbulent Heat Transport Downstream from an Abrupt Pipe Expansion，Numer.Heat Transfer.Prog.Heat Mass Transfer，1980，3：189～207

［4］R.W.Johnson，B.E.Launder.Discussion of“On the Calculation of Turbulent Heat Transport Downstream from an Abrupt Pipe Expansion”.Numer.Heat Transfer，1982，5：493，496

［5］D.C.Kenzakowski，B.J.York，S.M.Dash.Computational Simulation of Ejection.Seat Aero dynamics With Rocket Propulsive Effects.1997，AIAA-97-2253