基于STFT的跳频信号参数估计＊

卢云生 董英英

（中国电子科技集团公司第三十六研究所1） 嘉兴 314033）（武汉软件工程职业技术学院2） 武汉 430250）

1 引言

频率跳变系统是频率跳变扩展频谱通信系统的简称，它是用二进制伪随机码序列去控制射频载波振荡器输出信号的频率，使发射信号的载波频率随伪随机码的变化而跳变［1］。频率跳变系统可供随机选取的载波频率数通常是几千到几万个离散频率，在如此多的离散频率中，每次输出哪一个由伪随机码决定。

跳频信号的基本特征参数有：跳频速率。跳频信号在单位时间内的跳频次数；驻留时间。跳频信号在一个频点停留的时间，其倒数是跳频速率，它和跳频图案直接决定了跳频系统的很多技术特征；频率集。跳频电台所使用的很多频率的集合构成跳频通信网台的频率集，其完整的跳频顺序构成跳频图案；跳频范围。又称为跳频带宽，表明跳频电台的工作频率范围；跳频间隔。跳频电台工作频率之间的最小间隔，或称为频道间隔，通常其他的频率差是跳频间隔的整数倍。上述参数中的跳频范围、跳频间隔、跳频图案、跳频速率是跳频通信网台的“指纹”参数，是通信侦察系统进行信号分选的基础。

2 跳频信号的短时频域分析

跳频信号由于其频率是时变的，故而它是一种非平稳的信号。考虑到跳频信号的非平稳性，本文采用短时傅里叶变换（STFT）对其进行分析。

短时傅里叶变换（STFT）是一种时频分析工具，它表示信号的时间－频率能量分布，它是对时域信号加窗之后的傅里叶变换［2～3］。设窗函数为w（n），信号为x（n），则x（n）的STFT的表达式如下：

可以发现，当窗宽小于等于一个码元宽度时，窗内存在两种情况：单一频率和两种频率［4～6］。幅频图表征的是信号能量在各个频段的分布，可以认为一个窗内的信号能量是相同的，那么当只存在一个频率时，其能量将集中在该频率，如图1所示；当有两个频率时，信号能量将会被分到两个频点，这样导致频谱峰值下降，如图2所示；当两个频率在时域上时长相同时，能量被等分，此时频谱峰值最小，如图3所示。此时窗的中心即为频率跳变时刻，峰值对应的频率即为信号的频率。

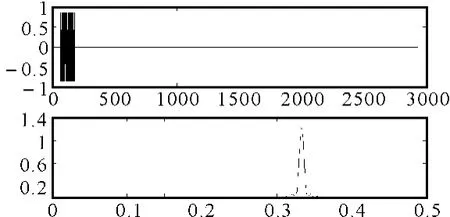
图1 单一频率时的频谱图

图2 同时存在两个频率时的频谱图

图3 两个频率时长相等时的频谱图

3 跳频信号参数估计

3.1 跳频周期估计

由第2节对跳频信号的短时频域分析可知，当窗函数移动到频率跳变时刻时频谱峰值最小，频谱峰值近似周期性变化。因此，可以通过计算STFT（t，f）在各个时刻t的最大值，得到y（t），用傅里叶变换估计y（t）的周期，得到跳频周期的估计值Th1。计算出信号在各个时刻STFT的最大值y（t）如图4所示。

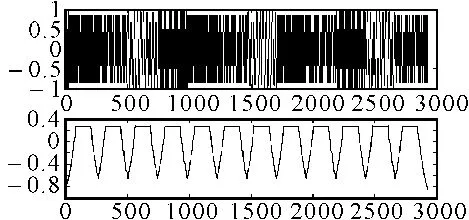
图4 信号在各个时刻STFT的最大值y（t）

图5 跳频信号时频图

由图4可以看出，y（t）的波形并非正弦或余弦信号，而是包含较多频率分量，所以用FFT对y（t）进行频率估计后的结果与真实的跳频频率有误差，需要通过跳频时刻的测量来对跳频周期进行修正。这里计算出的跳频周期Th1仅作为y（t）谷值位置计算的一个参考。

3.2 跳频时刻估计

由图4可以看出，y（t）的谷值对应的就是信号的跳频时刻，但由于参数估计是在未知任何先验信息的情况下进行的，接收的信号第一个和最后一个码元可能不完整。y（t）的谷值时刻对应的是信号频率跳变的时刻，但频率跳频时刻不一定会产生谷值，这通常发生在信号样本的起始和末尾处。因此，对于那些特殊的跳频时刻需要通过以下算法来求出：

1）用一个窗宽略小于Th1的矩形窗与y（t）相乘，矩形窗从左至右连续移动并计算其对应的最小值，如果最小值位于窗的中心，则此时的矩形窗中心为y（t）的谷值，也即信号跳频时刻。

2）根据第一步求出的跳频时刻，求平均时间间隔得到跳频周期Th。

3）如果求出的第一个跳频时刻y1＞Th，则y1－Th时刻为特殊跳频时刻，也即第一个完整码元的起点。同样的方法可以求出最后一个完整码元的终点。

3.3 跳频频率估计

计算出跳频时刻后，各个时刻之间的信号就为单一频率，分别对其求STFT，取频谱最大值，就可获得对应频率。计算出图4中跳频信号的时频图如图5所示。

4 窗宽对参数估计的影响

窗的宽度对于信号参数估计有很大影响，窗宽过大将会产生码间串扰，太小则取样数据太少将丢失信号信息。对图4中的跳频信号，分别仿真计算出窗宽等于码元宽度0.02倍、0.1倍、2倍和2.2倍时的频谱图，如图6～图9所示。

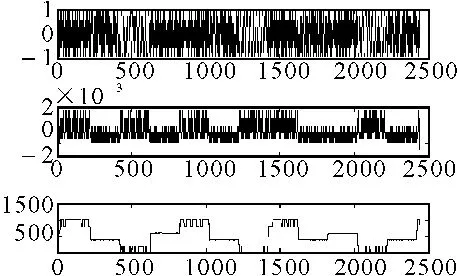
图6 窗宽等于码元宽度的0.02倍

图7 窗宽等于码元宽度的0.1倍

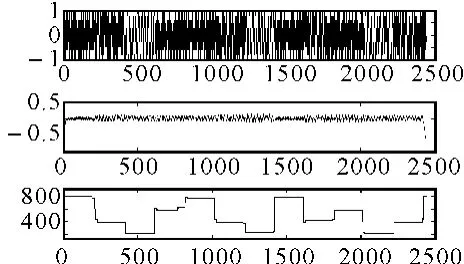
图8 窗宽等于码元宽度的2倍

图9 窗宽等于码元宽度的2.2倍

通过对比可以看出，窗宽对于跳频信号参数估计有很大影响，窗宽过大将会产生码间串扰，太小则取样数据太少将丢失信号信息。实际应用中取窗宽等于码元宽度的0.1倍即可达到较好的参数估计效果。

5 结语

针对跳频信号的非平稳性和频率的时变性，本文采用短时傅里叶变换（STFT）对跳频信号进行了分析，并基于STFT对跳频信号的跳频周期、跳频时刻和跳频频率等参数进行了估计。最后分析了窗宽对参数估计的影响。仿真结果表明，采用STFT方法可以有效估计出跳频信号的特征参数，为通信侦察系统进行信号分选打下良好的基础。

［1］梅文华.跳频通信［M］.北京：国防工业出版社，2005

［2］胡广书.现代信号处理教程［M］.北京：清华大学出版社，2004

［3］赵俊，张朝阳，赖利峰.一种基于时频分析的跳频信号参数盲估计方法［J］.电路与系统学报，2003，8（3）：46～50

［4］朱文贵，戴旭初，徐佩霞.一种跳频信号参数估计的方法［J］.小型微型计算机系统，2008，29（4）：761～764

［5］吴敏健，徐佩霞.基于遗传算法的跳频信号盲估计［J］.无线电工程，2005，35（10）：3～5

［6］郑文秀，赵国庆，罗勇江.跳频信号的跳速估计［J］.系统工程与电子技术，2006，28（10）：1500～1501

［7］张丹，吴瑛.STFT在跳频信号分析中应用［J］.现代电子技术，2006，28（10）：60～61

［8］张曦，杜兴民，朱礼亚.基于重排SPWVD的跳频信号参数提取方法［J］.计算机工程与应用，2007，43（15）：144～147

［9］熊俊俏.STFT算法在短波差分跳频信号检测中的应用［J］.电讯技术，2010，50（8）：52～55

［10］刘超，曾超，吴国安，等.一种跳频滤波器性能自动测试系统［J］.计算机与数字工程，2011，39（4）

［11］万果果，张元，李建武，等.一种对统计信号处理中缺失数据估计的算法［J］.计算机与数字工程，2010，38（10）

［12］FLANDRIN P，MARTIN W.Pseudo-wigner estimators for the analysis of nonstationary processes［C］／／Proc.IEEE Spectr.Est.WorkshopⅡ，Tampa，FL，1983，11：181～185