联合测高重力异常与ETOPO5海深数据求解南海海深模型

聂琳娟，吴云孙，金涛勇，超能芳

( 1.武汉大学 测绘学院，湖北 武汉 430079；2.湖北水利水电职业技术学院，湖北 武汉 430070)

高精度、高分辨率的海深模型对于物理海洋学、海洋生态学、海洋地质学等相关地球学科的研究十分重要.在深海区域，由于沉积与侵蚀作用速度缓慢，高精度、高分辨率的海深模型对于探测地幔对流模式，确定板块边界，研究海洋岩石圈的冷却和年龄以及洋脊底部火山的分布有着重要的作用.此外，当采用水文动力学方法研究和建立全球海洋潮汐模型时，高精度、高分辨率的海深模型也是必需的.传统的海深测量方法难以实现全球范围内的全面探测.利用基于卫星重力探测技术获取的海洋重力数据，通过重力反演，为构建全球海洋海底地形模型和探测研究海底构造提供了现实可能.

本文联合测高重力异常及ETOPO5海深数据求解南海海深模型，考虑到南海地区地质构造复杂，为更好地刻画南海海底地形地貌，综合采用了解析法和统计法，联合测高重力异常和ETOPO5海深模型，反演计算更精细的南海海底地形.

1 非补偿板块模型反演海深原理

在频域，重力异常和海底地形存在如下线性关系：

H(u,v)=Z(u,v)ΔG(u,v)

(1)

式中H和ΔG分别是海深和重力异常的傅立叶变换，Z为转换函数.事实上，海深和重力异常之间的关系是非线性的.但是，在许多大地测量计算中，非线性问题可以通过使用合适的参考场线性化.其主要原理是将信号或场(诸如重力异常)分解为长波部分和短波部分，长波部分即为参考场，短波部分为残差场.公式(1)所描述的线性关系更适合于残差场.基于上述原理，可以采用Watts非补偿板块模型来反演海深，公式为：

(2)

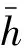
2 反演海深模型的建立

利用格网ETOPO5海深模型进行内插，联合本区域内船测海深值，加权平均后通过最小曲线拟合法得到新的2′2′格网海深模型，即为初始模型.定权方法如下：船测海深误差为25 m，而ETOPO5海深模型与船测海深差值的RMS为400 m，因此，船测海深和ETOPO5模型海深的权分别为和

利用船测海深数据和ETOPO5海深模型建立了初始模型之后，就可利用测高重力异常来反演海深模型.利用式(1)和式(2)，反演海深模型计算步骤如下：

1)采用波长为110 km的高斯低通滤波器对海深初始模型进行滤波，得到参考海深，初始模型减去参考海深，得到残差海深；对重力异常采用同样的方法，得到残差重力异常.

2)将残差重力异常进行向下延拓，得到分层向下延拓残余重力异常值.由于参考海深值最大不超过8 000 m，故采用200 m的层间间隔得到了200～8 000 m的分层残余重力异常，其中为了避免高频分量的抖动，截除了波长小于15 km的分量.

3)对任一格网点，其平均海深可通过步骤1)的参考海深内插得到.利用平均海深，该点的向下延拓残差重力异常可通过分层重力异常内插得到.

4)在所有格网点，步骤1)得到的残差海深与步骤3)得到的向下延拓残差重力异常之比值被用来估计海底物质和海水的密度差Δρ.

5)根据估计的密度差，利用式(1)～(2)计算残余海深.

6)残余海深加上步骤1)中的参考海深得到反演海深模型.

3 线性回归与数据融合

不可避免地，上述得到的反演模型其高频分量存在震荡，需进一步进行处理.事实上，即使南海海底复杂构造已知，Watts的三板块模型也难以符合和刻画，并且其中所需的板块厚度和弯曲刚度等参数也难以准确计算.基于上述的不确定性，在建立海深模型的过程中，引入随机相关理论，采用线性回归模型：

(3)

式中:h为海深，Δg为重力异常，μh和μΔg分别为海深和重力异常的数学期望，Chg为海深和重力异常的互协方差阵，Cgg为重力异常的自协方差阵.在这种方法中，海深和重力异常被认为是两个随机变量，通过各自方差函数和数学期望来刻画.回归模型将产生估计量的最小误差方差.海深和重力异常的数学期望可以通过低通滤波得到：

μh=E(h)=Fλ(h)

(4)

μΔg=E(Δg)=Fλ(Δg)

(5)

式中:E为数学期望算子，Fλ为波长λ的低通滤波器.海深和重力异常的模型参考值即为各自的数学期望.式(3)还可表示为：

(6)

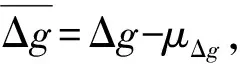
(7)

式中:F为傅立叶变换，Shg和Sgg为功率谱密度(PSD)函数，可以通过下式计算得到：

(8)

(9)

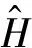
(10)

(11)

这里，u=qcosα，v=qsinα.通过等方性谱密度函数，式(7)可表示为：

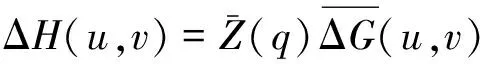
(12)

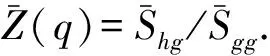
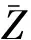
(13)

其中：σhg为海深和重力异常的协方差，σg为1°×1°区域内重力异常方差.

检验随着各种数据(包括船测深数据、卫星测高数据)的日益丰富，海深改正模型将不断得到更新，精度和分辨率也将不断得到提高.更新过程可用卡尔曼滤波来解释：

(14)

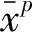
在实际应用中，加权平均法具有更大的优越性.因为该方法可以兼容质量较差的数据，具体做法是只要赋予质量较差的数据相对较小的权.对于利用卫星测高数据反演海底地形来说，由于近海卫星测高数据质量较差，因而近海反演的重力异常精度也较差.此外，由于海洋沉积物的存在，很难获取精确的转换函数.

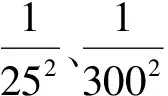
表1 海深反演模型、ETOPO5海深模型与LDEO船测海深比较结果

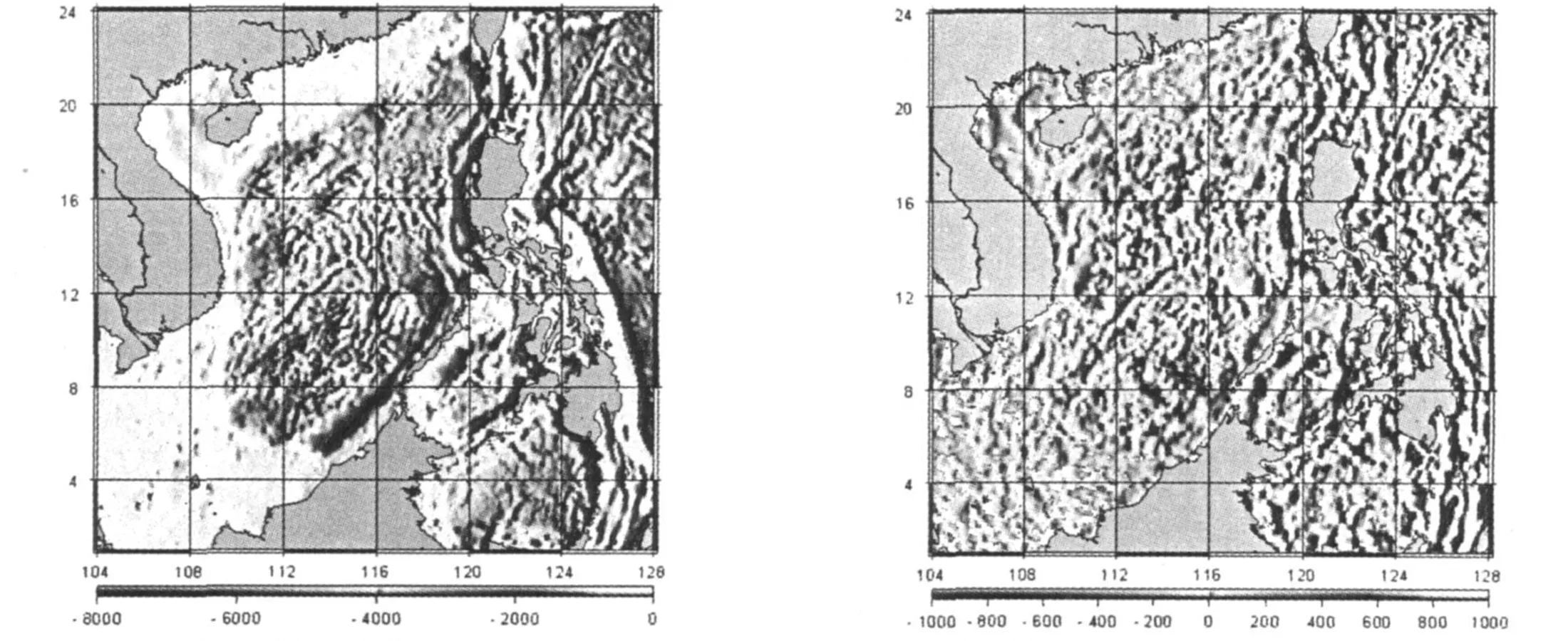
图1 反演海深模型(单位：m) 图2 反演海深模型与ETOPO5差值分布图(单位：m)

4 结论

本文利用已得到的联合测高重力异常及ETOPO5海深数据，采用Watts提出的非补偿板块模型，反演了南海海域海底地形模型.考虑到该方法为向下延拓问题，容易导致高频分量剧烈震荡，本文引入统计学中的统计相关理论，采用线性回归模型，对应用该方法得到的海深模型进行了处理，反演结果与LDEO船测深数据相比较，两者之差的RMS为253.3m，较ETOPO5海深模型精度和分辨率均有明显的提高.

参考文献:

[1]罗佳,李建成,姜卫平.利用卫星资料研究中国南海海底地形[J].武汉大学学报:信息科学版,2002,27(3):256-260.

[2]黄谟涛,翟国君,欧阳永忠,等.利用卫星测高资料反演海底地形研究[J]. 武汉大学学报：信息科学版,2002,27(2):133-137.

[3]Forsberg R，Tscherning C C．The use of height data in gravity field approximation by collocation[J]．J Geophys Res,1981,86(B9):7843-7854.

[4]Hwang C. Analysis of some systematic errors affecting altimeter-derived geoid gradient with applications to geoid determination overTaiwan[J]．Journal of Geodesy,1997,71:113-130.

[5]Hwang C. Inverse Vening Meinesz formula and deflection-geoid formula: applications to the prediction of gravity and geoid over theSouth China Sea[J].Journal of Geodesy, 1998,71:304-312.

[6]Jordan S K. Self-consistent statistical models for the gravity anomaly, vertical deflections and undulation of the geoid[J]．J Geophys Res,1972,77:3660-3670.

[7]Majumdar T J ,Bhattacharyya R. Bathymetry prediction model from high-resolution satellite gravity as applied over a part of the Eastern Indian Offshore[J].Current Science,2000，89:1754-1758.

[8]Wessel P.Thermal stress and the bimodal distribution of elastic thickness estimates of the ocean lithosphere[J].J Geophys Res,1992,97:14177-14193.