传递对准数字仿真系统Kalman滤波池设计

解春明，赵剡，王纪南，3

(1.北京航空航天大学仪器科学与光电工程学院，北京100191;2.桂林空军学院，广西 桂林541003;3.中国空导弹研究院，河南洛阳471009)

传递对准是用于解决捷联惯导系统空中动基座条件下初始对准问题的一项关键技术.特别是由于战术武器在现代局部战争中的作用日益突出，对捷联惯导系统对准的快速性和准确性提出了更高的要求［1］.

国内外对此问题的大量研究集中在对准匹配方案、滤波器的设计上.传递对准可采用的对准匹配方案很多，其中典型方案包括速度匹配、姿态匹配、速度+姿态匹配、位置匹配、速度+位置匹配、角速率匹配、速度+角速率、比力匹配等等，而且即使是同一种匹配方案，其状态方程和量测方程也不尽相同［2-12］.另外，对准所采用滤波器的配置参数及算法也很多［13-15］.因此，对准匹配及滤波的研究内容十分繁杂.

现有研究往往仅对特定的传递对准匹配方案、状态方程、量测方程、滤波参数以及滤波算法考虑，进而编制对应的程序.值得注意的是，当匹配方案、状态方程、量测方程、滤波参数以及滤波算法的任何部分发生变化时，都需首先做代码级修改，包括增删变量、修改赋值、模型修改、算法修改、输入输出修改等，然后再进行调试、发行，既浪费了开发时间，又不利于系统集成.

本文旨在为传递对准数字仿真系统设计通用的滤波机制，使仿真系统能够灵活方便地进行任意匹配方案、状态方程、量测方程、滤波参数、滤波算法的研究.由于传递对准通常采用Kalman滤波，因此本文设计的通用滤波机制称为Kalman滤波池.Kalman滤波池基于VC++6.0开发环境，结合数据库技术、动态链接库技术实现.用户可以摆脱代码编写的束缚，直接通过滤波池操作面板，进行传递对准匹配方案、滤波参数、矩阵等信息的填写、保存，使得现有文献提出的某种对准匹配模型压缩为滤波池的一条记录.滤波池根据用户需求提取记录信息，启动滤波过程，解析数据，调用导航、滤波算法，输出滤波结果.

1 传递对准Kalman滤波池设计

传递对准线性离散方程表示为［16］

式中:Xk∈Rn为系统状态向量，Φk，k-1∈Rn×n为状态转移矩阵，Zk∈Rm为系统量测向量，Γk，k-1∈Rn×r为噪声驱动阵，wk∈Rr为系统噪声向量，Hk∈Rm×n为量测矩阵，vk∈Rm为量测噪声向量.

系统噪声和量测噪声符合:

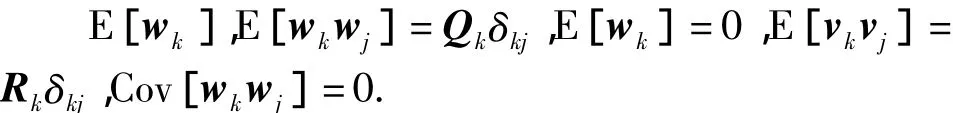
式中:Qk∈Rr×r为系统噪声阵，Rk∈Rm×m为观测噪声阵，δkj为 Kronecker-δ函数.

传递对准采用标准卡尔曼滤波方程［16］:

1.1 滤波池符号集构建

依据各种惯导误差方程，传感器误差方程、机翼模型、量测匹配方案，考虑空中、海上或是陆基对准情况，式(1)可以写成许多具体形式，即 Xk、Zk、wk、vk、Φk，k-1、Γk-1、Hk对应许多具体形式.

以符号来表示以上矢量和矩阵，则它们所有具体形式的并集为一个固定的符号集，而每种对准匹配方案即为从此符号集抽取的一个特定子集.根据符号类型不同，分成如下几类:

1)滤波状态符号说明.

包括:x、y、z向速度差，x、y、z向失准角，x、y、z向量测失准角，经度差、纬度差、高度差，x、y、z向角速率差，x、y、z向比力差，陀螺 向常值漂移，陀螺x、y、z向一阶马氏漂移，陀螺 x、y、z向刻度系数差，加计 向常值偏置，加计x、y、z向一阶马氏偏置，加计x、y、z向刻度系数差，x、y、z向机翼变形角，向机翼变形角速度.

2)滤波噪声符号说明.

包括:陀螺 x、y、z向常值漂移噪声，陀螺 x、y、z向一阶马氏漂移噪声，陀螺x、y、z向刻度系数噪声，加计 x、y、z向常值偏置噪声，加计 x、y、z向一阶马氏偏置噪声，加计x、y、z向刻度系数噪声，向机翼变形角噪声x、y、z向机翼变形角速度噪声.

3)滤波观测符号说明.

包括:x、y、z向速度，x、y、z向位置、经度、纬度、高度，俯仰角、横滚角、航向角，x、y、z向角速率，x、y、z向比力.

4)滤波矩阵元素符号说明.

矩阵 Φk，k-1、Γk-1、Hk由许多元素组成，其中每个元素为常数或多个符号运算的表达式.构成矩阵元素的符号分为如下几类:

①基本数学符号

包括:数字0～9、小数点、负号、四则运算符、幂运算符、左右括号.

②常用函数符号

③常量符号

椭球度e、基准重力加速度g0、圆周率PI、地球自转角速率、克拉索夫斯基规定地球椭球长半轴长Re.

④常用变量符号

变量符号包括:经度、纬度、高度，x、y、z向速度，俯仰、横滚、航向角，游移角，重力加速度，地球子午、卯酉圈主半径，火控 x、y、z向位置、速度，x、y、z向杆臂长度，x、y、z向机翼结构挠曲变形系数，导航系、载体系下x、y、z向角速率，导航系、载体系下x、y、z向比力，坐标变换矩阵，传感器相关时间等.

以上符号的名称、含义和初始值由数据库管理，可根据需要进行增删.

1.2 滤波池输入面板设计

具备了式(1)的各矢量及矩阵，再给出滤波式(2)的初始条件 X0、P0、Q0、R0，就可以启动实施对准滤波.因此，这里设计了滤波池输入面板，用于Xk、Zk、wk、vk、Φk，k-1、Γk-1、Hk、X0、P0、Q0、R0的输入、修改、保存、导入等操作.面板如图1所示.

图1 滤波池输入面板Fig.1 Input panel of filtering pool

首先，输入系统状态维数、噪声维数、观测状态维数;然后根据矢量维数来给出 Xk、Zk、wk、vk、X0、P0、Q0、R0逐项添加其参数，包括初始值、方差等，如图2所示.

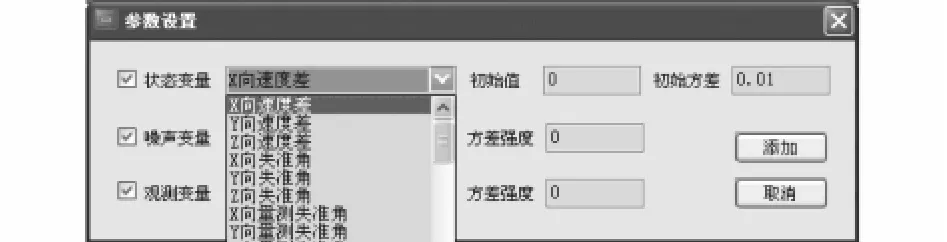
图2 滤波初始参数配置面板Fig.2 Initial filter parameter configuration panel

接着，依次利用矩阵输入面板给出 Φk，k-1、Γk-1、Hk的各元素.为了方便用户使用，设计了鼠标滑到某个符号上时给出提示的功能，如图1中下部分所示.

最后，将滤波匹配模型保存入数据库，例如，可命名“九维状态九维噪声速度+姿态对准匹配模型”滤波匹配模型库，当名称与数据库某一名称相同时，可选择是否覆盖之.另外，可用面板导入某一模型进行修改.

1.3 滤波池模型库设计

滤波池模型库用于保存2.2面板输入的滤波匹配模型，采用SQL Server2000数据库设计，模型库构成如表1所示.

表1 滤波池模型库Table 1 Model database of filtering pool

1.4 滤波池算法库设计

滤波池采用的滤波基本算法如式(2)，但在实际中式(2)的前提很难满足，有时需要增大系统噪声来近似处理.进一步的研究是设计更多的自适应滤波算法来扩展系统滤波功能.

常用的算法有Sage-Husa自适应滤波及其简化算法［14］，在式(2)中加入:

式中:

还可采用强跟踪自适应滤波算法［15］，即对状态方差阵Pk进行处理:

其中，sk+1=diag(s1(k+1)，s2(k+1)，…，sn(k+1))为状态方差预测阵的对角权重阵，由如下公式计算:

其中:Tr()为矩阵迹运算符，0≤ρ≤1为调节因子.

实际中，还有许多新近提出的自适应滤波算法.这里，采用动态链接库进行算法的编写，使得算法与滤波过程独立，且便于扩充.另外，滤波仿真前，需要模拟导航解算，其中也包含许多算法，也采用动态链接库设计.

1)算法动态链接库

算法动态链接库由头文件、实现文件和定义文件组成.

①头文件

用于给出导出函数命名，形式如下:

③定义文件

用于给出函数的导出列表，形式如下:

“LIBRARY(Navigation、Filter)

EXPORTS

(导航、滤波)函数1

(导航、滤波)函数2

……………………….

(导航、滤波)函数 n”.

2)算法数据库

算法数据库用于保存算法对应的函数信息，构成如表2所示.

表2 算法数据库Table 2 Algorithm database

1.5 滤波池功能类设计

1)文件读取类CGetFileData.

能够从数据文件中读出指定行、指定列数据，用于滤波计算和量测匹配等.

主要包括:函数StrToArray，用于将文件中一行数据按分割符拆分并存入字符串数组中;函数GetL-ineCount用于获取文件按总行数;函数GetColCount用于获取文件总列数;函数IsDataFile用于判断文件是否为数据文件;函数GetFile用于从指定文件中提取一定行列数据到二维字符串数组中.

2)矩阵元素提取类CGetStrData能够按照矩阵维数设定值将匹配模型中的矩阵字段按分割符拆分成单个矩阵元素.

主要包括:函数StrToArray，用于将矩阵字段值分成多行，将每行数据按分割符拆分并存入字符串数组中;函数GetStrData，利用字符串数组为对应矩阵元素赋表达式类型值.

3)表达式计算类CExpCal根据当前滤波时刻符号集中各符号数值对矩阵元素表达式进行计算.

主要包括:符号值提取函数GetSignValue，用于根据滤波迭代和导航解算的更新结果提取符号集分量值;函数CalFun，用于计算符号函数值;函数GetUnit，用于将运算单元保存到双向链表;函数Get-Node，用于提取表达式树状结点;函数GetNodeValue，用于计算节点值;函数AnalyzeExp，用于分析并表达式生成链表;函数CalExp，用于计算表达式值.1.6 滤波池执行流程设计

设计如图3所示的导航算法、对准匹配模型、滤波算法设置面板，从数据库中提取对应的函数和模型数据.

图3 滤波执行配置Fig.3 Executing configurtion of filtering

点击“确定”，进入如图4所示的滤波池执行流程.1)滤波仿真参数提取

滤波仿真参数包含子惯导开机时间、对准开始时间、主、子陀螺和加计的采样频率、主、子惯导的姿态、速度、位置解算频率、对准滤波频率.

2)惯导模拟导航

利用类CGetFileData提取主、子惯导导航参数，利用导航算法库首先对主惯导进行导航解算，然后在主惯导开机时刻，利用主惯导数据对其进行粗对准，进行子惯导模拟导航.

图4 滤波执行流程Fig.4 Executing procedure of filtering

导航解算动态链接库的使用步骤为:

①按算法库的函数参数定义导航算法函数

typedef void(_stdcall*NavFun)(参数列表).

②显示导入动态链接库

HMODULE hModule=::LoadLibrary(＂Navigation.dll＂).

③根据定义文件的函数索引提取导航函数

NavFun Nav=(NavFun)GetProcAddress(hModule，函数索引).

3)滤波器配置.

从模型库中提取滤波状态、噪声、观测量的符号、初始值、方差值、矩阵信息，利用类CGetStrData为各矩阵元素分配表达式.

4)匹配滤波.

在对准时间内，进行主子惯导匹配滤波.

①更新符号集数值，

②利用类CExpCal计算矩阵元素表达式数值，

③考虑主子惯导周期、延迟进行量测匹配，

④系统离散化，

⑤按照导航函数导入方法从滤波算法库导入滤波函数，执行当前滤波运算，

⑥输出当前滤波结果，重复步骤①～⑥.

2 Kalman滤波池性能测试

为了验证Kalman滤波池的工作性能，进行了6类30种对准匹配方案的滤波仿真试验，测试平台如表3.

表3 测试平台配置Table 3 Testing environment configuration

其中，6类对准匹配方案包括［2-12］:速度匹配、速度+姿态匹配、速度+位置匹配、比力匹配、角速率匹配、速度+角速率匹配.每类匹配方案包括几种具体的系统状态维数、噪声维数、滤波初始设置不同的对准匹配方案，例如速度匹配方案测试了:六维状态三维噪声小、中、大状态方差速度匹配方案、十二维状态三维噪声小、中、大状态方差速度匹配方案、六维状态六维噪声小、中、大状态方差速度匹配方案9种具体方案.实际中，状态初始值、系统噪声方差、量测噪声方差也可根据用户需要设置.仿真试验的条件为:初始经度 116°，纬度 40°，高度 3 000 m，初始轨迹速度500 m/s，初始姿态角为0;假设主惯导无误差;子惯导陀螺误差参数εbsb量级为0.1°/h，εbsw量级为0.01°/h;加速度计误差参数∇bsb量级为10-3g，∇bsw量级为10-4g;τg=τa=7 200 s;安装误差角 μbf各向均取为 1°;杆臂矢量为 LA=(5 m，-0.5 m，-1 m).

机翼挠曲变形采用2阶马尔科夫［7］过程模拟，三向结构挠曲变形系数为 βx=4，βy=5，β=6，方差为 E［ηηT］=0.1δkj;机翼颤振变形幅度为 Ay=Az=0.001 m，颤振频率为 fy=fz=40 Hz.

仿真时间20 s，滤波周期0.5 s，主子惯导姿态、速度、位置解算周期0.01 s.

通过记录测试过程及结果信息，得具体参数如表4.

表4 传递对准Kalman滤波池性能测试结果Table 4 Performance testing result of Kalman filtering pool

测试结果表明:传递对准Kalman滤波池运行稳定、占用系统资源较小、存储容量小、修改方便，且具有较高的计算精度和运行速度.

3 结束语

本文设计了一种应用于传递对准数字仿真系统的通用Kalman滤波池，进行匹配方案、滤波算法研究.滤波池采用VC++6.0平台和SQL Server 2000数据库系统开发，通过符号集、操作面板、C++功能类、模型算法数据库、算法动态链接库的设计，使得用户能够灵活方便地进行任意匹配方案、状态方程、量测方程、滤波参数、滤波算法的研究.仿真测试验证了滤波池稳定性、灵活性，表明其占用系统资源少、存储容量小，具有较高的计算精度和运行速度，有效提高了传递对准匹配方案及滤波算法的研究效率，为机载导弹捷联惯导系统设计和传递对准的有效实施提供理论和技术参考.另外，此滤波池可以很容易地修改应用于其他滤波领域.

［1］王司，邓正隆.惯导系统动基座传递对准技术综述［J］.中国惯性技术学报，2003，11(2):61-67.

WANG Si，DENG Zhenglong.Technique review of transfer alignmentfor inertial navigation systems on moving base［J］.Journal of Chinese Inertial Technology，2003，11(2):61-67.

［2］KAIN J E，CLOUTIER J R.Rapid transfer alignment for tactical weapon applications［C］//Proceedings of the AIAA Guidance，Navigation and Control Conference. Boston:MA，1989:1290-1300.

［3］ROGERS R M.Velocity-plus-rate matching for improved tactical weapons rapid transfer alignment［C］//AIAA Guidance，Navigation and Control Conference.UNJ SA，1991:1580-1588.

［4］SHORTELLE K J，GRAHAM W R.F-16 flight test of a rapid transfer alignment procedure［C］//IEEE PLANS.Ft.Lauderdale:FL，1998:379-386.

［5］LYOU J，LIM Y C.Transfer alignment error compensator design based on robust state estimation［J］.Transactions of the Japan Society for Aeronautical and Space Sciences，2005，48(61):143-151.

［6］LYOU J，LIM Y C.Transfer alignment considering measurement time delay and ship body flexure［J］.Journal of Mechanical Science and Technology，2009，23(1):195-203.

［7］俞济祥.惯性导航系统各种传递对准方法讨论［J］.航空学报，1988，9(5):211-217.

YU Jixiang.Discussion on several transfer alignment methods of inertial navigation system［J］.Acta Aeronautica et Astronautica Sinica，1988，9(5):211-217.

［8］黄昆，单福林，杨功流，等.舰载角速度匹配传递对准方法研究［J］.中国惯性技术学报，2005，13(4):1-5.HUANG Kun，SHAN Fulin，YANG Gongliu，et al.Angular rate matching method for shipboard transfer alignment［J］.Journal of Chinese Inertial Technology，2005，13(4):1-5.

［9］卢松华，罗建军，岳晓奎.速度+方位角匹配传递对准算法的简化与仿真［J］.弹箭与制导学报，2005，25(3):292-295.

LU Songhua，LUO Jianjun，YUE Xiaokui.Simplification and simulation of velocity-plus-azimuth matching T/A［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25(3):292-295.

［10］陈凯，鲁浩，闫杰.传递对准中一种新的姿态匹配算法［J］.西北工业大学学报，2007，25(5):691-694.

CHEN Kai，LU Hao，YAN Jie.A different and better algorithm for attitude match of transfer alignment［J］.Journal of Northwestern Polytechnical University，2007，25(5):691-694.

［11］于飞，翟国富，李倩，等.速度加角速度匹配传递对准方法研究［J］.传感器与微系统，2009，28(6):69-72.

YU Fei，ZHAI Guofu，LI Qian，et al.Research on velocity plus angular rate match transfer alignment［J］.Transducer and Microsystem Technologies，2009，28(6):69-72.

［12］李群生，董景新，鲁浩.角速度匹配在机载武器传递对准中的应用［J］.弹箭与制导学报，2009，29(3):62-64.

LI Qunsheng，DONG Jingxin，LU Hao.The application of angular rate matching to transfer alignment for airborne weapons［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29(3):62-64.

［13］SPALDING K.An efficient rapid transfer alignment filter［C］//Proc of the AIAA GN＆C Conference.Montreal，Canada，1992:1276-1286.

［14］鲁平，赵龙，陈哲.改进的Sage-Husa自适应滤波及其应用［J］.系统仿真学报，2007，19(15):3503-3505.

LU Ping，ZHAO Long，CHEN Zhe.Improved Sage-Husa adaptive filtering and its application［J］.Journal of System Simulation，2007，19(15):3503-3505.

［15］张诗桂，朱立新，赵义正.粒子滤波算法研究进展与展望［J］.自动化技术与应用，2010，29(6):1-16.

ZHANG Shigui，ZHU Lixin，ZHAO Yizheng.The development and prospect of particle filtering algorithm［J］.Automation Technology and Application，2010，29(6):1-16.

［15］付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003:25-28.

FU Mengyin，DENG Zhihong，ZHANG Jiwei.Kalman filtering theory and its application in navigation system［M］.Beijing:Science Press，2003:25-28.