时间序列部分周期模式的更新算法

王晓晔，肖迎元，张德干

(1.天津理工大学智能计算及软件新技术重点实验室，天津300191;2.天津理工大学计算机视觉与系统省部共建教育部重点实验室，天津300191)

时间序列部分周期模式的挖掘是一类重要的数据挖掘任务，在许多场合都有重要的应用，如电力负荷时序数据的高峰期往往具有部分周期性，发现这种周期就可以避开高峰用电，减轻电厂的负担.

对于时间序列数据挖掘的研究主要集中在相似性问题和时态模式挖掘的研究［1-2］.其中相似性问题研究主要是面向查询的需要［3-4］，包括各种相似性搜索算法［1］的研究.时态模式挖掘则主要包括各种序列的模式挖掘，进行时态因果、周期模式、关联规则和重要事件的预测［5］等内容.

在时态模式的挖掘方面，从时间序列中抽取模式是一个比较新颖的方向.从研究内容来分，目前研究重点主要集中在2个方面:对时序中的事件出现加以模式发现和预测，如时态因果和关联规则;挖掘时序数据的周期模式，包括全周期模式和部分周期模式.部分周期模式的研究大多采用了Apriori-like启发式挖掘算法的思想和理论.

由于Apriori-like不能发现不同周期之间的模式和计算复杂度过大等，文献［6］提出了一种对单周期和多周期都适用的部分周期模式挖掘算法:最大子模式迎合树算法(the max-subpattern hit set tree，Mht).但是该算法只能对现有时间序列数据库进行挖掘，不能进行在线部分周期模式的挖掘.文献［7］在此基础上提出了一种增量式的在线挖掘算法，可以根据新增的数据对最大子模式树进行调整，但是由于数据量会越来越大，因此总的计算量还是很大的.

文中提出了一种带移动窗的部分周期模式挖掘算法，由于在某些应用场合数据的分布特性会随着时间的变化而有所变化，所以从较早的数据中提取的模式已经不能反映现有数据所隐含的模式.因此只要求对近期的时间序列数据进行挖掘，每次挖掘过程都是在最近的时间窗口［8］中进行，所挖掘的模式反映了最新的数据集中的知识.本算法对最新窗口中的数据搜索次数不多于2次，因此计算量要大大降低，非常适用于大型时间序列数据库的挖掘.

1 时间序列的部分周期模式

1.1 问题定义

假设一个含有n个时间标记的特征序列，对于每个时刻i，Di为该时刻的特征值(由原始时间序列导出)，特征序列的所有特征集定义为L，因此特征时间序列可以表示为

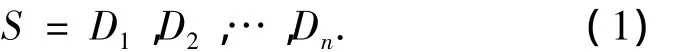
例如对于某支股票的原始时间序列，是以天为单位记录该股票的收盘价，则每个时间点的数据为具体的数值，因此需要将其量化为某些特征值(如高、中、低等)，然后用一系列字母来表示，则量化所得特征集 L 可以表示为{a，b，c，…}.

定义1 模式是一个非空序列s=s1，s2，…，sp，长度p叫做模式的周期，对于∀i，si是一个特征集(若该特征集只包含一个字母，则省略集合符号，如{a}可以写成a，具有j维特征的模式也可以叫做j-模式，在模式中允许符号“*”出现，它表示可以与任意单个字母相匹配.

定义2 如果模式s'=s1'，s2'…，sp'与s具有相同的长度，且对于∀i，si'⊆si，则称模式 s'为模式 s的子模式.

如对于模式 a{b，c}*{a，c}f，第 2 个位置可以是b或c，它是一个长度为5的模式，即周期为5，而模式中含有4个字母，因此又叫做4-模式.显然模式ac*cf和a＊＊cf是模式a{b，c}*{a，c}f的子模式，而模式ab*ac不是它的子模式.由定义可知，任意模式的特征维数要大于或等于它的子模式的特征维数.

定义3 一个特征时间序列S形式如式(1)所示，可以被分割成长度相等(长度为p)相互独立的模式，则 S=S1，S2，…，Si，…，其中 Si=Dip+1，…，Dip+p，i=0，…，［n/p］-1，则每个模式 Si叫做一个周期段，其周期为p.

如果一个周期段Si是模式s的子模式，则称周期段Si与模式s相匹配.

定义4 一个模式s在某个特征时间序列中的频率值是指这个时间序列中与模式相匹配的周期段的个数，记作frequency_count(s).显然若时间序列有m个周期段，则频率值应小于m，在极端情况下(所有周期段都与该模式匹配)等于m.

定义5 一个模式s在某个特征时间序列中的置信度是指它在该模式中的频率值与周期段数m的比值，记作confidence(s).则

定义6 如果一个模式在特征时间序列中的置信度不小于某个阈值(该阈值记作min_conf)，则称这个模式是频繁部分周期模式，j维频繁部分周期模式集简称为j-频繁模式集，记作Fj.

1.2 部分周期模式挖掘

部分周期模式挖掘算法基于文献［6］中提出的最大子模式迎合树算法(Mht).算法中通过扫描特征时间序列构建了一个叫做最大子模式的树T(如图1所示)，树上的节点代表了时间序列的所有候选频繁模式.子节点是父节点的子模式，由子模式的定义知，子节点的特征维数要小于父节点的特征维数.因此当将父节点的某个字母用*代替时，将形成子节点，由图中可知子节点和父节点之间的连接用被取代的字母所标识.构建最大子模式树的关键是产生根节点，它在所有候选频繁模式中特征维数最大，因此叫做最大模式Cmax.Cmax由1-频繁模式集F1的所有元素合并而产生.2个模式s和t的合并操作定义为(s∪t)i=si∪ti.如模式 a*bc*与模式bc*r*合并的结果为模式{a，b}cb{c，r}*，若F1={a＊＊，*b* ，*c* ，＊＊d}，则 Cmax=a{b，c}d.

树的子节点的生长是将Cmax与时间序列中的周期段进行求交集时所产生的迎合(hit)的过程.迎合是指 Cmax与周期段的交集，如果 Cmax=a{b，c}d，Si=aba，则他们的迎合为ab*，若树中没有此节点，则在其相应的父节点下面增加该节点，此节点与父节点之间的连接用它与父节点相匹配所错失的字符来标识，并将此节点的迎合值置为1，若此节点已经存在，则将它的迎合值加1，图1中迎合值标注在该节点的旁边，是该节点所代表的模式的迎合次数值(简称迎合值).很显然，某个节点的迎合值并不是它的频率值，因为在它的所有隐含祖先节点中都包含有该节点所代表的模式(如图1中虚线所连接的都是隐含的父子节点关系)，如模式*bd的直接父节点是*{b，c}d，隐含父节点是 adb，祖先节点是a{b，c}d，当然隐含父节点往往不止1个，因此求取模式*bd的频率值需要加入它的所有祖先节点的迎合值(即10+0+12+20).树中的节点构成了候选频繁模式集，当某个节点的频率值大于min_conf×m时，则认为该节点所代表的模式是频繁模式.

图1 最大模式树举例Fig.1 Example of max pattern tree

Mht算法的实现步骤如下:

1)给定周期p，将特征时间序列S分割成长度为p的一系列周期段S1，S2，…，Sm，m为周期段的段数.

2)扫描所有的周期段，得到所有的1-模式集L1及每个模式的频率值，将频率值不小于min_conf×m的1-模式抽取出来组成1-频繁模式集F1.

3)将F1的所有元素合并，产生Cmax.

4)重新扫描所有周期段，求取周期段与Cmax的交集，若所得到的模式已经存在，则将节点的迎合值加1，否则在相应的父节点下插入新的节点(若它的祖先节点不存在，则插入祖先节点，并将祖先节点的迎合值置0)，将新节点的迎合值置1.树的叶节点应该含有2个非*字母，因为已经有1-频繁模式集仅含有1个非*字母.

5)将每个节点的迎合值与它的所有隐含父节点的迎合值相加，得到该节点的频率值，若某个模式的频率值不小于min_conf×m，则该节点所代表的模式为频繁模式.

2 带移动窗的的部分周期模式挖掘算法

某些时间序列挖掘过程中只要求在近期数据库中进行，因此在挖掘过程中引入时间窗口的概念，时间窗口［8］是指在某个时间区域之前的时间序列数据都是过时的，不用于当前部分周期模式挖掘过程的，即部分周期模式的挖掘过程只是在当前时间区域中进行，提高了挖掘结果的时效性.

令当前时间窗口为Cur_window，起止时间为Ttart和Tend，SC为当前时间窗口中的特征时间序列，D为周期段的段数，F为SC中的频繁模式集.从时间Tend到Tnow为时间序列新增的数据，新数据集合为sc，d为sc的周期段的段数，则新时间窗口 New_window的起止时间为 Tstart+(Tnow-Tend)和 Tnow.在Tstart和Tstart+(Tnow-Tend)之间的数据为老数据应淘汰，记为retire，周期段数为 r，则新时间窗口New_window的时间序列记为NewSC，NewSC=SC∪sc/retire.模式 X 在 SC、retire、sc和 NewSC中的频率值记为X.frequencyS、X.frequencyr、X.frequencys和 X.frequencyN.

经过时间序列数据库的更新，在新时间窗口中的1-模式存在4种情况:

1)1-模式在Cur_window和New_window都是非频繁的即 X.frequencyS＜min_conf×D，且 X.frequencyN＜min_conf(D+d-r).

2)1-模式在Cur_window和New_window都是频繁的即 X.frequencyS＞min_conf×D，且 X.frequencyN＞min_conf×(D+d-r).

3)1-模式在Cur_window是频繁的，而在New_window中是非频繁的即X.frequencyS＞min_conf×D，但X.frequencyN＜min_conf×(D+d-r).

4)1-模式在 Cur_window是非频繁的，而在New_window中是频繁的即 X.frequencyS＜min_conf×D，但X.frequencyN＞min_conf×(D+d-r).

显然，只需考察3)和4)2种情况即可.

MW算法包括2步:

1)根据频繁1-模式集的更新算法对F1集进行更新产生F1';

2)由 F1'合并产生的最大模式为 C'max，若C'max=Cmax，则保留原来的树T，只需更新各节点的迎合值即可.考虑淘汰的时间序列retire的周期段，求取与C'max的交集，若所得到的模式存在，则将相应节点的迎合值减1;考虑新增时间序列sc的所有周期段，求取与C'max的交集，若所得到的模式存在，则将相应节点的迎合值加1;

若C'max≠Cmax，则采用更新算法MTU对最大子模式树进行更新;

下面分别介绍频繁1-模式集的更新算法和最大子模式的树的更新算法MTU.

2.1 频繁1-模式集的更新算法

1)遍历淘汰数据库retire，计算所有的模式X∈F1在retire中的频率值X.frequencyr;遍历新增数据库sc，计算所有的模式X∈F1在sc中的频率值X.frequencys，从而得到F1的所有模式在NewSC中的频率值，X.frequencyN=X.frequencyS+X.frequencyS-X.frequencyr.若 X.frequencyN＜ min_conf×(D+d-r)，则将其淘汰，否则保留.

2)在遍历retire和sc的同时，根据sc的每一个周期段构造不在F1中的候选1-模式集C1，对C1中的任一模式Y，若Y.frequencyS＜ min_conf×(d-r)+Y.frequencyr，依据文献［7］中的引理2，那么 Y 在更新后序列中就必是非频繁的，可将其从C1中删除.

3)对原部分时间序列SC/retire进行遍历，计算C1中各个候选 Y在 SC/retire中的频率值，加上Y.frequencyS，便得到Y在更新后时间序列NewSC中的频率值Y.frequencyN，若Y.frequencyN不低于min_conf×(D+d-r)，则Y为频繁模式，从而得到新的频繁模式集F1'为保留的F1和C1中的频繁模式的集合.

2.2 最大子模式的树的更新算法

假设C'max为更新后的最大模式，显然C'max由更新后的1-频繁模式集F1'的所有元素合并而产生.若cj为Cmax第j个位置特征值符号，cj'为C'max第j个位置特征值符号，如果cj≠cj'，则cj将被更新为cj'.更新过程分 2 步［7］，即先删除 cj，形成 Ctmax，然后在相应位置增加cj'形成C'max，记录F1与F1相比较有所更新的1-模式集记为U1.

同样，相应的最大子模式树的更新过程也分为2步:1)更新是生成树Tt，它的根节点是，很显然是Cmax的子模式，因此，如果在T中有节点代表了，则这个节点变成Tt的根节点，否则，创造一个新的节点.考虑图1的树，若C'max=a{b，e}d，则=abd，abd以及它的直接后代节点ab*便是初始的Tt，而此时树Tt还不完整，需要加上它所有的非直接的后代节点，以及相应的迎合值，扫描树T，对于树T的每一个节点，求它与的交集，然后将所得节点连同其在T中的迎合值插入树Tt中(若该节点已存在，则将迎合值累加).则在树Tt中加入如下模式:abd(10+12)，*bd(0+20)，a*d(50+10)，ab*(8+32).结果如图2所示，同时考虑淘汰的时间序列retire，只需求取那些不包含 U1中的1-模式的周期段与的交集，若所得到的模式存在，则将相应节点的迎合值减1.

图2 插入所有后代节点后的树TtFig.2 Tree Ttafter inserting all the posterity node

显然，含有新增字符的子模式的迎合值不能确定.同时一些其他的新模式或许会出现，如模式aed，因此需要重新搜索时间序列.对原部分时间序列SC/retire进行遍历，只需求取那些包含U1中的1-模式的周期段与C'max的交集，若所得到的模式已经存在，则将节点的迎合值加1，否则在相应的父节点下插入新的节点(若它的祖先节点不存在，则插入祖先节点，并将祖先节点的迎合值置0)，将它的迎合值置1.搜索新增时间序列sc的所有周期段，将它与Cmax'的交集加入树T'中，过程如上述.

3 计算复杂度分析

本文提出的MW算法，对于长度为D+d的时间序列，扫描次数最多为2次.在第1)步中的工作主要是检查F1中的频繁模式是否保持频繁，是在对sc和retire进行1次搜索完成的，同时对sc构造出的候选集C1进行修剪，搜索Sc/retire，从C1中发现新的频繁1-模式.总共在1)对Sc+sc搜索了1次，但是由于算法计算很简单，因此计算量很小.在2)中，若C'max=Cmax，则只需对retire和sc搜索1次，只有在C'max≠Cmax时，才需要对当前时间窗口Sc和新增窗口sc进行搜索，而且对Sc进行搜索时，只是对某些符合条件的周期段进行搜索，因此在第2)步中，最坏的情况下搜索1次，关于最大子模式树的构建中计算复杂度分析见文献［5］.

4 算法测试及结果分析

在实验中使用2个数据库进行实验，其中一个是人工合成数据库，用一个随机时间序列生成器产生所需的1 000 000个含有4个特征值的时间序列数据.另一个是某城市某个主干道某检测面的交通流量检测数据，其检测间隔为5 min，数据库大小为12 M，截取的数据片度如图3所示，其中的连续数据通过行业专家的经验被量化为5个等级:很小、小，中等、大和很大.

图3 交通流量数据Fig.3 Traffic flow data

实验中分别将增量长度d和置信度阈值min_conf作了变化，其周期分别定为4和24.算法实现采用Matlab编程工具，运行机型为赛扬M，1.46GHz的主频，256M内存的PC机，为分析其计算效率，结果如下.实验发现，当周期为24时，可以得到明显的符合实际的周期模式.而由于周期为4时，周期过短而造成无法很好的识别部分周期的结果.

表1 在人工合成时间序列上的运行结果Table 1 Run time on the synthetic data

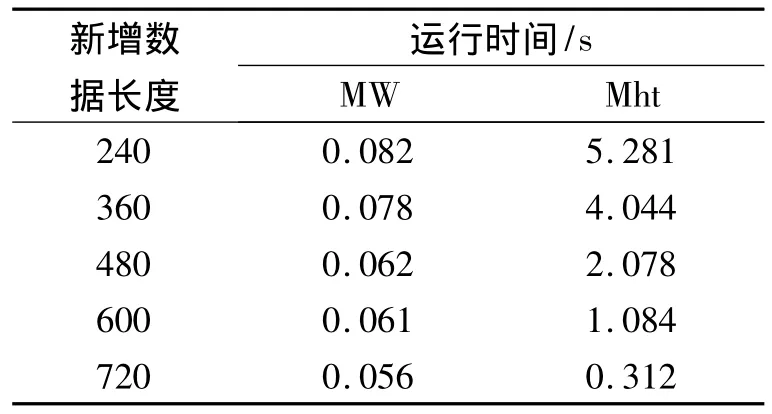
表2 在交通时间序列上的运行时间比较Table 2 Run time on the traffic time series data

表1和表2分别给出了当窗口长度分别固定为2 000和2 400，min_conf=30%时，2种算法在合成时间序列和交通流时间序列中的运行时间比较.由表中可以发现，本文所提出的基于移动窗的MW算法所用的时间要比最大子模式迎合树Mht算法要少的多，而且MW算法的运行时间几乎不随新增数据长度的变化而变化，对于大型时间序列数据运行时间比较稳定，这是因为MW算法每次的计算对象都是新窗口中的数据，而且当新窗口中的1-模式没有变化时，则不需要对最大子模式树的结构进行更新.而Mht算法随着新增数据长度的增长运行时间而减少，这是因为在总的数据长度不变的情况下，增加新增数据的长度将会减少最大子模式树总的更新次数，从而降低了计算时间.因此，MW算法更适合于大型时间序列数据.

图4 当min_conf值变化时的运行时间Fig.4 The run time when min_conf change

为说明置信度阈值对计算时间的影响，图4给出了当窗口长度D=2 000和新增数据长度d=200，而改变置信度阈值min_conf时，2种算法对于合成时间序列的计算时间比较结果.由图4可见，2种算法随着置信度阈值的增大，计算时间都在减小，这是因为随着置信度阈值的增大，1-频繁模式越来越少，因此总的计算量也越来越小，而且当置信度阈值超过50%时，计算时间变化会很小，这是因为此时，满足条件的1-频繁模式很少，而且变化不大，从而使得不必进行过多的计算.

5 结束语

提出了一种带移动时间窗的时间序列部分周期模式挖掘算法.在挖掘过程中数据不断的被采集，数据的性能分布也会有相应的变化，为了挖掘最新的模式，利用移动时间窗，在先前挖掘结果的基础上，对最近的时间序列进行部分周期模式挖掘.文中提出的算法最多对指定时间窗口中的数据搜索2次即可.既保证了挖掘结果的时效性又降低了算法的计算复杂度.实验中在各种条件下，对算法进行了不同侧面的比较，搜索速度加快，使得该算法更适用于大型时间序列数据库的部分周期模式挖掘.

［1］RODDICK J F，SPILIOPOULOU M.A survey of temporal knowledge discovery paradigms and methods［J］.IEEE Trans on Knowledge and Data Engineering，2002，14(4):750-767.

［2］HU X，XU P，WU Sh，et al.A data mining framework for time series estimation［J］.J Biomed Inform，2010，43(2):190-199.

［3］LIAN X，CHEN L.Efficient similarity search over future stream time series［J］.IEEE Trans on Knowledge and Data Engineering，2008，20(1):40-54.

［4］MARTEAU P F.Time warp edit distance with stiffness adjustment for time series matching［J］.IEEE Trans On Pattern A-nalysis and Machine Intelligence，2009，31(2):306-318.

［5］RICHARD J.POVINELLI XIN F.A new temporal pattern identification methord for characterization and prediction of complex time series events［J］.IEEE Trans on Knowledge and Data Engineering，2003，15(2):339-352.

［6］HAN J，GONG W，YIN Y.Efficient mining of partial periodic patterns in time series database［C］//Proc 15th Int'l Conf Data Eng Sydney，Australia，1999:106-115.

［7］AREF W G，ELFEKY M G，ELMAGARMID A K.Incremental，online，and merge mining of partial periodic patterns in time-series databases［J］.IEEE Trans on Knowledge and Data Engineering，2004，16(3):332-342.

［8］欧阳为民，蔡庆生.基于时间窗口的增量式关联规则更新技术［J］.软件学报，1999，10(4):427-429.

OUYANG Weimin，CAI Qingsheng.A Time-window based incremental technique for updating association rules［J］.Journal of software，1999，10(4):427-429