应用VOF方法的水平圆柱入水数值模拟

陈宇翔，郜冶，刘乾坤

(哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001)

物体入水现象如船舶航行砰击、水上飞机降落、空投鱼雷入水及垮塌桥梁落水广泛存在于自然界.物体入水问题是典型的非线性问题，其入水过程特别是初始瞬间物体会受到巨大的冲击载荷，以风浪中航行的船舶为例，船体砰击会造成船体的震动、减缓船速，严重的话还会导致结构损坏;空投入水的鱼雷则可能因为入水冲击造成鱼雷结构损坏、弹道失控等严重问题.物体入水问题在现代许多军事及民用领域的广泛存在及其重要性激发了众多科学家及工程人员的研究热情［1］.因为圆柱、楔等形状结构简单，常可作为所需研究物体的简化外形，所以研究者们常常以它们作为研究对象.20世纪90年代早期以前，大部分的研究者［2-4］均基于势流理论假设研究过楔等形状物体的入水问题.然而，边界元方法在处理复杂自由表面问题方面不够强健［5］.自1981年Hirt与 Nichols［6］等提出 VOF方法以来，带自由表面的两相粘性不可压缩流体运动的数值计算技术得到了迅速的发展.近30年来，VOF方法在数值计算物体入水领域得到了广泛的应用.Arai［7］假设流动为无粘不可压流动，应用VOF方法对二维楔、圆柱、船艏的砰击入水问题进行了模拟;Schumann［8］用类似的方法模拟了艏的砰击入水.Xing-Kaeding［9］基于VOF方法，应用Comet软件对二维水平圆柱的粘性不可压出入水运动进行了模拟，取得了与实验结果符合较好的结果.本文应用Fluent软件中的VOF方法结合动网格技术对二维圆柱的入水问题进行了数值模拟计算，实现了圆柱运动的刚体动力学方程和气液两相流动的N-S方程的耦合求解.本文数值模拟计算结果与Greenhow和Lin［10］的实验对比表明，圆柱入水的重要现象如飞溅现象、空气垫效应［11］等自由表面形状的变化得到了很好的呈现，圆柱运动轨迹得到了很好的追踪.同时，还对粘性对圆柱入水运动问题的影响进行了研究.

1 问题的描述及数值水池的建立

如同文献［10］中Greenhow和Lin设计的实验，一个直径11 cm的零浮力(neutral buoyancy)水平圆柱由静水上方某一确定位置自由落体进入水池中.而且当圆柱在接触水面的瞬间，其速度为3.13 m/s，随后圆柱继续向下运动直至到达水深为30 cm处.

由以上描述的问题，本文建立了一个宽60 cm，高60 cm(水深30 cm)的二维数值水池.为准确地捕捉圆柱入水冲击引起的自由表面变化等重要现象，整个计算区域采用正交四边形网格，为此在圆柱边界采用阶梯近似［12］处理，并对圆柱附近的网格进行了加密处理，见图1.圆柱边界应用无滑移壁面边界条件，水池上边界应用压力出口边界.为了节省计算网格并尽可能模拟真实流动区域，采用文献［9］中的方法，水池的左右边界(包括静水和空气区域)应用UDF定义边界条件使压力保持为自由表面未变化前的静压;水池下边界应用速度为零的速度入口边界条件.

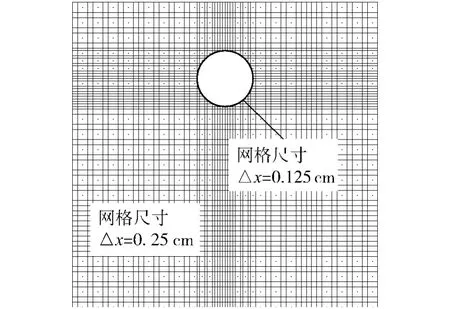
图1 圆柱入水问题计算网格Fig.1 Numerical grid for the circular cylinder waterentry case

2 理论基础和计算方法

圆柱入水问题是复杂的两相流体流动和固体运动的耦合过程.圆柱的入水冲击会突然改变两相流场中水的压力场和速度场，而流场的改变同时又会反作用来影响圆柱的运动.本文中，有限体积法被用于计算存在自由表面的粘性不可压两相流体流动;二维圆柱视为刚体，其在落水过程中为一自由度(1DOF)运动，流场形状随时间变化，需要应用动网格.

2.1 流体流动与刚体运动方程

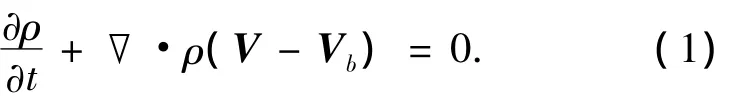
式中:V是流体运动速度矢量，Vb是有限体积即网格单元表面的运动速度.动量方程为

对于每一个有限体积单元，连续性方程为

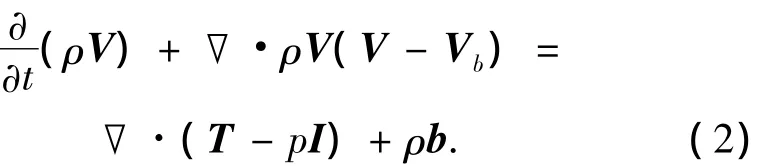
式中:T为粘性应力张量，I为单位张量，b为体积力矢量.当网格单元移动或改变形状时，有限体积单元满足空间守恒律:

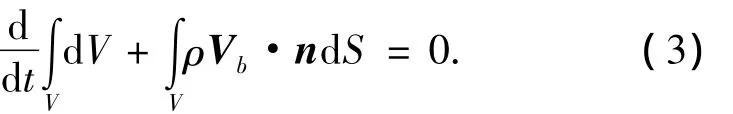
由于自由表面的形状和位置是未知的，需要由求解过程给出，因此数值求解带自由表面的两相流动问题变得十分困难.为了模拟有自由表面的两相流流动，本文应用VOF(volume of fluid)方法.VOF是一种捕捉自由表面的方法，它同时对水和空气建立控制域，通过求解附加的方程来捕捉自由面，这种方法在处理复杂的自由表面流动问题具有很大优势.引入的附加体积分数输运方程:

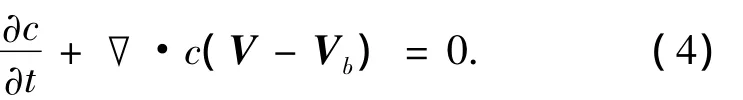
式中:c=Vl/V为液相体积分数.VOF方法将0＜c＜1的两相混合流体处理为单相流，认为其有同样的压力和速度值.其物性参数如密度处理为

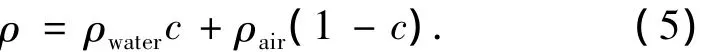
由牛顿第二定律，流体中运动的圆柱刚体动力学方程为

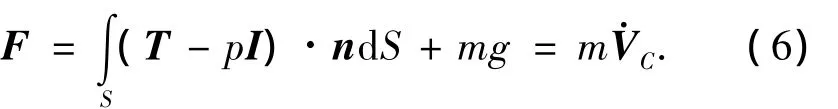
式中:VC为运动时的圆柱重心的速度矢量.

2.2 网格运动方案

为了适应由于圆柱的刚体运动而不断改变的流场形状，需要应用动网格模型.为了获得很好的数值解，特别是在对于圆柱入水冲击引起的的强非线性自由表面变化模拟的情况下，需要很好的网格质量，因此本文采用整体网格移动而不变形的方案［13］.本文应用Fluent的动态层模型，由定义整个流动区域和圆柱为刚体区域，而将数值水池上下边界定义为静止区域来实现网格整体运动而不变形.每一当前时间步的网格运动速度为上一时间步网格速度与当前时间步圆柱所受的两相流体压力、粘性力以及自身重力所引起的速度增量之和.

2.3 计算方法

本文中，PISO算法用来耦合速度场和压力场;VOF两相流模型的自由面重构方法用来捕捉自由表面的变化情况;对于流场中的湍流的描述则采用标准k-ε两方程模型和壁面函数法;压强差值采用PRESTO!差分格式.

3 计算结果及分析

本文应用之前描述的Fluent动网格技术结合VOF方法对二维零浮力水平圆柱入水问题进行了计算，对比分析了数值计算结果与实验结果，并且对于粘性对圆柱入水运动的影响进行了分析.

3.1 自由表面的变化

圆柱入水的瞬间，改变了其周围压力等流场参数，圆柱的速度突然下降，而同时与其接触的水相应地被突然加速，在圆柱两侧激起两股射流，射流向斜上方上升直至其变得不稳定.由于重力的影响，随着时间的发展，射流形状由直线逐渐弯曲向下.

图2 零浮力圆柱入水自由表面变化:实验(左)和数值(右)结果对比Fig.2 Free surface deformation of a neutrally buoyant cylinder water-entry:simulation(right)and experiment(left)

在圆柱入水的过程中，一些空气也随同圆柱一起被压入水中，会形成所谓的＂空气垫＂.由于圆柱底部倾角较大，导致底部的空气逃逸较多，可压缩空气垫主要存在于圆柱两侧，将圆柱两侧表面与水隔开，随着圆柱入水深度的不断增加，空气不断排出，圆柱的沾湿面积不断增加.

为了方便比较观察实验照片和数值计算结果，图2给出了5个不同时刻实验和数值模拟的水池自由表面变化情况对比图.由图2可知，本文计算的零浮力圆柱入水过程自由表面变化情况和实验对比符合很好，成功地模拟显示了圆柱入水冲击引起的水射流形成、行进、弯曲以及入水圆柱周围的空气垫等自由表面的变化现象.

3.2 圆柱的刚体运动

进入水池之前，圆柱在空气中自由下落，在气流场中受到的阻力较小.圆柱接触水面的瞬间，两相流场中的水由于圆柱的冲击被大大加速，压力场、速度场特别是圆柱附近的压力分布突然改变.相应地，圆柱受到流场很大的阻力(包括压差阻力、摩擦阻力)，速度大大降低.图3给出了圆柱入水过程的无量纲阻力(流场数据积分得到的入水阻力与重力的比值)与时间的关系，零时刻圆柱受到很大的一个冲击力，而随着时间的进行，进入水中的圆柱周围的压力分布逐渐均匀，圆柱速度越来越慢，阻力的变化逐渐平缓.

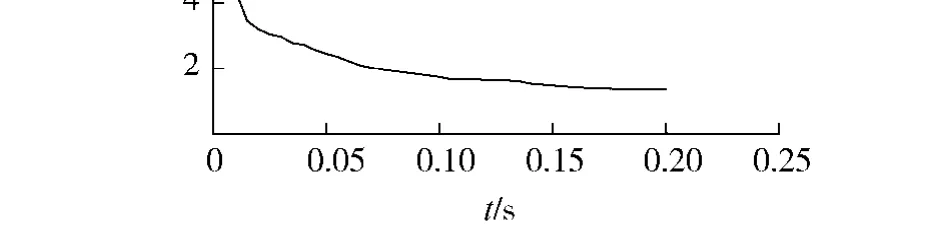
图3 圆柱入水过程的无量纲阻力时间曲线Fig.3 Time histories of non-dimensional drag force during cylinder water-entry

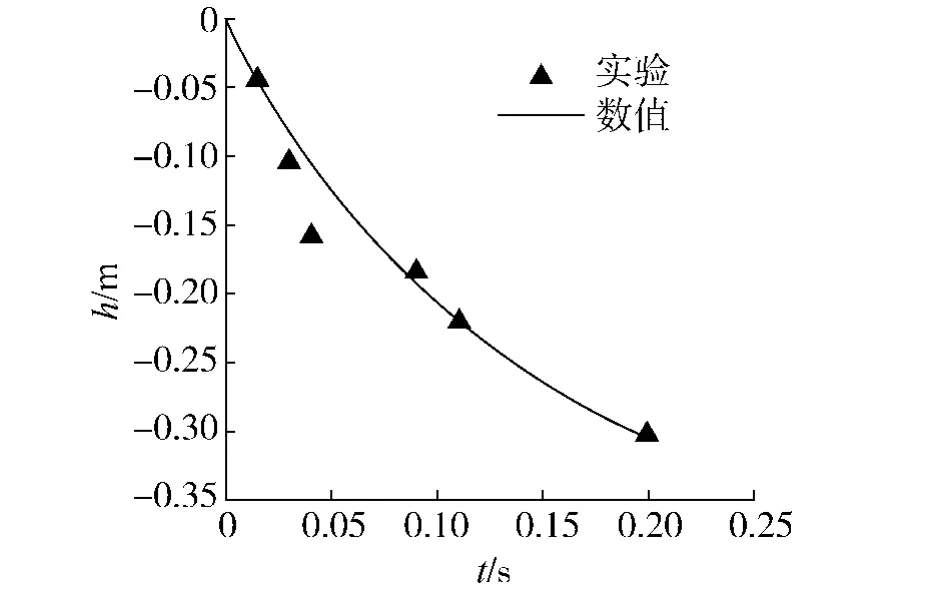
图4 圆柱竖直运动时间曲线Fig.4 Time histories of vertical motion of the cylinder

图4给出了圆柱入水过程没入水中的圆柱位置(y轴坐标为入水后圆柱底部最低点的位置)和入水时间关系曲线，随着圆柱在水中的下降，圆柱受到的阻力不断减小，速度也逐渐降低，因此圆柱位置的变化曲线也逐渐平缓.由图4中的曲线与实验记录的数据点对比可知，数值解同样和Greenhow和Lin的实验相当吻合(图中偏差较大、标记问号的一个点同时也是实验中认为存在问题的数据点).

3.3 粘性对入水圆柱运动的影响

由于水的粘性，入水过程中圆柱除了受到由于两相流场的压力场分布不均带来的压差阻力，还受到粘性引起的摩擦阻力.

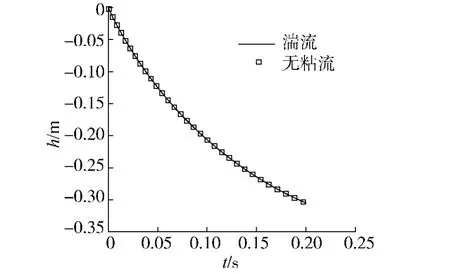
图5 圆柱入水竖直运动过程时间曲线(湍流和无粘流)Fig.5 Time histories of vertical motion of the cylinder during cylinder water-entry(turbulence and without turbulence model)

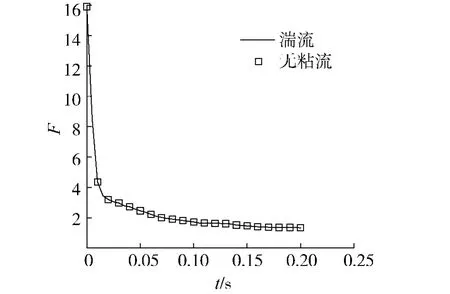
图6 圆柱入水过程的无量纲阻力(湍流和无粘流对比)Fig.6 Time histories of non-dimensional drag force during cylinder water-entry(turbulence and without turbulence model)

为了考察粘性对圆柱入水问题的影响，本文计算了无粘流模型下的圆柱入水过程，并与之前基于湍流模型的数值计算结果进行比较.图5、6分别给出了基于湍流模型和无粘流模型计算的圆柱入水过程圆柱运动轨迹和圆柱所受阻力时间曲线.可以看出，2种模型的数值模拟结果基本一致，所以入水过程中圆柱主要受气液两相流场压力分布不均引起的压差阻力，而其所受的摩擦阻力对圆柱入水过程受力和圆柱运动轨迹影响较小.

4 结束语

本文以Fluent软件为计算工具，应用VOF结合动网格技术的数值方法对水平圆柱入水过程气液两相流动和圆柱刚体运动问题进行了模拟，数值模拟的自由表面变化过程以及圆柱的刚体运动轨迹与经典文献的实验符合得很好.从中可以看出，本文应用的数值方法可以用来模拟物体入水特别是伴随着强非线性自由表面变化的问题，而之前常应用的边界元方法不能精确模拟此类问题;本文的数值方法可以应用来计算物体入水所受的冲击力，进而对物体如船体结构的设计提出指导意见和提供参考数据.

［1］王永虎，石秀华.入水冲击问题研究的现状与进展［J］.爆炸与冲击，2008，28(3):276-282.

WANG Yonghu，SHI Xiuhua.Review on research and development of water-entry impact problem［J］.Explosion and Shock Waves，2008，28(3):276-282.

［2］Von KARMAN T.The impact on seaplane floats during landing.NACA TN 321［R］.Washington:National Advisory Committee for Aeronautics，1929.

［3］WAGNER H.Uber stoss-und gleitvorgange an der oberflache von flussigkeiten［J］.Zeitschrift Für Angewandte Mathematik und Mechanik，1932，12(4):193-215.

［4］ZHAO R，FALTINSEN O M.Water-entry of two-dimensional bodies［J］.Journal of Fluid Mechanics，1993，246:593-612.

［5］ZHU Xinying，FALTINSEN O M，HU Changhong.Water entry and exit of a horizontal circular cylinder［J］.Journal of Offshore Mechanics and Arctic Engineering，2007，129:253-264.

［6］HIRT C W，NICHOLS B D.Volume of fluid(VOF)method for dynamics of free boundaries［J］.Journal of Computational Physics，1981，39:201-225.

［7］ARAI M，CHENG L Y，INOUE Y.A computing method for the analysis of water impact of arbitrary shaped bodies［J］.Journal of the Society of Naval Architects of Japan，1995，176:233-240.

［8］SCHUMANN C.Volume-of-fluid computations of water entry of bow sections［C］//Proceedings of Euromech 374.Poitiers，1998:209-217.

［9］XING-KAEDING Y，JENSEN G，PERIC M.Numerical simulation of water-entry and water-exit of a horizontal circular cylinder［C］//Proceedings of the 6th International Conference on Hydrodynamics.Perth，2004:663-669.

［10］GREENHOW M，LIN W M.Nonlinear free-surface effects:Experiments and theory.MIT report 83-19［R］.Cambridge:Massachusetts Institute of Technology，1983.

［11］陈震，肖熙.空气垫在平底结构入水砰击中作用的仿真分析［J］.上海交通大学学报，2005，39(5):670-673.

CHEN Zhen，XIAO Xi.Simulation analysis on the role of air cushion in the slamming of a flat-bottom structure［J］.Journal of Shanghai Jiao Tong University，2005，39(5):670-673.

［12］XING T，STERN F.Grid generation and post-processing for computational fluid dynamics(CFD)［Z］.［s.l.］:IIHR-Hydroscience and Engineering，2006.

［13］HADŽICA I，HENNIGB J，PERICM，et al.Computation of flow-induced motion of floating bodies［J］.Applied Mathematical Modelling，2005，29(12):1196-1210.