有限体积法的弹性结构动力学随机分析

陈卫东，陈浩，于艳春

(哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001)

舰船、潜艇等武器平台在战斗中不可避免地遭到离其数米甚至百米位置的爆炸冲击，这种爆炸通常不会使其产生严重的破损，但可能引起剧烈的振动，从而破坏武器上的机械设备和电子仪器，使其失去战斗力［1］.因此，研究远场爆炸载荷作用下结构的动力学随机响应问题具有重要的现实意义.

结构在随机载荷作用下的随机响应一直受到研究者的关注并不断取得进展.目前，求解随机响应问题的方法有Monte-Carlo法、随机有限元法和虚拟激励法等.Monte-Carlo法具有普遍的适用性，但其巨大的计算量限制了其在大型工程中的应用;随机有限元法虽然在静力学随机分析中得到广泛应用，但在动力学分析中发展缓慢［2］;而基于虚拟激励法的动力学随机响应分析主要应用在抗震、抗风等工程中［3-4］，对于爆炸等冲击载荷作用下随机动响应分析涉及较少.所以，文章将有限体积法与泰勒展开相结合，在考虑爆炸载荷的随机性时，求解了远场水下爆炸载荷作用下弹性结构动响应的统计特性，并对结构动响应的变异系数做了相关讨论.由于采用显式求解算法，同步求解结构动响应及其对基本随机变量的偏导，不需求解大型线性方程组，因而在计算爆炸冲击这一类问题时具有较高的效率.

1 有限体积法

有限体积法由于其思想简洁，用其导出的离散方程，物理上表示的是控制体积的通量平衡，方程中的各项有明确的物理意义，所以近来有不少学者将其应用于固体力学［5-6］.

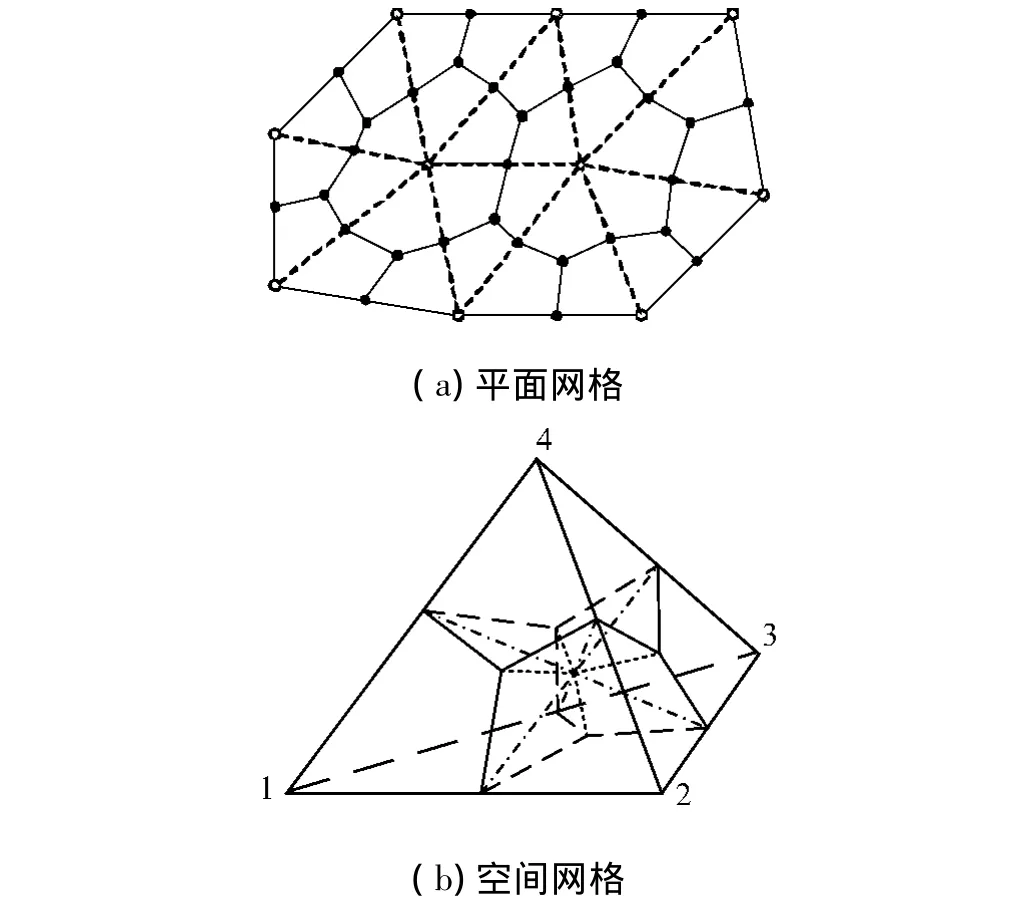
图1 控制体与其辅助网格示意Fig.1 Relation between control volume and auxiliary mesh

图1是非结构化网格示意图.对于图1(a)中平面网格:虚线网格为辅助网格(三角形)，连接辅助网格的重心及其各边中点(实心圆)就构成了控制体的边界，实线围成的闭合多边形即为控制体.显然，虚心圆即为辅助网格的节点，又为控制体的中心.对于三维问题，辅助网格为四面体，图1(b)给出了辅助网格与其内部控制体边界面的关系:每个四面体都被其内部控制体边界面分成体积相等的4部分.

在不考虑能量变化时，有限体积法的基本控制方程为动量守恒方程:

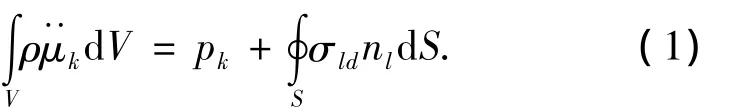
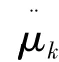
若将加速度、速度等变量定义在控制体中心，且辅助网格中应力、应变为常量，那么将式(1)在空间网格上离散，最终可得到求解三维弹性动力学问题的方程为［7］

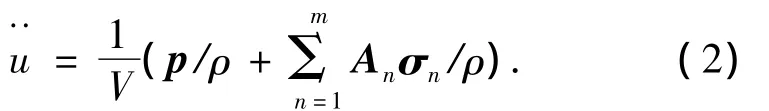
式中:m为控制体中心连接的四面体的个数.引入初始条件后，可采用文献［8］中的显式中心差分法求解式(2):

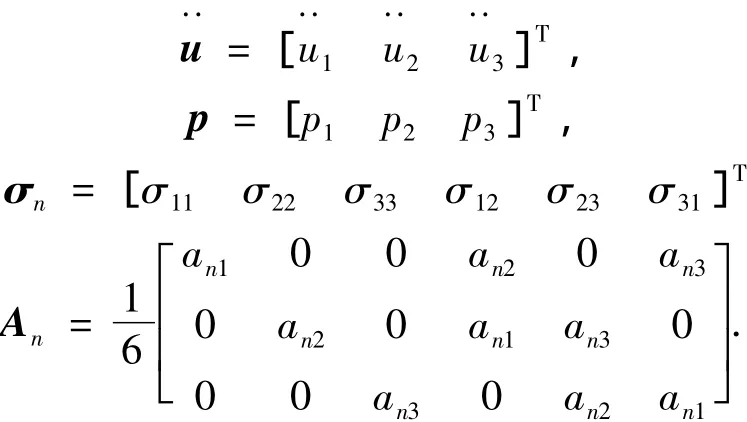
常数an1、an2和an3与控制体中心在四面体中的节点编号有关，若其在四面体节点编号中为1，则

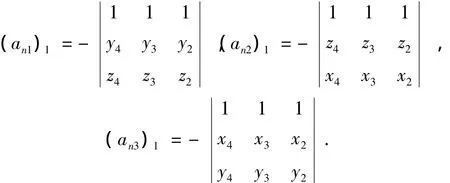
对其他的编号有同样形式的表达式，需要注意的是当前需求系数的节点编号与行列式中节点编号应符合右手定则:行列式中节点按逆时针排列，方向指向当前系数的节点编号.

2 结构动响应的统计特性

在不考虑结构尺寸的随机性时，设有一组基本随机变量X=(x1x2… xn)T，将式(2)对X求偏导得

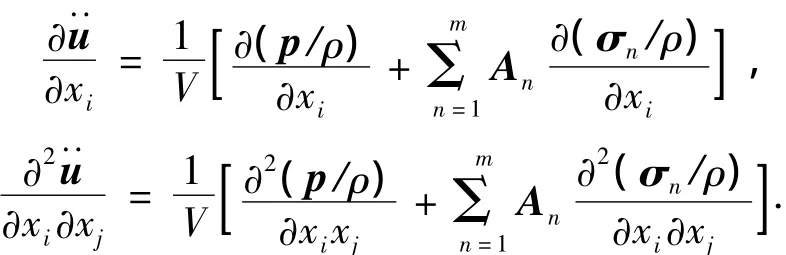
式中:i、j=1，2，…n.若 t时刻各物理量已知，则可利用显式算法得到t+Δt时刻的物理量对基本随机变量的偏导:

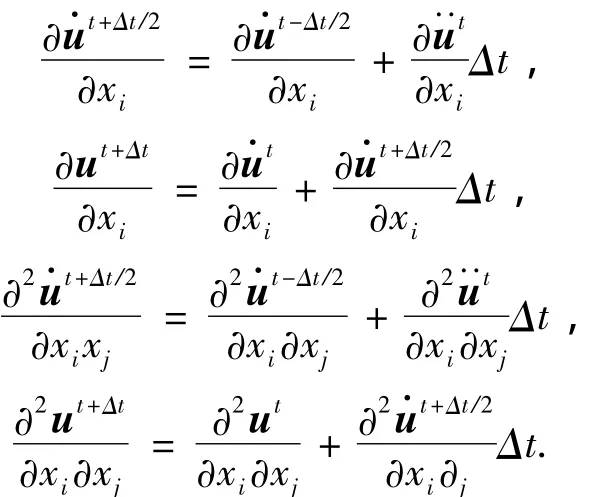
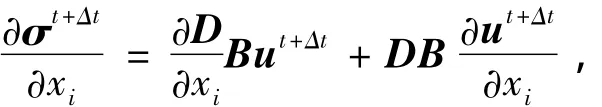
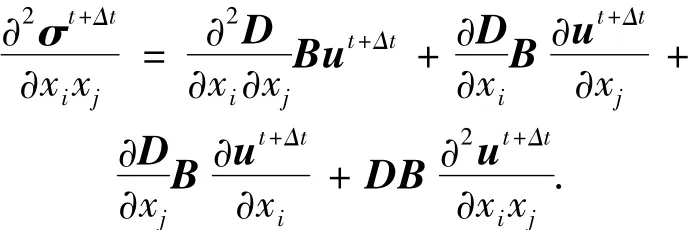
式中:D和B分别为弹性矩阵和几何矩阵，具体可参见文献［9］中有关常应力四面体元的表达式.

若要求解等效应力的统计特性，则还需要知道等效应力对基本随机变量的偏导.若skl为偏应力的分量，那么

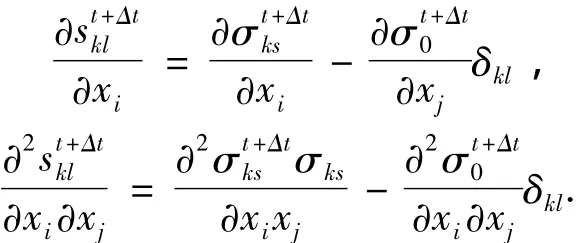
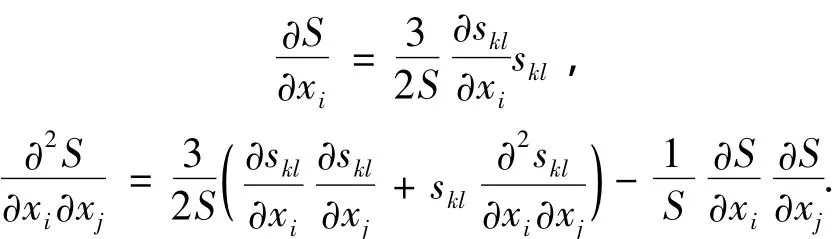
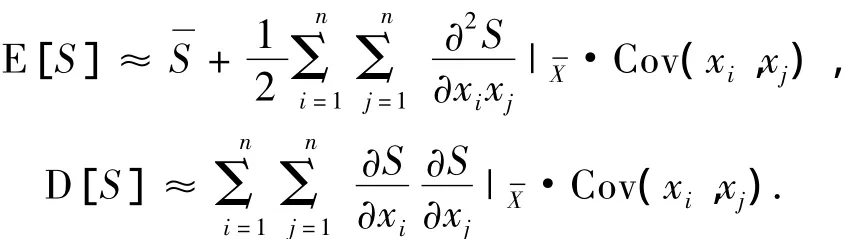
式中:Cov(xi，xj)为基本随机变量 xi和 xj的协方差，对于位移和应力的统计特征也是同样的方法.

3 固支板的随机动响应分析

为了验证前述理论的可行性，利用FORTRAN语言编写了计算程序，并计算了一个固支板遭受水下远场爆炸载荷的冲击问题.

3.1 爆炸载荷模型

水中冲击波过后压力随时间变化关系呈指数衰减规律:

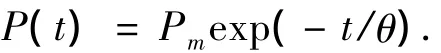
式中:Pm为冲击波超压峰值，θ为衰减时间常数.计算时，采用文献［10］中的经验公式:

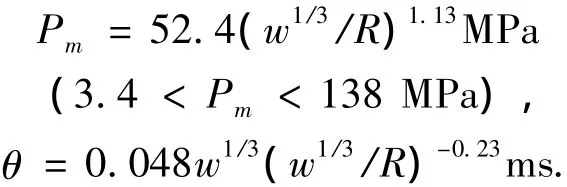
式中:w为TNT当量，kg;R为结构表面到爆源的距离，m.

对于远场爆炸，近似认为冲击波是平面压力波，并垂直作用于结构表面［11］.若忽略结构变形的影响，将冲击波看作是作用在刚体上，则作用于结构表面的压力p(t)与冲击波P(t)之间的关系为［12］

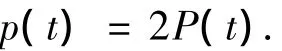
当把w和R作为基本随机变量时，该载荷模型就是一个随机爆炸载荷.

3.2 结构模型

计算模型见图2.材料密度ρ=7 800 kg/m3，弹性模量E=210 GPa，泊松比为0.3.将炸药的装药量w、板面到爆源的距离R看作相互独立的基本随机变量.由于结构在水中可能遭受各种炸药的爆炸冲击，为简化问题，将不同炸药都看成TNT，并对TNT的装药量和爆距取较大的变异系数来代表不同炸药性能的变异.各基本随机变量的取值见表1.

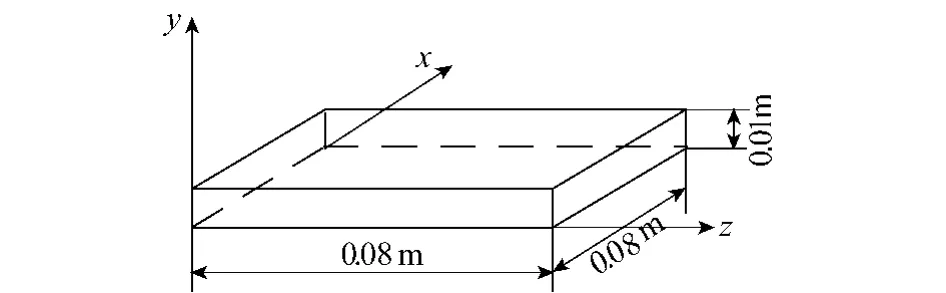
图2 固支板模型Fig.2 Model of a clamped plane

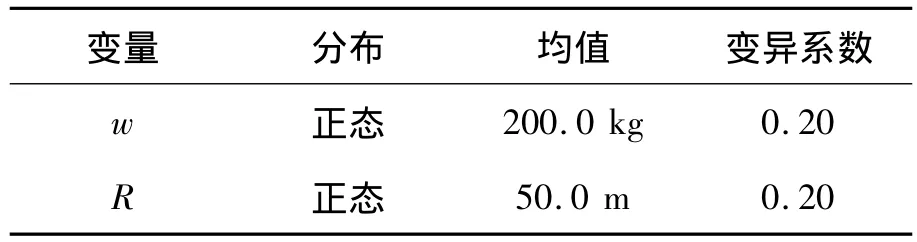
表1 基本随机变量统计特征Table 1 Statistical characterization of basic random variables

3.3 结构的随机动响应分析

利用前述的随机有限体积法(SFVM)计算了固支板在遭受爆炸载荷时动响应的统计特性:图3是板中心(0.04，0.01，0.04)处 y 向位移的均值和方差，图4 是点(0.04，0.01，0.00)处等效应力的均值和方差.

为验证计算结果的正确性，基于有限体积法进行了1 000组Monte-Carlo模拟.图3、4结果对比表明:SFVM与Monte-Carlo结果符合较好，该方法能准确的计算弹性结构动响应的统计特征.

图5(a)是板中心(0.04，0.01，0.04)处 y 向位移和点(0.02，0.01，0.02)处各向位移的变异系数绝对值;图5(b)是板中心点和点(0.04，0.01，0.00)处等效应力的变异系数.从图5可知，无论是节点位移变异系数的绝对值还是等效应力的变异系数，其随时间始终近似等于0.289 1.虽然当响应量的方差接近零时，变异系数有很大的波动，但这种波动只会使响应量的均值在接近于零时产生影响，并且当均值在零值附近时，其数量级与均值极值的数量级相差较大，所以可以忽略零值附近变异系数的波动，近似认为响应量的变异系数是不变的，因而可以推论:在弹性体内，当动载荷的随机性确定时，结构内各点动响应的变异系数绝对值是相同的，且不随时间发生变化.

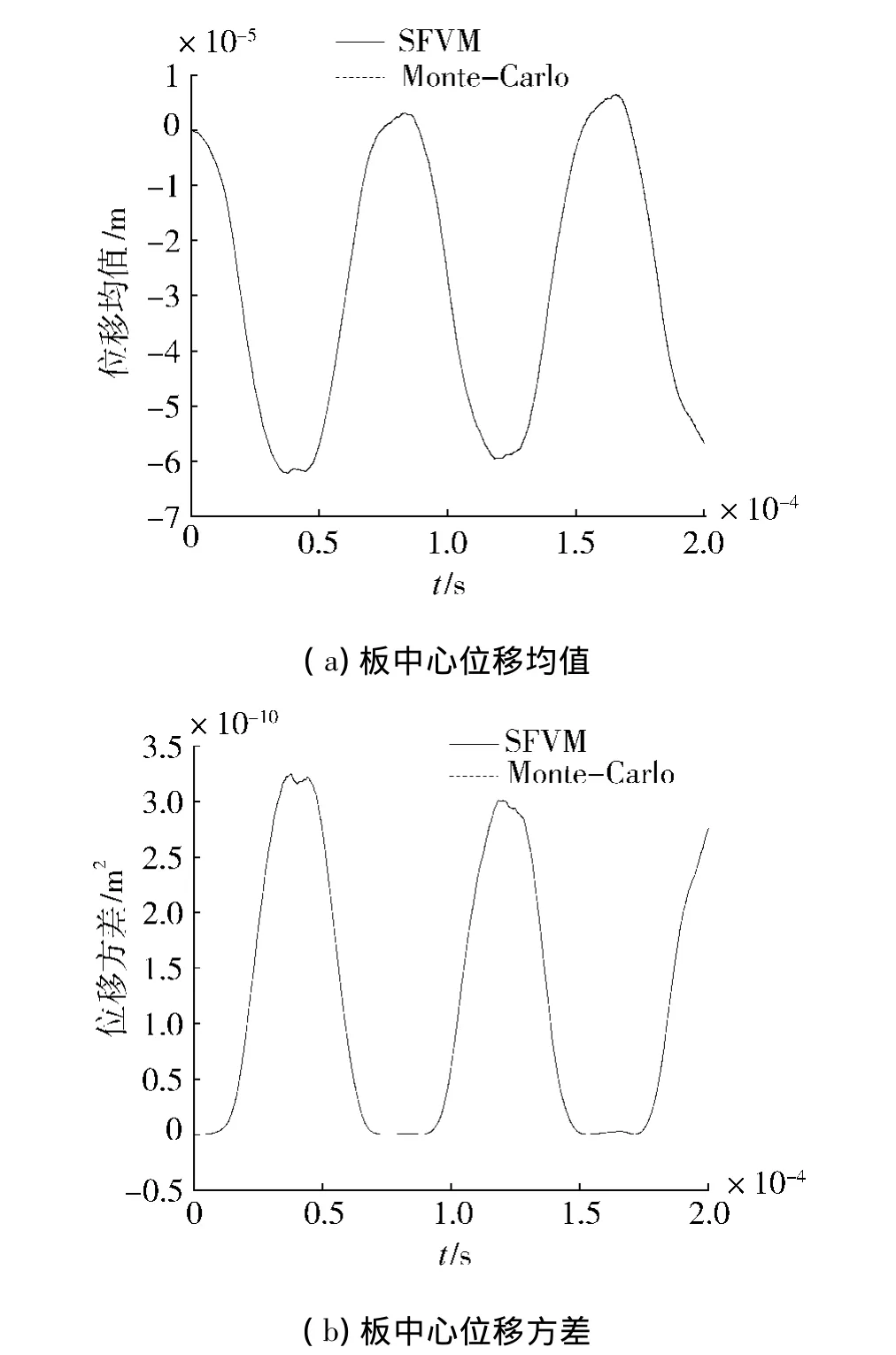
图3 板中心的位移统计特征Fig.3 Statistical characterization of central of the plane

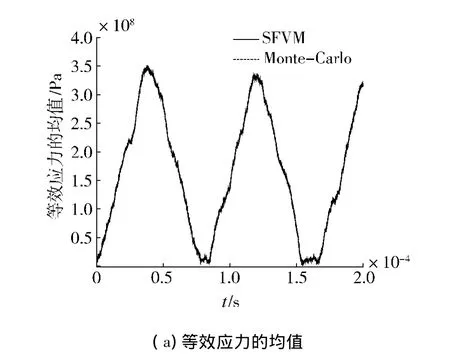
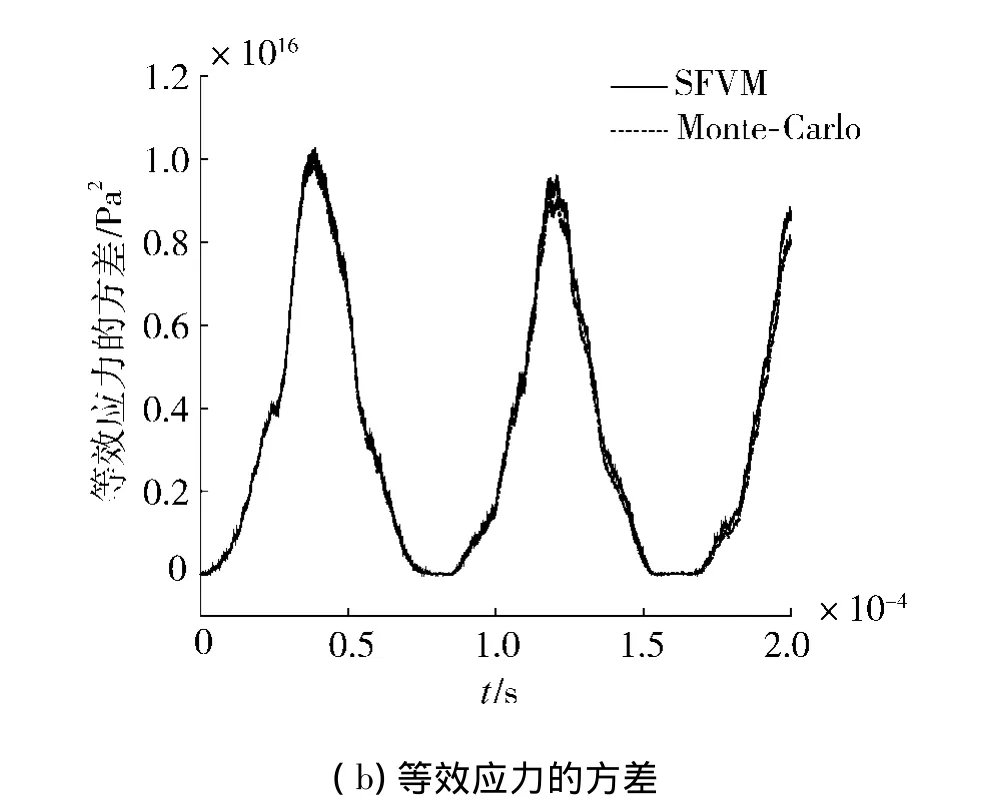
图4 等效应力的统计特征Fig.4 Statistical characterization of equivalent stress

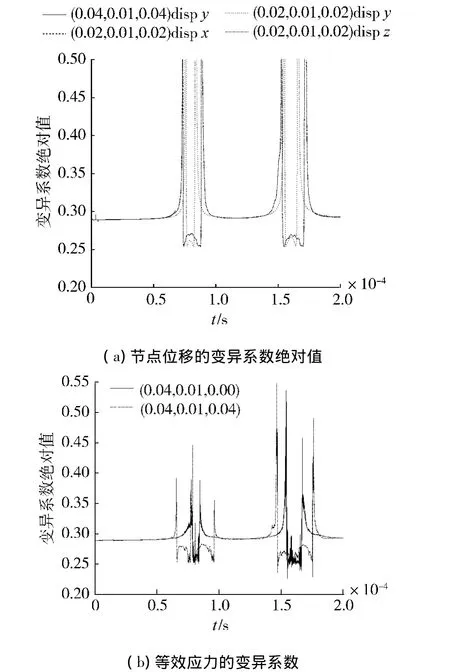
图5 响应量的变异系数Fig.5 Coefficient of variation for responses

为了证明以上推论的正确性，根据响应量的方差和变异系数 0.289 1，预测了点(0.04，0.01，0.02)处 y 向位移和点(0.02，0.01，0.00)处等效应力的均值，并与计算结果做了对比(图6)，结果表明该推论是可行的.利用该推论，只需计算响应量对基本随机变量的一阶偏导，因而提高了计算效率，为SFVM应用于大型工程提供了基础.

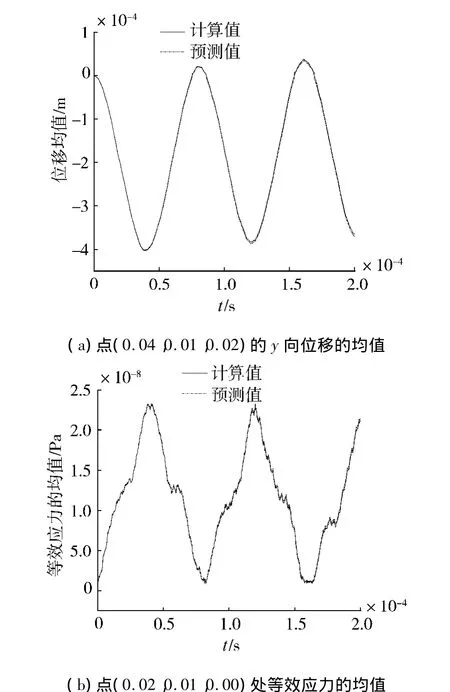
图6 响应量的均值预测Fig.6 Predicted mean value of responses

4 结束语

将有限体积法与泰勒展开结合，能够对任意随机载荷作用下弹性结构的动响应进行随机分析.而且在相同计算模型下，结构内各点动响应的变异系数绝对值近似相同，且不随时间发生变化.这样只要求出初始一段时间内响应量的变异系数和方差，就可以对响应量的均值进行预测，这使SFVM在具有较高精度的同时兼顾有较高的效率，为大型工程的动力学随机分析提供了一种途径.此外，由于对响应变异系数的讨论只限于文章中所给形式的随机爆炸载荷，所以文章中的推论不一定适用于其他形式的载荷，作者会在后续工作中继续讨论载荷形式和约束条件等对响应变异系数的影响.

［1］姚熊亮，郭君，许维军.船舶结构远场爆炸冲击动响应的数值试验方法［J］.中国造船，2006，47(2):24-34.

YAO Xiongliang，GUO Jun，XU Weijun.Far field numerical experimental method on the explosion impact dynamic responses of ship［J］.Ship Building of China，2006，47(2):24-34.

［2］安伟光，蔡荫林，陈卫东.随机结构系统可靠性分析与优化设计［M］.哈尔滨:哈尔滨工程大学出版社，2005:65-93.

AN Weiguang，CAI Yinlin，CHEN Weidong.Reliability analysis and optimal design of stochastic structural system［M］.Harbin:Harbin Engineering University Press，2005:65-93.

［3］LIN J H，ZHANG W S，WILLIAMS F W.Pseudo-excitation algorithm for non-stationary random seismic responses［J］.Eng Struct，1994，16(4):270-276.

［4］慕文品.受演变随机激励结构响应的扩展精细积分方法［J］.振动与冲击，2009，28(7):131-134.

MU Wenpin.An extended precise integration method for response of a structure subjected to evolutionary random exciation［J］.Journal of Vibration and Shock，2009，28(7):131-134.

［5］XIA Guohua，LIN Chinglong.An unstructured finite volume approach forstructuraldynamicsin responsetofluid motions［J］.Computers ＆ Structures，2008，86(7/8):684-701.

［6］LV X，ZHAO Y，HUANG X Y，XIA G H，SU X H.A matrix-free implicit unstructured multigrid finite volume method for simulating structural dynamics and fluid-structure interaction［J］.Journal of Computational Physics，2007，225:120-144.

［7］CHEN Weidong，CHEN Hao，ZHANG Wenping，et al.A finite volume method for 3-D elastodynamics［C］//Proceedings of the Third International Conference on Modeling and Simulation，VOL2-modelling and simulation in Engineering.Wuxi，China，2010:88-91.

［8］张雄，王天舒.计算动力学［M］.北京:清华大学出版社，2007:266-268.

［9］赵均海，汪梦甫.弹性力学及有限元［M］.2版.武汉:武汉理工大学出版社，2008:167-169.

［10］恽寿榕，赵衡阳.爆炸力学［M］.北京:国防工业出版社，2005:233-240.

［11］何建，肖玉凤，陈振勇，等.空爆载荷作用下固支矩形钢板的塑性极限变形［J］.哈尔滨工业大学学报，2007，39(2):310-313.

HE Jian，XIAO Yufeng，CHEN Zhenyong，et al.Plastic limited deformation analysis of the clamped rectangular steel plate subjected to air non-contact explosions［J］.Journal of Harbin Institute of Technology，2007，39(2):310-313.

［12］LIANG C C，TAI Y S.Shock responses of a surface ship subjected to noncontact underwater explosions［J］.Ocean Engineering，2006，33:748-772.