FRP增强混凝土缺口梁破坏模式的数值模拟
夏培秀,邹广平,唱忠良,唐立强
(哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001)
随着纤维增强复合材料(FRP)越来越多应用于诸如桥梁、房屋等这类混凝土构件的加固修复中,对FRP片材外贴与混凝土构件的受拉区以提高构件的强度,抑制裂缝扩展的研究也越来越受到国内外学者和工程技术人员的关注.由于混凝土本身抗拉强度低,受拉区容易出现裂缝,很多在役的混凝土构件都有裂缝的存在.随着裂缝的不断扩展,构件的承载力及其使用寿命将迅速下降.因此,对混凝土构件中裂缝的扩展机理及裂缝的加固补强技术进行研究有着重要的现实意义和应用价值.许多国内外学者都致力于FRP片材加固混凝土结构的研究,其研究的主要内容仍然集中于FRP片材加固混凝土在各种条件下的变形与强度,并且在试验中观察到了在不同的FRP片材加固参数下混凝土结构的承载能力及最终破裂形式.文献[1-4]对素混凝土及FRP片材加固的混凝土缺口梁进行了三点弯曲对比试验及数值模拟,探讨了2种梁的破坏机理及极限承载力,但对FRP片材加固混凝土结构在受力后裂纹萌生、扩展及其导致混凝土结构最终失效的机理研究方面,还有待于进一步研究.通过对FRP片材加固混凝土进行数值模拟,可从极限承载力和声发射信号方面入手来探讨FRP片材对混凝土梁的加固机理,进而深入研究FRP片材加固混凝土梁的裂缝形成机理及最终失效机理.
对纤维增强复合材料(FRP)加固混凝土缺口梁进行数值模拟时所采用的数值模拟方法系统考虑了混凝土材料性质的非均匀性,认为材料宏观破坏是细观单元破坏的积累过程.采用了Weibull分布来描述微元体的力学属性的离散性,当其应力状态满足最大拉应力准则或摩尔库仑准则时微元体开始破坏,破坏单元随变形的演化过程满足残余强度准则.通过弹性模量和强度等力学性质的弱化或退化描述单元的损伤[1-9].在准静态加载过程模拟中,外部载荷是分步施加的,借助于有限元进行应力分析,从而可以得到整个分析对象的应力和应变分布.
1 FRP片材加固混凝土构件的数值模型
按照文献[5]的实验模型建立混凝土及FRP片材的力学模型,如图1所示.
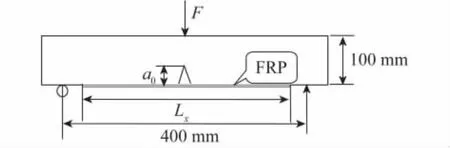
图1 计算模型Fig.1 Calculation model
混凝土简支梁长450 mm,截面尺寸100 mm×100 mm,FRP片材粘贴在梁下表面(受拉区).
混凝土和FRP片材的力学参数符合Weibull分布,在给定其均值度和平均值的条件下由程序进行随机赋值.混凝土计算所选用的力学参数:均质度为3,混凝土弹性模量为37.4 GPa,单轴抗压强度为146 MPa,泊松比为0.2,压拉强度比为10,残余强度系数为 0.1.FRP片材采用弹脆性模型,厚度为1 mm,均值度为 20,泊松比为 0.25,弹性模量为240 GPa,单轴抗拉强度为3 500 MPa,压拉强度比为3.为了考虑材料的拉伸破坏和剪切破坏特征,采用摩尔-库仑强度破坏准则,内摩擦角为30°.采用位移控制的分步加载方式.
参考国内外有关研究结果[6],如果选用强度高的环氧类粘贴胶并对混凝土贴面进行适当处理,增强后的混凝土三点弯曲梁界面附近的破坏通常并不是界面处粘贴层直接破坏,而是靠近界面处的混凝土破坏.因此,本文进行数值模拟时,假设FRP板与混凝土之间为完全固结,不设粘贴胶层.
2 数值模拟结果分析
2.1 极限承载力
表1给出了文献[5]中由试验所测得的极限承载力和由数值模拟所得到的极限承载力的结果.由表1可以看出,两者很相近,从而证明该数值模拟方法是可行的.从试件编号为Q01、Q02、Q11的数值模拟得到的极限载荷可知,随着缺口深度的增加,极限承载力减小.从试件编号为 Q02、Q03、Q05及 Q11、Q092 组的数值模拟结果可知,采用FRP片材外贴在混凝土梁的底部可提高混凝土梁的整体刚度和强度,从而提高其极限承载力.
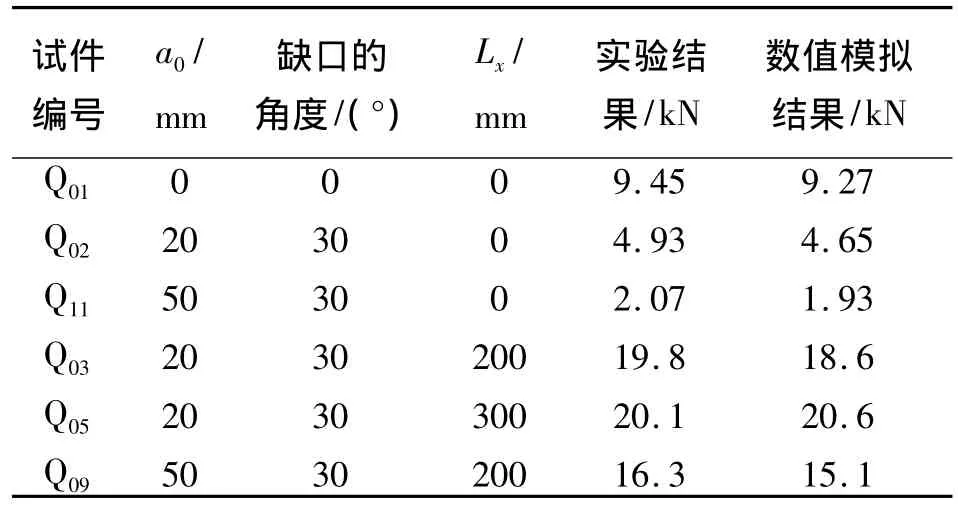
表1 试验和数值模拟所得到的极限承载力Table 1 Ultimate bearing capacity of experimental and numerical results
图2给出了缺口a0=20 mm,FRP片材的长度Lx=0、200、300 mm的载荷—位移曲线.由图2可知,贴了FRP片材的混凝土梁的极限承载力有明显的提高,而且曲线呈上升趋势.随着载荷的增加,混凝土局部开裂.当混凝土梁中出现大裂缝时,载荷—位移曲线上出现一个明显的台阶,大裂缝越多台阶也越多.可见,FRP片材的加固效果是明显的.
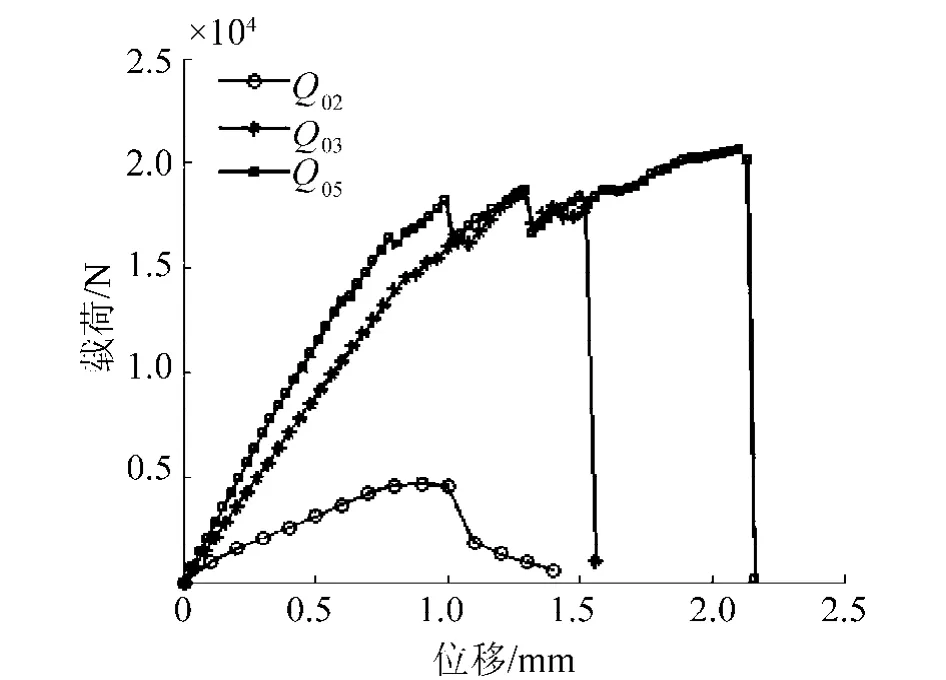
图2 载荷—位移曲线(a0=20 mm)Fig.2 Loading-displacement curves of specimens with 20 mm notches
材料变形、裂纹开裂及扩展过程都会产生声发射信号.在数值模拟中,混凝土单元的破坏就伴随着声发射信号的产生,声发射信号的次数是按破坏单元个数进行统计的.声发射信号的积累次数是统计到该步为止声发射信号的次数的总和.对于混凝土梁,在荷载作用下将产生损伤,进而发生失稳破坏,其宏观的破坏现象是许多微观破坏的综合表现,混凝土梁在整个变形过程中表现出突出的非线性.当梁中有微破裂产生时,载荷—位移曲线开始偏离线性,此后伴随着试件的变形,微破裂就不断产生,由此产生声发射信号,直到试件失稳破坏.图3给出了a0=20 mm,Lx=200、300 mm的混凝土梁的载荷及声发射信号与位移的关系.
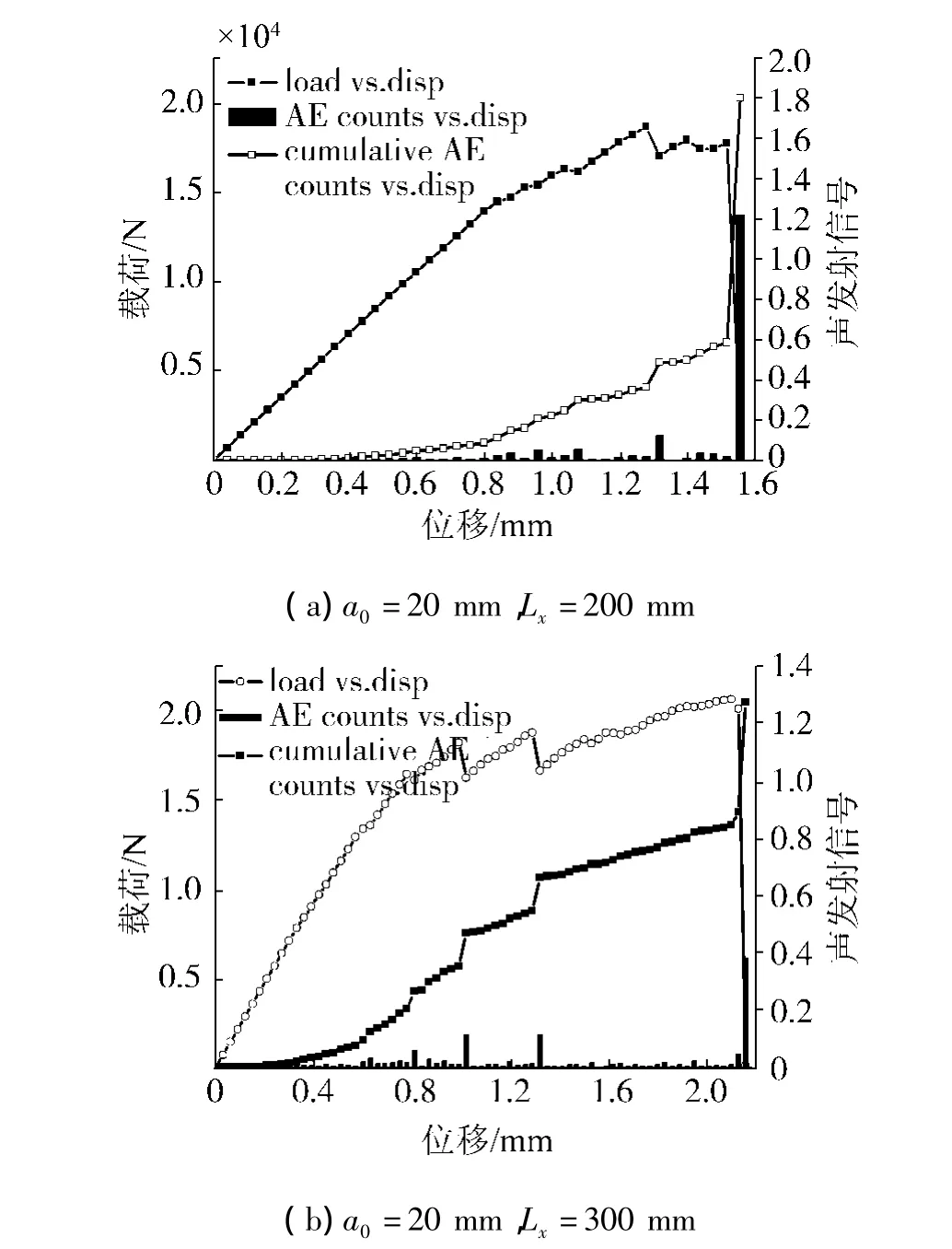
图3 混凝土梁的载荷及声发射信号与位移的关系Fig.3 Loading-displacement and loading-AE relationship of concrete beam
由图3可见:1)在加载的初始阶段基本没有声发射信号;2)随着载荷的继续增加,混凝土中出现破坏单元,并有声发射信号产生,当载荷达到最大值的80%左右时开始出现明显的声发射信号;3)当混凝土梁中产生裂缝时,载荷曲线上出现了明显的平台,此时声发射信号有明显的增加;4)当载荷达到极值,混凝土梁产生失稳破坏时,声发射信号剧增,释放出更多的能量.
2.2 破坏模式
图4给出了缺口深度为20 mm,FRP片材的粘贴长度分别为0、200、300 mm时混凝土梁破坏模式的数值模拟结果与文献[5]中的实验结果.从图4中可以看出,由数值模拟得到的混凝土梁的破坏模式与由实验获得的混凝土梁的破坏模式比较相似.进一步证明该数值模拟程序的可行性,为FRP片材增强混凝土梁的研究提供一种新的方法.
对于没有用FRP片材增强的混凝土梁(图4(a)),随着载荷的增加在缺口端部出现裂缝并迅速扩展,导致混凝土梁破坏,未出现其他宏观裂缝.破坏过程非常短暂,体现了脆性材料的破坏特点.
对于缺口深度为20 mm,FRP片材的粘贴长度为200 mm的混凝土梁(图4(b)),首先在缺口端部出现I型裂缝,该裂缝扩展到一定程度后停止扩展,而在FRP片材端部出现新的裂缝,最终由该裂缝的扩展导致混凝土梁破坏.FRP片材与混凝土之间并未剥离.
对于缺口深度为20 mm,FRP片材的粘贴长度为300 mm的混凝土梁(图4(c)),首先在缺口端部出现一条向上的宏观裂缝,扩展到一定程度后停止扩展,随着载荷的增加,靠近缺口根部界面处的混凝土出现一条斜裂缝,该裂缝扩展后与原有裂缝贯通,最后发展成通缝,导致混凝土失稳破坏.FRP片材与混凝土之间剥离.

图4 混凝土梁数值模拟结果与实验结果的对比Fig.4 Comparison of numerical simulation and experimental result of concrete beam
通过以上分析可知,对于FRP片材加固的混凝土梁,FRP片材的粘贴长度对混凝土梁的破坏模式有一定的影响.
2.3 破坏过程
图5、6给出了a0=20 mm,Lx=200 mm混凝土梁的破坏过程的最小主应力图.随着载荷的增加,试件在缺口端部出现一条向上的裂缝,即I型裂缝(见图5(a));载荷继续增加,该裂缝继续扩展(见图5(b));当该裂缝扩展至55 mm左右时,停止扩展,并在FRP片材的边缘出现一条向上的斜裂缝(见图5(c));该斜裂缝快速扩展,并发展为通缝,载荷值急剧下降,试件迅速破坏(见图5(d)).
进行数值模拟时规定压应力为正,所以最小主应力图反映了拉应力的分布特征[7].混凝土梁受力后,裂纹尖端拉应力集中,随着裂纹的扩展,拉应力也转移到新的裂纹尖端.这说明拉应力是促使裂纹扩展的主要驱动力.

图5 破坏过程的数值模拟Fig.5 Numerical simulation of failure process

图6 混凝土梁破坏过程的实验结果Fig.6 Experiment result of failure process of concrete beam
3 结论
1)本文对FRP片材加固混凝土梁进行了数值模拟,给出了载荷-位移曲线、声发射-位移曲线、混凝土梁的破坏模式,以及试件破坏过程中裂缝的扩展过程.
2)混凝土梁的极限承载力和破坏模式的数值模拟结果和实验结果较吻合.对比分析可知,FRP片材外贴在梁的底部对混凝土梁有明显的加固效果,并且FRP片材的粘贴长度对混凝土梁的破坏模式有一定的影响,进一步证明了文献[5]中的实验结果.
3)对混凝土梁在外载荷的作用下进行数值模拟时,单元的破坏伴随着能量的释放,产生声发射信号.当混凝土梁中产生裂缝时,释放出较多的能量,声发射信号会有明显的增加.并当混凝土发生破坏失稳时,声发射信号达到顶峰,混凝土梁释放出更多的能量.
4)采用本文的数值模拟方法对FRP片材加固的混凝土梁的破坏过程进行数值分析时,可以使人们更清楚地认识混凝土梁破坏过程的发生机理,为改善FRP片材加固的混凝土梁的力学性能提供力学依据.
[1]黄培彦,黄龙田,罗毅,等.纤维板增强钢筋砼缺口梁承载力试验研究[J].实验力学,2003,18(2):171-176.
HUANG Peiyan,HUANG Longtian,LUO Yi,et al.An experimental study on the load-carrying capacity of fibet-sheetreinforeed RC beam with a V-notch[J].Journal of Experimental Mechanics,2003,18(2):171-176.
[2]黄培彦,罗立峰,张桂森,等.碳纤维增强混凝土缺口梁承载力试验研究[J].实验力学,2001,16(3):250-255.
HUANG Peiyan,LUO Lifeng,ZHANG Guisen,et al.An experimental study on the load bearing capacity of carbon fibersheet-reinforced concrete 3-point bending specimen with a V-notch[J].Journal of Experimental Mechanics,2001,16(3):250-255.
[3]龙志勤,黄彦虎.碳纤维薄板粘贴长度对混凝土应力场的影响[J].茂名学院学报,2003,13(1):34-38.
LONG Zhiqin,HUANG Yanhu.Effects of the length of carbon fiber sheet on the stress field of concrete members[J].Journal of Maoming College,2003,13(1):34-38.
[4]孔德清,黄培彦.纤维增强混凝土缺口试件应力场数值分析[J].华南理工大学学报:自然科学版,2000,28(4):1-5.
KONG Deqing,HUANG Peiyan.Numerical analysis of the stress field on fiber-reinforced concrete fracture specimen with a V-notch[J].Journal of South China University of Technology:Natural Science Edition,2000,28(4):1-5.
[5]黄彦虎.碳纤维薄板增强砼缺口梁破坏机理及优化设计初探[D].广州:华南理工大学,2001:47-57.
HUANG Yanhu.Preliminary study on failure mechanism and optimal design of reinforced concrete notched beam with carbon fiber-sheet[D].Guangzhou:South China University of Technology,2001:47-57.
[6]汪长安,黄勇,孙哲峰,等.单向纤维布用于混凝土受弯构件的加固和修复[J].建筑材料学报,1999,2(2):171-175.
WANG Chang'an,HUANG Yong,SUN Zhefeng,et al .Strengthening and repairing concrete flexure beams by unidirectional carbon fiber sheets[J].Journal of Building Materials,1999,2(2):171-175.
[7]朱万成,王述红,唐春安.混凝土三点弯曲试验的计算机模[J].东北大学学报:自然科学版,1999,20(5):533-535.
ZHU Wancheng,WANG Shuhong,TANG Chun'an.Computer simulation on the three-point bending test of concrete Specimen[J].Journal of Northeastern University:Natural Science,1999,20(5):533-535.
[8]TANG C A,KOU S Q.Crack propagation and coalescence in brittle materials under compression[J].Engineering Fracture Mechanics,1998,61:311-324.
[9]LIU H Y,KOU S Q,LINDQVIST P A.Numerical simulation of the fracture process in cutting heterogeneous brittle material[J].International Journal for Numerical and Nanlytical Methods in Geomechanics,2002,26:1253-1278.

