M2-等可覆盖图的一个注记

张玉琴，姜雪娇

(天津大学理学院，天津 300072)

M2-等可覆盖图的一个注记

张玉琴，姜雪娇

(天津大学理学院，天津 300072)

图的覆盖问题是图论研究的一个主要内容.若图G的每个极小H-覆盖都是它的最小H-覆盖，则称图G为H-等可覆盖的.为刻画2M-等可覆盖图的特征，采用分类讨论的方法，得出2M-等可覆盖图的一个重要结果：若连通图G含6圈，则G不是2M-等可覆盖的.这为2M-等可覆盖图的完全刻画奠定了有力的基础.

H-覆盖；H-等可覆盖图；圈

图的覆盖问题是图论研究的一个主要内容,具有重要的理论意义与实际意义．H-等可覆盖图的刻画问题起源于对H-可分解图，随机H-可填充图及H-等可填充图见文献[1-8]的研究．文献[9]完全刻画了P3-等可覆盖图的特征，文献[10]刻画了一些特殊的M2-等可覆盖图．笔者考虑的图都是有限且没有孤立结点的简单图．图G的阶数为V(G)，边数为E(G).k个结点的圈用Ck表示．设M是边集E(G)的一个子集，如果M中任何2条边都不相邻，则称M是G的一个匹配.用Mt(t≥1)来表示t条边的匹配．设e∈E(G)，称G中与e不相邻的边数为e的边不邻度．

1 预备知识

首先给出文中需要的重要定义和已知结论．

定义1 设图H为图G的一个子图，H1,H2,…,Hk为同构于H的G的子图．若G的每条边至少出现在一个Hi(i=1,2,…,k )中，则{H1,H2,…,Hk}称为G的一个H-覆盖.

定义2 设H1,H2,…,Hk为G的一个H-覆盖.若对于任意Hj,j∈{1,2,…,k} ，)−E(Hj)都不是G的一个覆盖，则称{H1,H2,…,Hk}为G的一个极小覆盖．

定义3 若不存在少于k个同构于H的子图可覆盖G，则称{H1,H2,…,Hk}为G的最小H-覆盖．

定义4 若G的每个极小H-覆盖都是它的最小H-覆盖，则称G为H-等可覆盖的．

例如，圈C5是一个M2-等可覆盖图．文献[10]给出M2-等可覆盖图的以下结果．

命题1 含有m条边，最大度为d的图G，其最小2M-覆盖中所用2M数为

命题2 记e的边不邻度为d1(e)，N(e)表示边e的邻边集，c(G)表示G的最小M2-覆盖中所用的M2数，c0(e)表示N(e)的最小M2-覆盖中所用的M2数．若图G中存在边e，使得d1(e)+c0(e)＞c(G)，则G不是M2-等可覆盖的；若图G中存在边e，使得d1(e)+c0(e)=c(G)．且e的邻边集N(e)中有2条边与G−N(e)中某同一条边不相邻，则G不是M2-等可覆盖的．

2 主要结果

给出如下2个重要命题．

命题3 非M2-可覆盖图可划分为3类：

(1) G中仅存在1条边e与其余边均相邻，G−e是M2-可覆盖的；

(2) G中恰存在2条相邻边ei和ej分别与其余边均相邻，G−ei−ej是M2-可覆盖的；

(3) G中至少存在3条边与其余边均相邻，即G为星K1,k(k≥3)或K3.

证 明 由可覆盖图的定义立刻可得.

显然，若G不是M2-可覆盖的，G一定不是M2-等可覆盖的．

命题4 设图F为图G的一个M2-可覆盖子图，若F不是M2-等可覆盖的，且G−F是M2-可覆盖的，则图G不是M2-等可覆盖的.

证 明 取F的一个不是最小覆盖的极小M2-覆盖，再任取G−F的一个M2-覆盖，它们的并显然是G的一个非最小覆盖的极小M2-覆盖，由等可覆盖的定义知，图G不是M2-等可覆盖的.

定理1 若连通图G含6圈，则G不是M2-等可覆盖的.

证 明 因对C6的每条边e，都有d1(e)=3，c0(e)=1，c(C6)=3，d1(e)+c0(e)＞c(C6).由命题2，圈C6不是M2-等可覆盖的.

情形1 GC−中仅存在一条边e与其余边均相邻，即GCe−−是2M-可覆盖的.因为e至多与C的4条边相邻，即至少有C的2条边与e不相邻，不妨设其中的一条边为e1.则{{e1,e}，{e1,e3}，{e1,e4}，{e2,e5}，{e2,e6}}是C∪e的一个极小M2-覆盖，因为， C∪e的最小M2-覆盖中所用M2数为4，所以它不是C∪e的最小M2-覆盖，从而C∪e不是M2-等可覆盖的，而G−C−e是M2-可覆盖的，由命题4，G不是M2-等可覆盖的．

情形2 G−C中恰存在2条边ei和ej分别与其余边均相邻，即G−C−ei−ej是M2-可覆盖的．因为ei与ej必相邻，对于C∪ei∪ej，有以下2种可能．

(1) C中至少存在1条边(不妨设为e1)与ei和ej均不相邻，则{{e1,ei}，{e1,ej}，{e1,e3}，{e1,e4}，{e2,e5}，{e2,e6}}是C∪ei∪ej的一个不是最小覆盖的极小M2-覆盖，故C∪ei∪ej不是M2-等可覆盖的，因而G不是M2-等可覆盖的．

(2) C中每条边都至少与ei和ej之一相邻．只有图1所示一种可能．

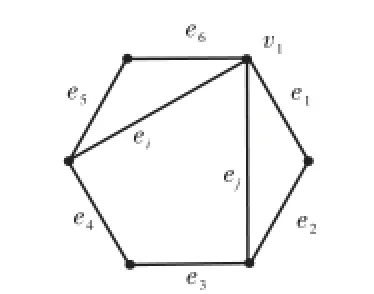
图1 情形2(2)示意Fig.1 Illustration of case 2(2)

图1中{{e2,ei}，{e4,ej}，{e1,e3}，{e2,e5}，{e2,e6}}是C∪ei∪ej的一个不是最小覆盖的极小M2-覆盖，故C∪ei∪ej不是M2-等可覆盖的，因而G不是M2-等可覆盖的．

情形 3 G−C为K3因G是连通的，有以下3种可能．

(1) C与K3有1个公共结点，则{{e2,ei}，{e4,ej}，{e4,ek}，{e1,e3}，{e2,e5}，{e2,e6}}是图C∪K3(即图G)的一个不是最小覆盖的极小M2-覆盖，所以G不是M2-等可覆盖的．

图2 情形3(1)示意Fig.2 Illustration of case 3(1)

(2) C与3K有2个公共结点，有图3所示3种可能．

图3 情形3(2)示意Fig.3 Illustration of case 3(2)

图3(a)中，{{e2,ei}，{e4,ej}，{e4,e1}，{e1,e3}，{e2,e5}，{e2,e6}}是图G的一个不是最小覆盖的极小M2-覆盖.

图3(b)中，{{e2,ei}，{e4,ej}，{e1,e3}，{e2,e5}，{e2,e6}，{e4,ek}}是图G的一个不是最小覆盖的极小M2-覆盖．

图3(c)中，{{e2,ei}，{e4,ej}，{e1,e3}，{e2,e5}，{e2,e6}，{e4,ek}}是图G的一个不是最小覆盖的极小M2-覆盖.

所以G不是M2-等可覆盖的．

(3) C与K3有3个公共结点，只有图4所示1种可能．

图4 情形3(3)示意Fig.4 Illustration of case 3(3)

则{{e1,e5}，{e2,ei}， {e3,e5}，{ej,e5}，{e4,e6}，{ek,e6}}是图C∪K3(即图G)的一个不是最小覆盖极小M2-覆盖.

情形4 G−C为星K1,k(k≥3).记星K1,k(k≥3)的k条边分别为e01,e02,…,e0k.因为G是连通的，有2种可能．

(1) 星的中心是C的一个结点(不妨设为v1).又有如下4种可能：

① 星的其余结点均不在C上.则{{e2,e01}，{e2,e02}，…，{e2,e0k}，{e1,e3}，{e1,e4}，{e2,e5}，{e2,e6}}是图G的一个不是最小覆盖的极小M2-覆盖(见图5).

图5 情形4(1)①示意Fig.5 Illustration of case 4(1)①

② 星的其余结点只有1个结点v0i在C上，不妨设v1v0i=e0i.有图6所示2种可能．

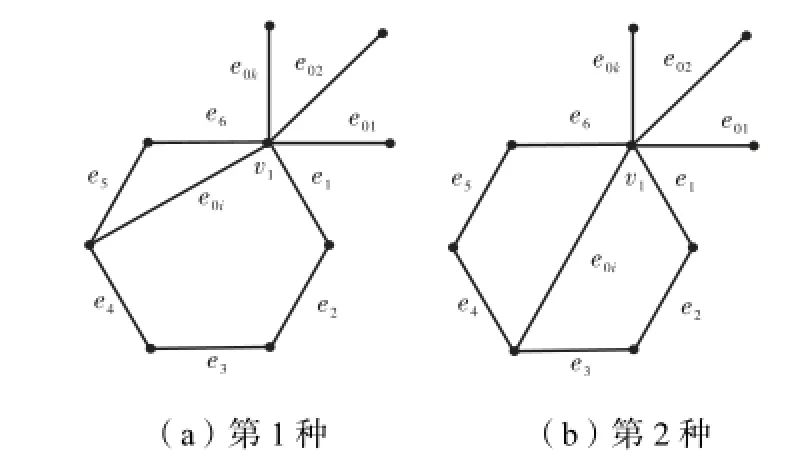
图6 情形4(1)②示意Fig.6 Illustration of case 4(1)②

无论哪个图中，{{e2,e01}，{e2,e02}，…，{e2,e0i}，…，{e2,e0k}，{e1,e3}，{e1,e4}，{e2,e5}，{e2,e6}} 都是图G的一个不是最小覆盖的极小M2-覆盖.

③ 星的其余结点中恰有2个结点v0i，v0j在C上，不妨设v1v0i=e0i，v1v0j=e0j，有图7所示2种可能．

图7 情形4(1)③示意Fig.7 Illustration of case 4(1)③

图7(a)中，{{e2,e01}，{e2,e02}，…，{e2,e0i}，…，{e2,e0k}，{e1,e3}，{e1,e4}，{e2,e5}，{e2,e6}}是图G的一个非最小覆盖的极小M2-覆盖.

图7(b)中，{{e3,e01}，{e3,e02}，…，{e3,e0i−1}，{e4,ei}，{e3,e0i+1}，…，{e3,e0k}，{e5,e3}，{e6,e3}，{e1,e4}，{e2,e4}}是图G的一个非最小覆盖的极小M2-覆盖.

④ 星的其余结点恰有3个在C上.只有图8所示1种可能．

图8 情形4(1) ④示意Fig.8 Illustration of case 4(1)④

这时，存在边e3，使得d1(e3)=k+6−4−1=k +1，c0(e3)=2，c(G)=k+2，d1(e3)+c0(e3)＞c(G)，由命题2，G不是M2-等可覆盖的.

所以，在(1)下，G都不是M2-等可覆盖的.

(2) 星的中心在C的结点外.因为G是连通的，有6种可能.

① 星的其余结点中只有1个结点在C上，如图9所示．

图9 情形4(2)①示意Fig.9 Illustration of case 4(2)①

则存在边e2，使得d1(e2)=k+6−3=k+3，

② 星的其余结点中恰有2个结点在C上，有图10所示3种可能．

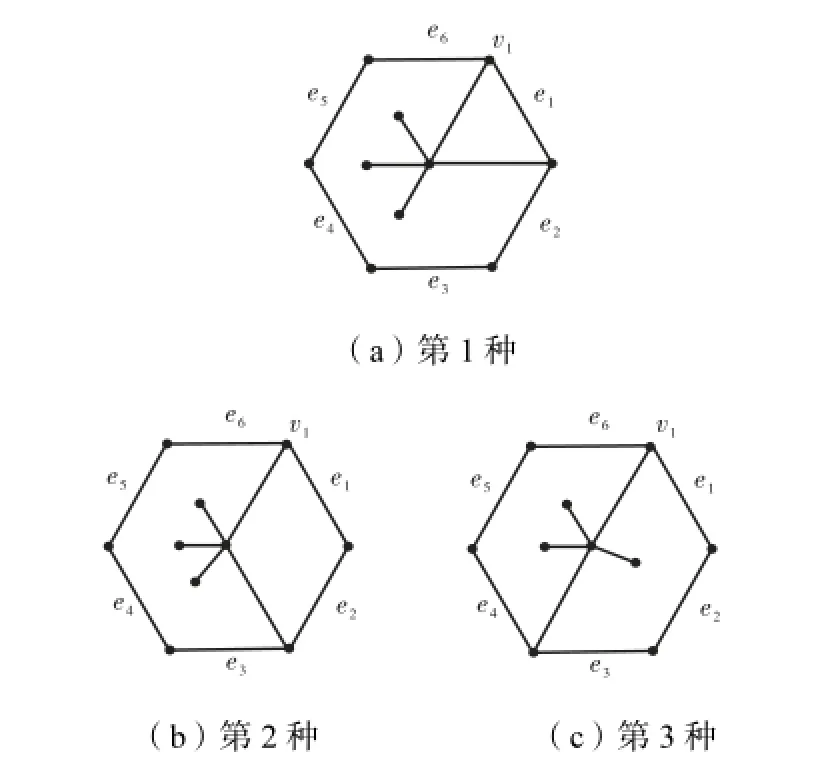
图10 情形4(2)②示意Fig.10 Illustration of case 4(2)②

图10中都存在边e5，使得d1(e5)=k+6−3=

③ 星的其余结点中恰有3个结点在C上，有图11所示3种可能．

在图11(a)(b)中，存在边e5，d1(e5)=k+6−3=边e2，d1(e2)=k+6−3−1=k+2，c0(e2)=2,Δ(G) =k，

④ 星的其余结点中恰有4个结点在C上，有图12所示3种可能．

图11 情形4(2)③示意Fig.11 Illustration of case 4(2)③

图12 情形4(2)④示意Fig.12 Illustration of case 4(2)④

都存在边5e，使得

⑤ 星的其余结点中恰有5个结点在C上，只有图13所示1种可能．

则存在边e5，使得d1(e5)=k+6−3−1=k+2，

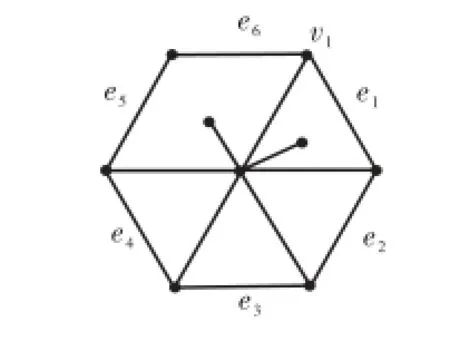
图13 情形4(2)⑤示意Fig.13 Illustration of case 4(2)⑤

⑥ 星的其余结点中恰有6个结点在C上，只有图14所示1种可能．

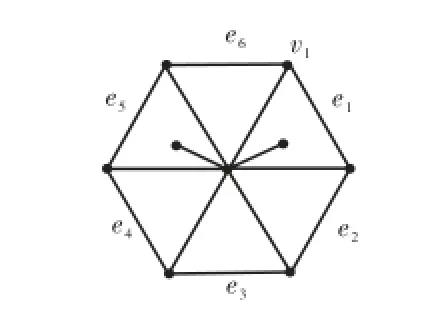
图14 情形4(2)⑥示意Fig.14 Illustration of case 4(2)⑥

则对边e5，有d1(e5)=k+6−4−1=k+1，c0(e5)=

所以，在情形4的(2)下，由命题2，G都不是M2-等可覆盖的．

综上，若G含6圈，则G不是M2-等可覆盖的．

类似可得：

定理2 若连通图G含7圈，则G不是2M-等可覆盖的.

3 结 语

定理1和定理2的得出，为2-M等可覆盖图的完全刻画奠定了有力的基础.

［1］ Ruiz S. Randomly decomposable graphs[J]. Discrete Mathematics，1985，57(1/2)：123-128.

［2］ Beineke L W，Hamberger P，Goddard W D. Random packings of graphs[J]. Discrete Mathematics，1994，125 (1/2/3)：45-54.

［3］ Hartnell B L，Vestergaard P D. Equipackable graphs[J]. Bull Inst Combin Apl，2006，46：35-48.

［4］ Vestergaard P D. A short update on equipackable graphs [J]. Discrete Mathematics，2008，308(2/3)：161-165.

［5］ Zhang Yuqin，Fan Yonghui.2M-equipackable graphs[J]. Discrete Applied Mathematics，2006，154(12)：1766-1770.

［6］ Zhang Yuqin.3P-equicoverable graphs：Reasearch on H-equicoverable graphs[J]. Discrete Applied Mathematics，2008，156(5)：647-661.

［7］ Molina R，McNally M，Smith K. Characterizing randomly Pk-decomposable graph for k≤9[J]. Congressus Numerantium，2002，156：211-221.

［8］ Bialostocki A，Roditty Y. 3K2-docomposition of a graph [J]. Acta Math Hunger，1982，40：201-208.

［9］ Zhang Yuqin. P3-equicoverable graphs：Reasearch on H-equicoverable graphs[J]. Discrete Applied Mathematics，2008，156(5)：647-661.

［10］ 张玉琴，兰文华. 几类特殊的M2-等可覆盖图[J]. 天津大学学报，2009，42(1)：83-85.

Zhang Yuqin，Lan Wenhua. Some special2-Mequicoverable graphs[J]. Journal of Tianjin University，2009，42(1)：83-85(in Chinese).

Note on M2-Equicoverable Graphs

ZHANG Yu-qin，JIANG Xue-jiao
(School of Sciences，Tianjin University，Tianjin 300072，China)

Covering of graphs is a main content of graph theory. A graph G is called H-equicoverable if every minimal H-covering in G is also a minimum H-covering in G. To give the characterization of M2-equicoverable graphs，an important result for connected M2-equicoverable graphs is obtained by using the method of case by case：if Gis a connected graph that contains a 6-cycle，then G is not M2-equicoverable. This result provides a strong base for entirely characterizing all M2-equicoverable graphs.

H-covering；H-equicoverable graph；cycle

O157.5

A

0493-2137(2011)05-0466-05

2010-03-01；

2010-06-04.

国家自然科学基金资助项目（10926071，10701033）.

张玉琴（1974— ），女，博士，副教授.

张玉琴，yuqinzhang@126.com.