爆炸载荷作用下单向加筋方板的大挠度塑性动力响应分析

刘敬喜，刘 尧，汤皓泉，李 威

(1.华中科技大学 船舶与海洋工程学院，武汉 430074;2.中国舰船研究设计中心，武汉 430064)

爆炸载荷作用下结构的非弹性动力响应是十分复杂的。早期的研究绝大多数都是关于梁、板等简单结构的非线性动力响应问题，对于工程中广泛应用的加筋板结构的研究，主要是通过实验及数值模拟的手段研究其塑性动力响应［1－6］。采用理论方法研究加筋板结构的塑性动力响应方面，目前主要还是采用刚塑性简化模型。1993年，Schubak等［7］采用刚塑性梁模型对爆炸载荷作用下的加筋板结构作了较为系统的理论研究。1994年，刘土光和唐文勇等［8－10］采用虚功原理讨论了“十字形”加筋固支方板以及矩形加筋板的刚塑性动力响应。1995年，吴有生等［11］采用能量法推导了一个计算爆炸载荷作用下舰船板架塑性变形及破损的公式，并与有关实验进行了比较。最近，方斌等［12］采用能量法讨论了水下爆炸冲击波荷载作用下船底板架的塑性动力响应。

实验研究以及理论分析结果表明［4，13］:取决于加强筋的相对刚度以及爆炸载荷峰值的大小，加筋板的变形模式将呈现3种不同的形式:① 当加强筋的相对刚度较小时，加筋板面板传递给加强筋的动反力使加强筋迅速进入机构状态，从而加筋板面板和加强筋将作为一个整体一起发生运动;② 当加强筋的相对刚度足够大时，加筋板面板传递给加强筋的动反力不足以使加强筋进入机构状态。从而在整个冲击过程中，加强筋始终处于近似刚性状态，加强筋之间的板格将以加强筋为固定边界发生运动;③ 对于加强筋的相对刚度不太大的情况，当爆炸载荷的峰值导致板格进入机构状态运动后，由板格传递给加强筋的动反力同时使加强筋亦进入机构状态。在此情况下，将发生板格的局部变形与加筋板总体变形耦合运动的状况。

就船舶加筋板结构而言，其加强筋的相对刚度一般较小。故爆炸载荷作用下船舶加筋板的变形模式大多归属于第1种变形模式，即所谓加筋板的总体变形模式。基于上述理由，本文将限于第1种变形模式的讨论，从分别列出加筋板面板以及加强筋的运动方程出发［13］，详细分析了爆炸载荷作用下单向加筋固支方板的大挠度塑性动力响应。首先讨论了同时计及弯矩和面力(轴力)作用的解析解，在此基础上进一步讨论了忽略弯矩影响的薄膜解，给出了爆炸载荷作用下加筋板永久变形的计算式。本文还参照文献［14］和［15］给出的简化能量解法，导出了爆炸载荷作用下加筋板永久变形的计算式。

计算实例采用文献［3］给出的单向加筋固支方板的实验模型。理论结果与文献［3］的实验结果比较表明，在多数情况下符合良好。

1 爆炸载荷作用下单向加筋板的理论分析模型

1.1 单根加强筋固支方板

讨论图1(a)所示的具有单根加强筋的固支方板，板的边长为2a，厚度为h，矩形截面加强筋的宽度为b1，高度为h1，其上承受均布爆炸载荷q(t)的作用。假定加筋板的材料是理想刚塑性的，因此不计材料的弹性以及应变强化的影响。

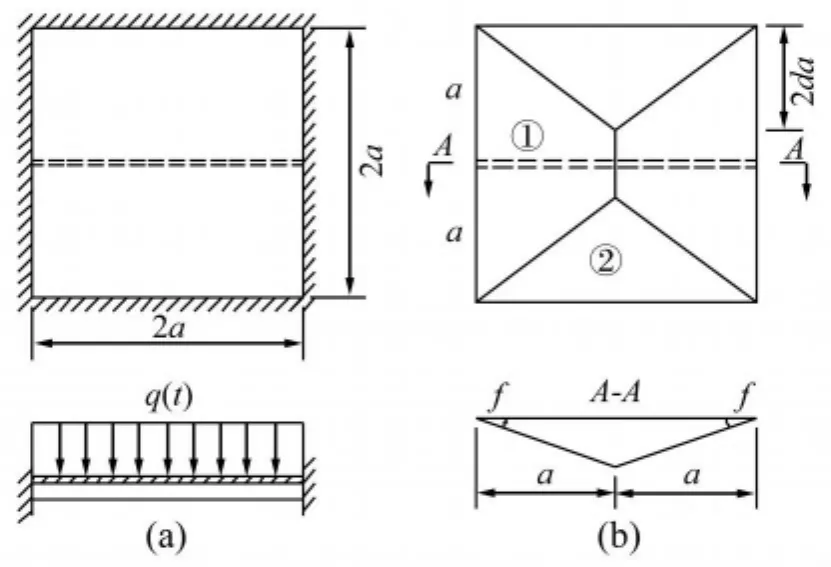
图1 单根加筋固支方板Fig.1 Built-in square plates with single stiffener

限于讨论单根加筋固支方板的总体变形模式。在此情况下，加筋板的面板和加强筋作为一个整体发生运动，如图1(b)所示。

假定爆炸载荷作用下单向加筋固支方板的总体变形模式与其静载作用下的静力总体破坏模式具有相同的形式。因此，首先应从讨论加筋板的静力平衡着手确定单根加筋固支方板的总体破坏模式。

列出刚性板块①和②的静力平衡方程，最后得到:

式中，q0为加筋板的静力极限载荷值;M0=σyh2/4，为加筋方板面板的极限弯矩;σy为材料的屈服应力;M'0=σy/4，为加强筋的极限弯矩;δ为表征塑性铰线位置的无因次参数。

联立求解(3)、(4)两式，最后得:

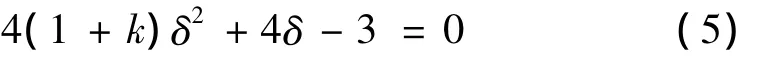
已知加强筋的相对刚度k，则可由上式求出确定塑性铰线位置的δ值，再将δ值代入式(4)，便得到单根加筋固支方板的静力极限载荷值。因此，当爆炸载荷的初始峰值时，固支加筋方板便开始发生运动。

进一步讨论爆炸载荷作用下单根加筋固支方板的大挠度塑性动力响应。加筋板刚性板块①的运动方程为:

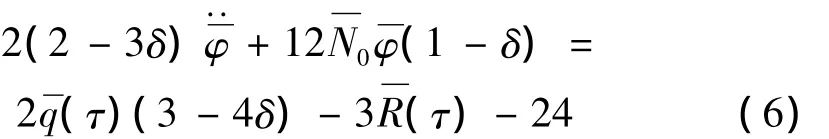
加强筋的运动方程为:

给出q(τ)的具体形式后，就不难求得上述运动方程的解。

1.2 双加强筋固支方板

以上讨论了爆炸载荷作用下单根加筋固支方板的大挠度塑性动力响应。上述分析方法可以推广至具有2根或2根以上加强筋的固支方板的情况。对于具有双加强筋的固支方板(图2)，参照上一小节的讨论，首先确定它的静力总体破坏模式。与单根加筋的情况相类似，已知加强筋的相对刚度，便可由下式确定塑性铰线的位置:

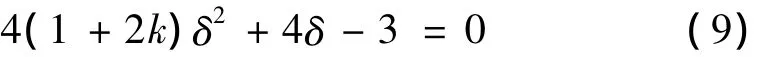
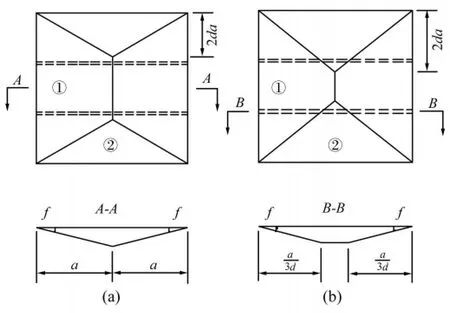
图2 双根加筋固支方板Fig.2 Built-in square plates with double stiffener

进一步讨论爆炸载荷作用下双根加筋固支方板的大挠度塑性动力响应。首先讨论倾斜塑性铰线未越过加强筋时的情形，如图2(a)所示。加筋板刚性板块①以及加强筋的运动方程分别为:

联立求解(10)、(11)两式，消去R(τ)得:

加筋板刚性板块①以及加强筋的运动方程分别为:

联立求解(13)、(14)两式，消去R(τ)得:

求出q(τ)的具体形式后，就不难求得上述运动方程的解。

2 爆炸载荷作用下单向加筋板的能量解

限于讨论固支加筋方板总体破坏模式的情形。与上一小节的解析解有所不同，固支加筋方板的挠曲面改取为二次曲面的形式［15］，如图3所示。

式中w0表示固支加筋方板中央的永久变形值。

图3 固支加筋方板的总体变形模式(能量解)Fig.3 The global deformation mode of build-in stiffened square plate(energy solution)

在大变形的情况下，膜力在板的塑性动力响应中起到了主要的作用，从而可以忽略弯矩的影响［13－15］。为了计及应变率效应的影响，将平均动屈服应力σd表示为静屈服应力σy乘于某一大于1的系数。即有:

由(16)式，对应的应变表达式为:

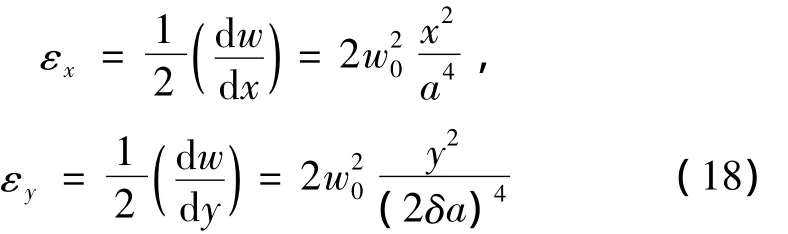
固支加筋方板在变形过程中所做的塑性功为:

式中，F为加强筋的横截面面积。

固支加筋方板所承受的初始动能为:

式中，ρ为加筋板材料的密度;I为爆炸载荷传递的总冲量，这里假定爆炸载荷沿加筋方板表面是均匀分布的。

根据能量原理，应有:

将(19)、(20)两式代入上式，经整理后得到:

参照文献［15］中的论述，在本文的计算中取α=2.80。

对于具有双加强筋的固支方板，板的最大永久变形的计算式仍具有式(22)的形式，只需将Φ的计算式改写为以下形式:

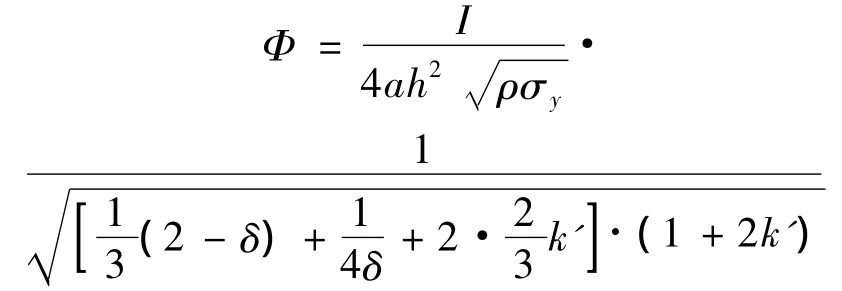
3 算例

为了验证本文提出的计算方法的合理性，计算实例采用文献［3］给出的单向加筋固支方板的实验模型。加筋方板的边长为126mm×126mm，板厚为1.6mm;加强筋为矩形截面梁，其宽度和高度的名义尺寸分别为3mm×3mm和3mm×7mm，加筋方板面板的厚度以及加强筋截面的实际尺寸列于表1中。单筋和双筋的布置方式采用等分以及三等分方板的形式。其中单根加筋的实验模型共6个，双筋模型共2个。

加筋板的材料为软钢，材料的静屈服应力为σy=242 MPa。计算中取平均动态屈服应力 σd=2.8σy，即α =2.8。

在文献［3］中，爆炸载荷取矩形脉冲的形式。载荷的持续时间T=14.5 μs，已知爆炸载荷的总冲量值 I，便可计算出分布爆炸载荷值其中 A=4a2，为实验模型的面积。将它表示成无因次的形式:

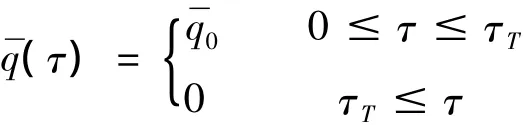
对于矩形脉冲载荷的情况，单根加筋固支方板运动方程(8)的求解将得到很大的简化。在此情况下，加筋板的塑性动力响应分为两个运动阶段。

首先讨论加筋板运动的第一阶段(0≤τ≤τT)。此时，常数，微分方程(8)成为一个线性常微分方程。当满足初始条件τ=0时，，解得:

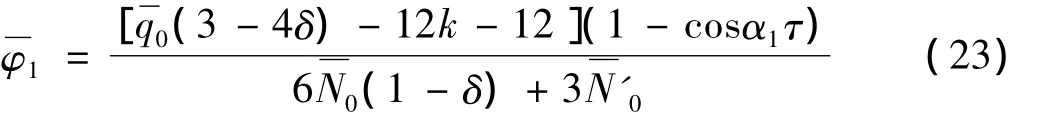
其次讨论加筋板运动的第二阶段(τT≤τ≤τf)。此时，。在满足τ=τT时刻的角位移和角速度的连续性条件下，运动方程的解经化简后为:

当τ=τf时，，加筋板的运动停止。由此可确定计算τf的表达式为:

将τ=τf值代入式(24)得到，再将代入式(27)，便可求得加筋板中点的永久变形值。

需要指出的是:以上给出的解是在满足正方形屈服条件(外接于精确的最大正应力屈服条件，图4中的实线)的前提下得到的。对应的屈服条件可表示为:

图4 理想塑性矩形截面的屈服曲线Fig.4 The interaction curves for rectangular section

由此得出的加筋板最大横向永久变形值将是最大正应力屈服条件解的上界［16］。如若采用内接于最大正应力屈服条件的正方形屈服条件(屈服应力取为0.618σy，图4中的点划线)，得出的最大横向永久变形值将是最大正应力屈服条件解的下界［16］。研究表明［16］:对于大的永久变形，有限横向位移的影响支配着结构的动力塑性响应。亦即膜力和轴力在响应中起到了主要的作用，从而可以完全忽略弯矩的影响，响应由膜力单独控制，对应的屈服条件成为N=N0和 M=M0。由此给出的解称之为塑性动力分析中的薄膜解。为此，在前面导出的运动方程(8)、(12)和(15)三式中令M0=0和M'0=0，便可得到薄膜解的相关方程。

双根加筋固支方板运动方程(12)和(15)式的求解类似于单根加筋固支方板运动方程的求解，这里不再详述。计算实例的计算结果列于表2中，包括解析解、薄膜解以及能量解的计算结果，表中同时列出了文献［3］的实验结果。

表1 计算模型的尺寸及外载荷Tab.1 Model size and the peak of load applied

表2 计算结果与实验结果［3］的比较Tab.2 A comparisons of the calculation results with experimental results

图5给出了截面尺寸为3mm×3mm加强筋模型(A00、A13、A17和A01)的中点永久变形 w0与爆炸载荷峰值q0之间的关系曲线。由图5可以看出:实验值全部落在满足外接以及内接正方形屈服条件的理论曲线之间，表明简单理论方法提供了最大永久变形的上界与下界。图5给出的结果还表明:忽略弯曲影响的薄膜解与能量解与实验值相当接近。由此证实了下述的结论:在大塑性变形的场合，膜力和轴力在加筋板的塑性动力响应中起到了主要的作用，从而可以完全忽略弯矩的影响。

分析表2给出的计算结果与实验结果可以看出，在多数情况下两者之间符合良好。表明本文给出的简化理论分析方法能对爆炸载荷下单根加筋固支方板的永久变形做出较为合理的预报。

图5 单根加筋固支方板的w0－q0关系曲线Fig.5 w0－ q0curve for build-in square plate with single stiffener

4 结论

通过理论推导和实例分析可以得到以下结论:

(1)本文提出的理论分析方法能对爆炸载荷下单根加筋固支方板的永久变形做出较为合理的预报，从而证实了本文提出的理论模型的合理性。

(2)本文提出的简化分析方法的特点是:分别列出加筋板的面板以及加强筋的运动方程，只考虑了面板与加强筋之间相互作用反力的传递，从而给加筋板的塑性动力响应分析工作带来很大的简化。需要指出的是:上述简化假定基本上是合理的。这是因为在大变形的条件下，影响加筋板结构变形性能的主要内力要素是面板中面内的膜力以及加强筋横截面内的轴力，忽略弯矩和剪力的相互传递不会对最终的计算结果带来重要的影响。

(3)本文提出的简化分析方法的优点是毋需复杂的数字运算，却能对爆炸载荷作用下加筋板结构的塑性动力响应做出合理的预报。将它应用于抗爆加筋板结构的初步设计以及优化设计将是很有用处的。

(4)本文将文献［14］和文献［15］提出的关于爆炸载荷作用下圆板的简化能量解法推广应用于单向加筋方板的场合，取得了很好的结果。但是，此种推广仅适用于加筋板总体变形模式的情况。对于发生加筋板板格局部变形与加筋板总体变形耦合运动的状况，因为涉及到局部破坏模式如何向总体破坏模式过渡的问题，能量法就显得有些无能为力了。本文提出的从分别列出加筋板板格以及加强筋的运动方程出发的简化分析方法可适用于此种情况的分析研究。

［1］Nurick G N，Olson M D，Fagnan J R，et al.Deformation and tearing ofblast-loaded stiffened square plates ［J］.International Journal of Impact Engineering，1995，16(2):273－291.

［2］Rudrapatna N S，Vaziri R，Olson M D.Deformation and failure of blast-loads stiffened plates［J］.International Journal of Impact Engineering，2000，24(5):457－474.

［3］Chung Kim Y S，Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.PartⅠ:Subjected to uniform blast load［J］.International Journal of Impact Engineering，2005，31(1):55 －83.

［4］侯海量，朱 锡，古美邦.爆炸荷载作用下加筋板的失效模式分析及结构优化［J］.爆炸与冲击，2007，(1):26－33.

［5］牟金磊，朱 锡，张振华，等.水下爆炸载荷作用下加筋板变形及开裂试验研究［J］.振动与冲击，2008，27(1):57－60.

［6］张振华，陈平毅，漆万鹏，等.舰船局部板架结构在水下爆炸冲击波下动态响应的相似律研究［J］.振动与冲击，2008，27(6):81 －86.

［7］Schubak R B，Olson M D，Anderson D L.Rigid-plastic modeling of blast-loaded Stiffened plates-PartⅠ:One-way stiffened plates and PartⅡ:Two-way stiffened plates［J］.International Journal of Mechanical Science，1993，35(3/4):289－324.

［8］刘土光，胡要武，郑际嘉.固支加筋方板在爆炸荷载作用下的刚塑性动力分析［J］.爆炸与冲击，，1994，14(1):55－65.

［9］刘土光，唐文勇.加筋板结构在冲击载荷作用下的塑性动力响应［J］.华中理工大学学报，1996，24(1):106－109.

［10］唐文勇，陈铁云.加筋板结构的塑性动力响应分析［J］.上海交通大学学报，1996，30(8):74－80.

［11］吴有生，彭兴宁，赵本立.爆炸载荷作用下舰船板架的变形与破损［J］.中国造船，1995，(4):55－61.

［12］方 斌，朱 锡，张振华.水下爆炸冲击波荷载作用下船底板架的塑性动力响应［J］.哈尔滨工程大学学报，2008，29(4):326－331.

［13］黄震球.固支加筋方板的大挠度塑性动力响应［J］.固体力学学报1995，(1):7 －12.

［14］Cloete T J，Nurick G N，Palmer R N.The deformation and shear failure of peripherally clamped centrally supported blast loaded circular plates.［J］.International Journal of Impact Engineering，2005，32(1):92－117.

［15］Duffey T A. The large deflection dynamic response of clamped circular plates subjected to explosive loading［R］.Sandia Laboratories research report，SC-RR-67 －532，1967.

［16］彭兴宁，聂 武，严 波.爆炸载荷作用下舰船防护舱壁的薄膜效应研究［J］.船舶力学，2007，(5):744－751.

［17］Jones N.Structural Impact［M］.Cambridge UK:Cambridge University Press，Cambridge，1989.(中译本:［英］诺曼.琼斯著.结构冲击［M］.蒋平译，王礼立校审.成都:四川教育出版社，1994).