基于灰色小波核偏最小二乘的传感器网络数据预测融合研究

康 健，唐力伟，左宪章，李 浩，张西红

(1.军械工程学院，石家庄 050003;2.72889部队，河南 新乡 453636;3.63880部队，河南 洛阳 471003)

传感器网络的发展受到包括能量供应、数据处理能力等诸多条件的限制和挑战［1］，这就决定了传感器网络难以传输大量的感知数据。如何有效地融合这些感知数据，去除冗余信息，减少网络传输量，优化网络性能，提高资源的利用率，从而延长网络生命周期，一直是传感器网络研究的重要课题。

在传感器网络中，可根据传感器节点采集的系统有限长度的运行记录，建立能够反映时间序列中所包含的动态依存关系的数学模型，并且对系统的未来行为进行预测。通过预测，减少不必要的数据传输，从而降低网络能耗，延长网络生命周期。在基于预测的传感器网络数据融合中，如何根据采集的数据类型进行数据样本及预测融合算法的选择是问题的关键所在。

Sharaf等人［2］提出了一种网内融合的机制TiNA(temporal coherency-aware in-network aggregation)。该机制对于监测数据波动较小的应用十分有效，能显著地减少网络中的数据传输量。然而，TiNA对于节点存储空间的要求比较高。Santini和Romer提出了一种基于最小二乘滤波的双重预测策略［3］，在资源节点和汇集节点同时实施此策略。Borgne等人［4］进一步发展了这种思想，提出了时间序列预测的自适应模型选择算法。该算法中，传感器节点自适应地从多个备用模型中选择性能最优的模型进行预测，取得了较好的效果。回春立和崔莉［5］提出了传感器网络中基于预测的时域数据融合技术。数据融合算法使用时间序列模型进行预测，模型的复杂度与网络规模无关，因此数据融合算法具有较好的可扩展性。

上述方法均未考虑到传感器网络采集到的数据的非平稳性、非线性、随机性以及突变情况。而灰色理论把一切随机变量、随机过程均看作灰色变量、灰色过程，具有处理随机过程、突变的能力。核偏最小二乘法既吸取了核函数能够拟合适应任意连续变化曲线的优点，又借鉴了偏最小二乘法能够有效解决自变量集合高度相关的技术［6］。核偏最小二乘法不仅能够有效实现自变量对因变量的整体预测，而且能够提取各维自变量对因变量的单独非线性作用特征，从而确定数据系统内部的复杂非线性结构关系，增强了模型的可解释性。因此，本文提出了一种基于灰色Morlet小波核偏最小二乘的预测融合模型(GMWKPLS)，综合运用了灰色理论处理随机过程、突变的能力以及核偏最小二乘法将非线性问题转化为拟线性问题，从整体拟合和结构分析上均达到较高的精度的优势，通过动态实时预测，减少数据传输量，从而降低网络能耗，延长网络的生命周期。

1 灰色建模机理

灰色预测模型是由灰色理论的微分方程所建立的。灰色系统理论运用基于关联度收敛原理、生成数、灰导数、灰微分方程等观点和方法建立了微分方程模型［7］，微分方程的系数则描述了人们所希望辨识的系统内部的物理或化学过程的本质。

灰色模型首先对原始序列进行累加生成(或累减生成)，将原始数据整理成规律性较强的生成序列再做研究。这种灰数的形成，就是从原始数据中去寻找其潜藏着的内在规律，这是一种现实规律，不是先验规律。然后利用规律性较强的生成序列建立预测模型，最后将所得预测结果进行“累减还原”，得到原始序列的预测值。

2 小波核偏最小二乘

2.1 核偏最小二乘

核偏最小二乘的基本思想是将输入通过非线性函数映射到高维特征空间，在特征空间再运用线性偏最小二乘算法，这样特征空间的线性PLS就对应原输入空间的非线性关系。

设有 p个自变量{x1，x2，…，xp}和 q个因变量{y1，y2，…，yq}，样本点 n个，构成自变量矩阵 X={x1，x2，…，xp}n×p与因变量矩阵 Y={y1，y2，…，yq}n×q。核偏最小二乘法首先将X进行核函数变换为K，然后分别在K和Y中提取成分 t1和 u1，t1和 u1分别是 k1，k2，…，kp和 y1，y2，…，yq的线性组合，并且 t1和 u1需满足下列要求:

(1)t1和u1应尽可能多地携带它们各自数据矩阵中的变异信息;

(2)t1和u1的相关程度能够达到最大。

在第一个成分t1和u1被提取后，核偏最小二乘法分别实施K对t1的回归以及Y对t1的回归，如果回归方程已经达到满意的精度，则算法终止;否则，将利用K被t1解释后的残余信息以及Y被t1解释后的残余信息进行第二轮的成分提取。如此循环，直到能达到一个较满意的精度为止。若最终对K共提取了m个成分t1，t2，…，tm，偏最小二乘法将通过实施 Y 对 t1，t2，…，tm的回归，然后再表达成Y关于原变量k1，k2，…，kp的回归方程，至此核偏最小二乘建模完成。

2.2 Morlet小波核的构造

核是定义在原始空间的一个双变量函数，但它却实现了某一高维空间的内积，提供了把线性学习机扩展到非线性学习机的手段。Mercer定理给出了一种判定核函数正定的条件，而现有的KPLS方法大都使用高斯RBF核函数，即k(x，z)=exp(－/σ2)，实现具有非线性变换的偏最小二乘算法。本文基于小波分析技术，采用对数据变化趋势刻画能力较强的Morlet母小波来构造小波核函数，以提高其学习性能。在Mercer定理基础上，首先给出判断和构建核函数的定理 1 和定理 2［8－9］。

定理1 平移不变核函数k(x，z)=k(x－z)是一个允许的支持向量核函数，当且仅当傅里叶变换

成立。

定理2 若ψ(x)为母小波函数，伸缩因子为σ，平移因子分别记为 m 与 d，其中 m，d，x，z∈RN，xi，zi，σ，mi，di∈R，则下式给出的满足平移不变性定理的张量积小波核是可允许的多维支持向量核函数

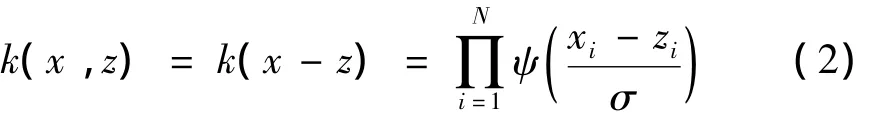
为构造一种平移不变小波核函数，不失一般性，可选择Morlet母小波，即:

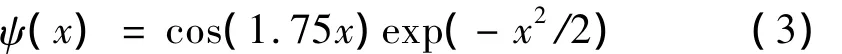
其中，N为输入x的维数。

定理3 若给定Morlet母小波函数如(3)式所示，伸缩因子为 σ，其中 x，z∈RN，σ，xi，zi∈R，则下式所表示的小波核函数就是一种可允许的多维张量积的支持向量核函数

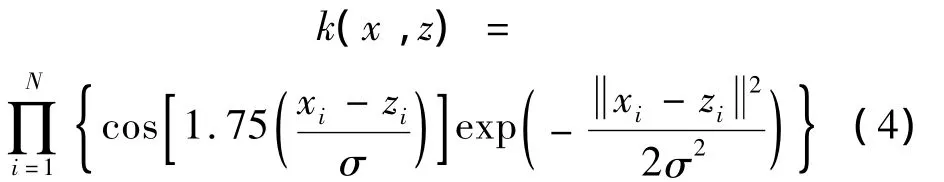
证明:

根据定理1和定理2，只需证下列不等式成立即可:

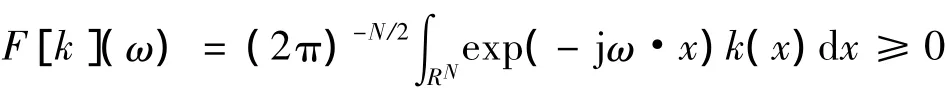
其中:

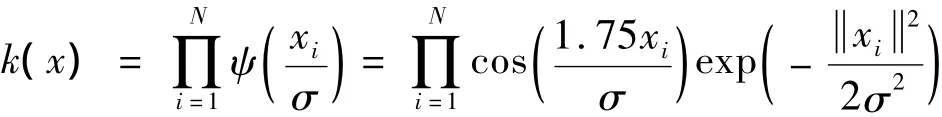
利用欧拉(Euler)公式ejx=cosx+jsinx以及

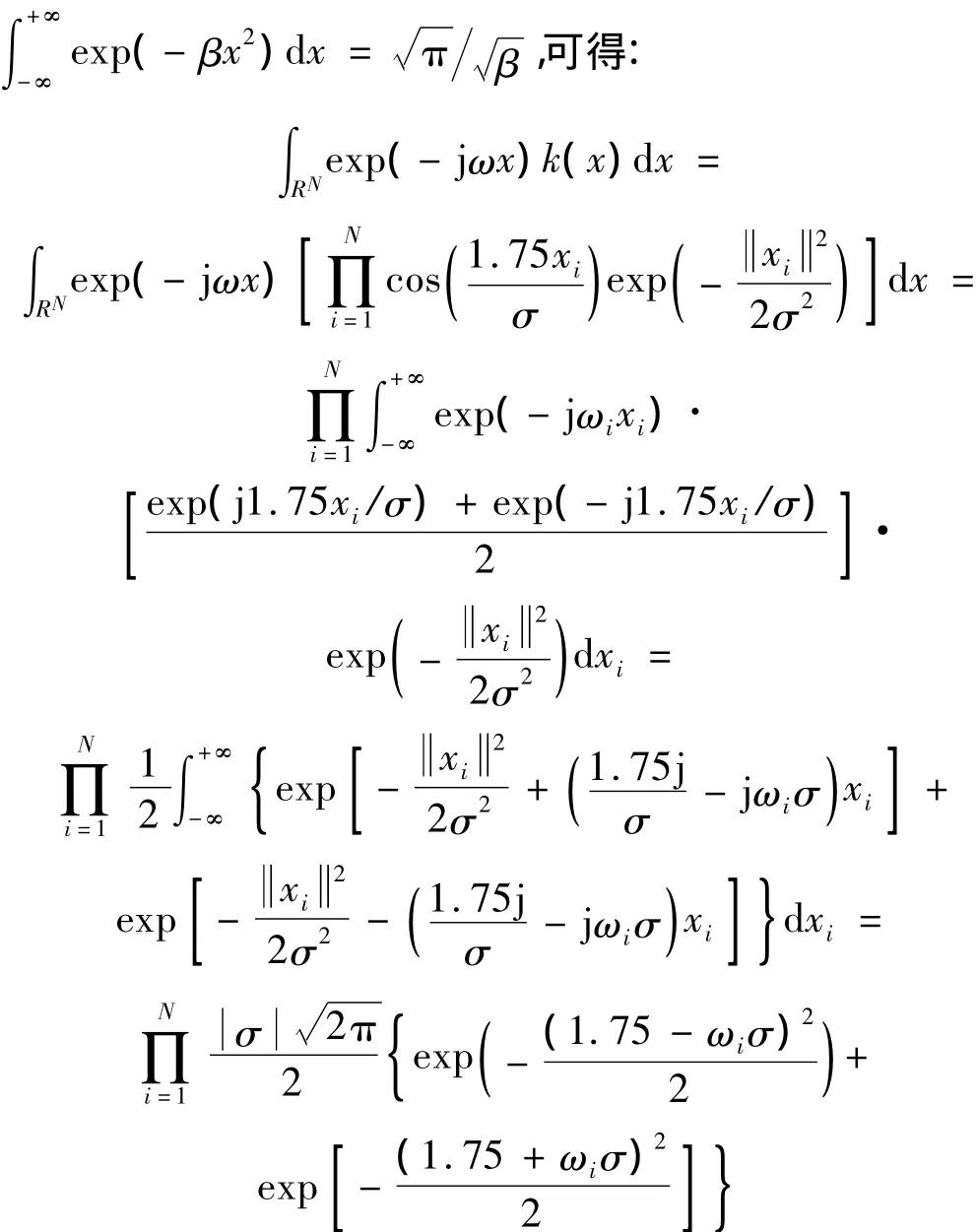
则小波核函数的傅里叶变换为:

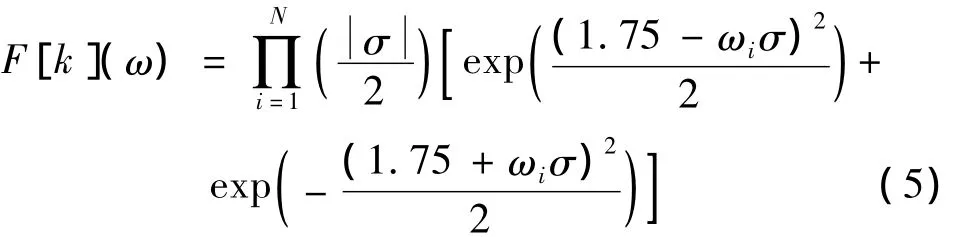
又因为伸缩因子(尺度参数)σ≠0，且N≥1，所以F［k］(ω)=≥0。证毕

3 预测融合模型

定义:时间序列 T={x1，x2，…，xN}，其中 xi为第 i时刻的数值，i=1，2，…，N。

对于给定的时间序列{x1，x2，…，xN}，假设已知xi预测xi+1，则可以建立映射:

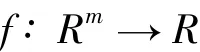
满足:

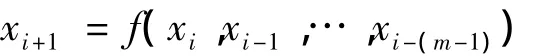
其中，m称为嵌入维数，即模型的阶数。采用最终误差预报准则(Final Prediction Error，FPE)评价模型的预测误差，并根据误差大小选取嵌入维数m。经过变换后，得到用于预测器学习的样本:

灰色Morlet小波核偏最小二乘预测模型(GMWKPLS)的设计思想如下:首先利用灰色预测方法将原始序列进行一次累加生成，得到生成序列;然后利用Morlet核偏最小二乘法拟合非线性数据能力的优势对生成序列建立预测模型;最后将预测结果进行累减还原得到预测值，并根据数据的动态增减策略，更新原始数据序列，进行循环运算。

预测模型建立的具体步骤如下:

步骤1:数据灰色处理。首先对采样原始序列X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，x(0)(i)＞0，i=1，2，…，n，进行一次累加得生成序列 X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}，其中:2，…，n。根据上述预测器学习样本建立的方法，将累加生成序列作为GMWKPLS的学习样本X和Y。

步骤2:数据标准化和Morlet核变换处理。对生成序列数据做标准化处理，即对数据同时进行中心化——压缩处理。然后对标准化处理后的自变量数据矩阵 E0=(E01，E02，…，E0p)n×p，进行 Morlet小波核函数变换，得变换后的核数据矩阵 K0=(K01，K02，…，K0p)n×p。记标准化处理后的因变量数据矩阵为F0=(F01，F02，…，F0q)n×q。标准化公式如下

步骤3:提取成分，建立预测方程。记t1、u1分别是K0、F0的第一个成分，求解 t1=K0w1，u1=F0c1。其中，w1、c1分别是K0的第一个轴和F0的第一个轴，并且是最大特征值对应的单位特征向量，即然后，分别求K0和 F0对 t1和u1的两个回归预测方程:

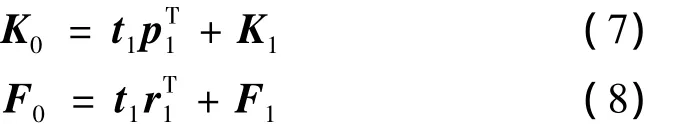
步骤4:循环提取成分。用残差矩阵K1和F1取代K0和F0，然后求第二个轴w2和c2以及第二个成分t2、u2和相应的回归预测方程。其中

步骤5:模型验证。进行交叉有效验证(Cross Validation)，确定提取的成分数。一般采用舍一交叉验证。如通过验证，转到步骤4提取下一个成分;否则，转到步骤6。

步骤6:预测方程模型。如果K的提取的成分个数为A，则有:

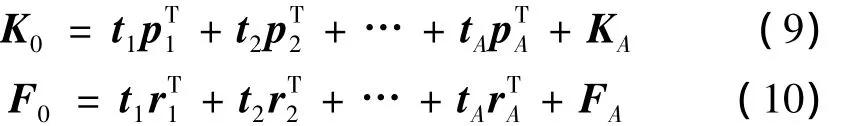
由于 t1，…，tA均可由 K1，…，KA线性表示，所以式(10)可以还原成K的线性表达式，得到最终的多维输入多维输出预测模型:

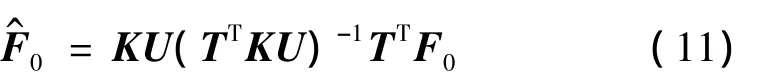
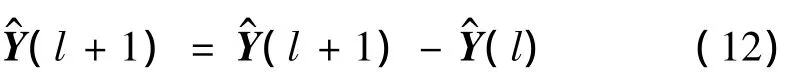
其中，l=m+1，m+2，…，n。

步骤8:更新数据。使用滑动窗方法动态地增减X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}中的数据，对其进行更新，然后，从步骤1进行循环运算。

4 实验和预测结果

4.1 测试数据的获取

在齿轮箱故障诊断实验台上，测得齿轮箱主动齿轮(小齿轮)出现断齿情况下的升速过程中的时域振动信号，如图1所示。由信号的波形可以看出:其幅值随着转速的波动而变化，是一个明显的非平稳过程。

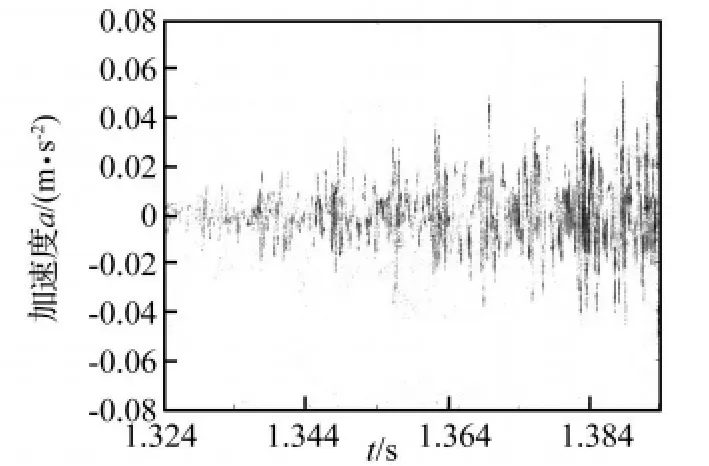
图1 齿轮箱断齿工况升速过程中振动信号Fig.1 Vibration signals of gear tooth breakage in speed of rising

4.2 预测融合结果

选取振动信号的前600个数据作为样本数据，后300个数据作为预测数据。在GMWKPLS预测融合模型中，采用构造的Morlet小波核函数，其中，核函数参数σ =4，潜在特征参数为8。随着预测融合的进行，对历史数据进行了动态更新，依据最终误差预报准则，采取单步预测策略。这样做的主要目的是保证预测结果具有较高的精确性和可靠性。

为了对比预测精度和有效性，还使用灰色RBF核偏最小二乘模型(GRBFKPLS)和RBF核偏最小二乘模型(RBFKPLS)对原始数据进行预测融合，对比情况如图2～图7所示。其中，GRBFKPLS的核函数参数为σ =2.6，潜在特征参数为13;RBFKPLS的核函数参数为 σ =0.08，潜在特征参数为18。

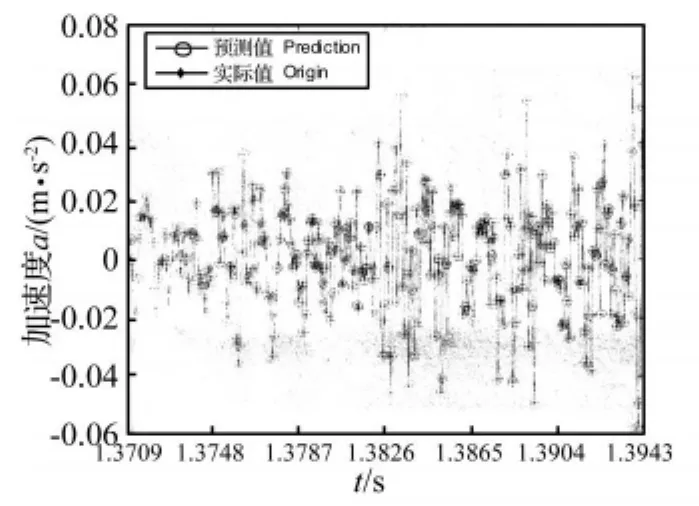
图2 GMWKPLS预测值与实际值Fig.2 The values of prediction and origin for GMWKPLS

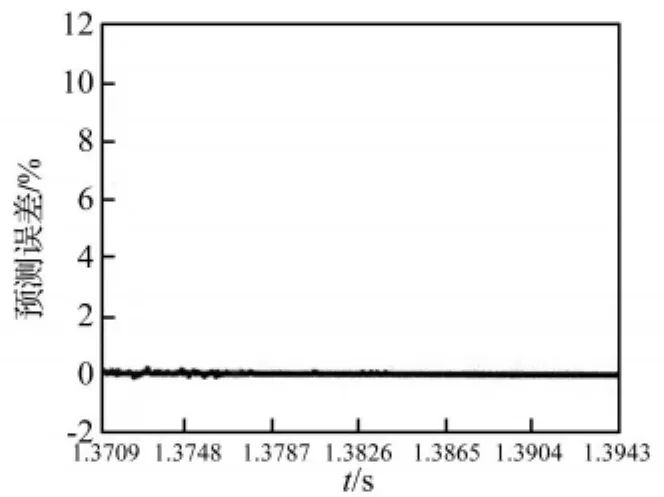
图3 GMWKPLS预测误差Fig.3 Prediction error of GMWKPLS

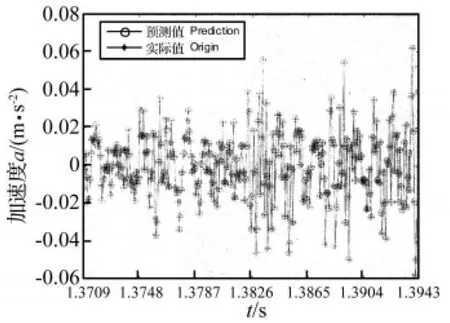
图4 GRBFKPLS预测值与实际值Fig.4 The values of prediction and origin for GRBFKPLS

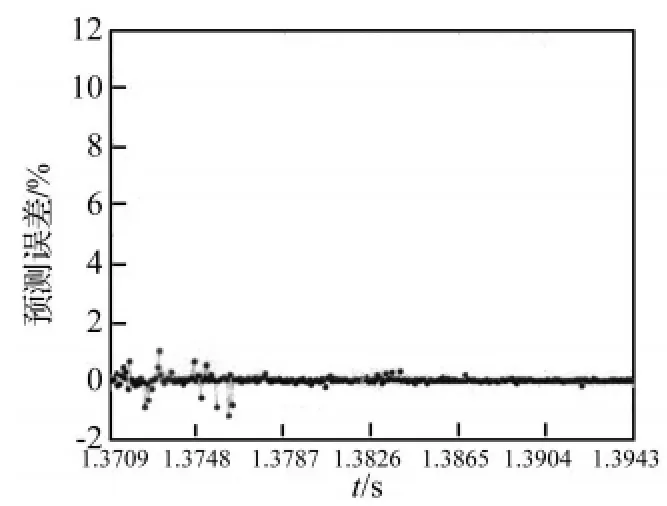
图5 GRBFKPLS预测误差Fig.5 Prediction error of GRBFKPLS

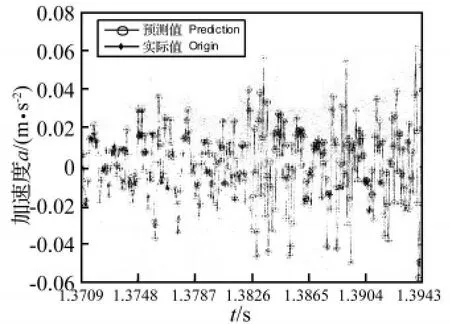
图6 RBFKPLS预测值与实际值Fig.6 The values of prediction and origin for RBFKPLS

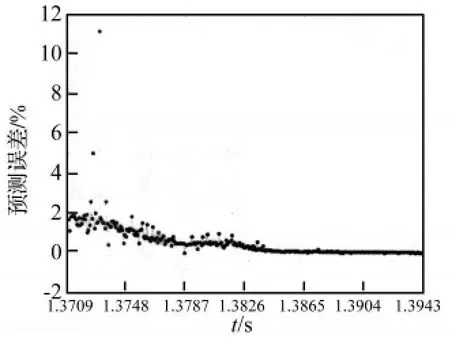
图7 RBFKPLS预测误差Fig.7 Prediction error of RBFKPLS

从图2～图7中可以看出，采用GMWKPLS取得的预测效果比GRBFKPLS和RBFKPLS的都好。GMWKPLS的预测误差最小，其次为GRBFKPLS，而RBFKPLS的预测误差最大。GMWKPLS和GRBFKPLS的预测误差比RBFKPLS的预测误差小得多。GMWKPLS的预测误差范围在±0.15%以内，GRBFKPLS的预测误差范围在 ±1.5%以内，而 RBFKPLS的最大预测误差超过10%。

其次，由于采用的是断齿工况升速过程振动信号，开始所用数据不能表示后面数据大幅变动的特征现象，从而导致误差曲线在1.3709 s～1.3787 s之间会有些振荡。然而，随着动态更新数据，一旦更新后的数据能够表示信号的本质特征，误差曲线中的振荡就会消失，误差曲线就会趋近于平稳状态。

另外，通过进一步分析，在GMWKPLS中，预测误差的大小与数值的突变程度近似成正比。而在GRBFKPLS和RBFKPLS中，这种规律却不明显，也就是说预测模型的可靠性不高，原因在于数据的随机波动对预测模型的建立有一定的影响。

5 分析与讨论

5.1 性能评价

从平均绝对百分误差(mean absolute percentage error，MAPE)、均方根误差 (root mean squared error，RMSE)和均方根相对误差(root mean squared relative error，RMSRE)3个方面对3种预测模型预测性能进行比较，见表1。均方根误差可以比较预测器的逼近能力，而平均绝对百分误差、均方根相对误差用来评价模型的预测效果及计算的准确率。

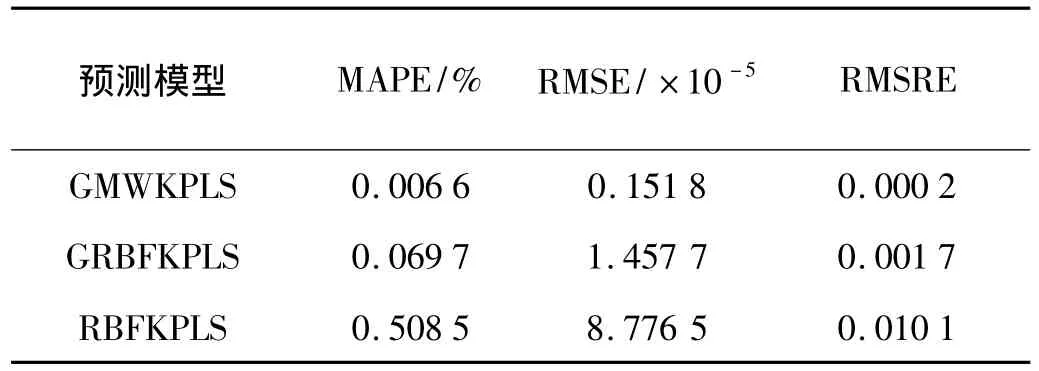
表1 预测模型性能评价指标Tab.1 Performance evaluation of prediction model

从表1中可以看出，GMWKPLS的性能最优，其次为GRBFKPLS，而RBFKPLS的性能最差。与GRBFKPLS和 RBFKPLS相比，GMWKPLS和 MAPE、RMSE和RMSRE均小得多，相差一个或两个数量级。这表明所建GMWKPLS预测模型具有较强的逼近能力、较高精确度及较好预测效果。究其原因，在GMWKPLS中，由于首先采用灰色预测中“累加生成”的方法，削弱原始数据序列中随机扰动因素的影响，使离乱的原始数据中蕴涵的规律充分显露出来，增强数据的规律性。其次，KPLS不仅能够有效实现自变量对因变量的整体预测，而且能够提取各维自变量对因变量的单独非线性作用特征，从而确定数据系统内部的复杂非线性结构关系，增加了模型的可解释性。最后，采用对数据变化趋势刻画能力较强的Morlet小波核函数，可以提高模型的学习性能。所以，综合了灰色理论、KPLS和Morlet小波核的各自优势的GMWKPLS预测模型表现出的预测性能最佳。

通过对预测模型性能评价指标的分析，验证了本文所建模型的正确性和可靠性。

5.2 节能分析

传感器网络预测融合的主要目的就是降低数据传输量，从而节省网络能量，延长网络的生命周期。每次运行GMWKPLS程序大约需执行22500条指令。在传感器网络中，发送1 bit的信息所消耗的能量等于执行2000条指令［10］。设定发送的数据包为 8 bytes(64 bits)，耗能320 nJ，则可执行128000条指令，相当于执行大约6次GMWKPLS程序。表2为在预测误差允许范围内，GMWKPLS节能情况分析。

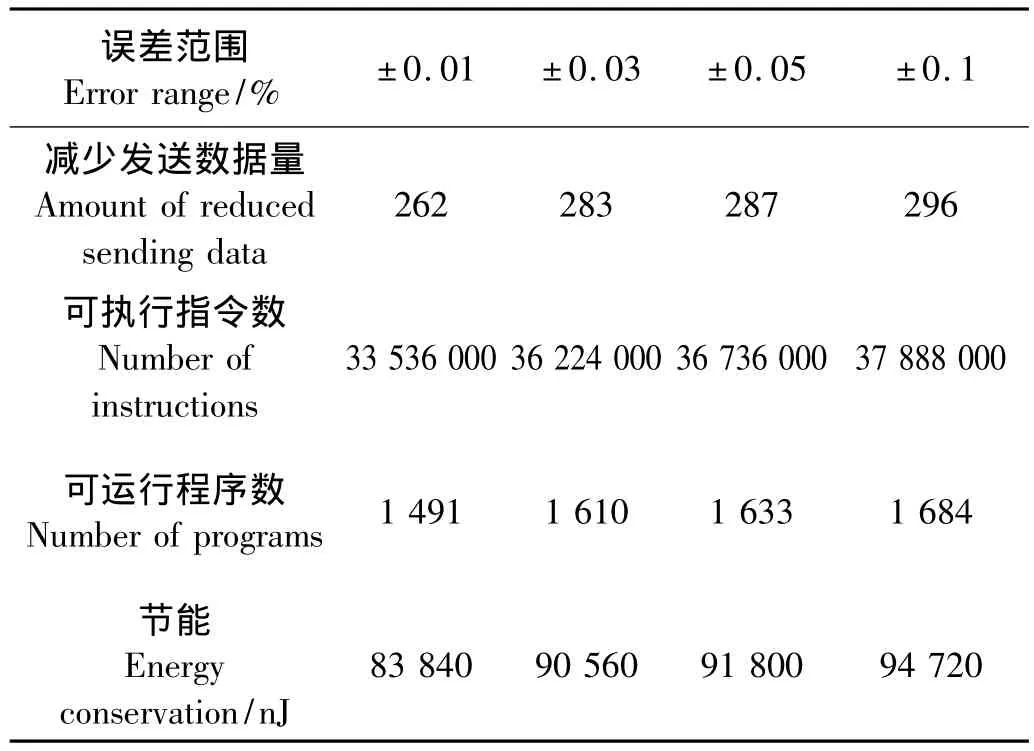
表2 预测模型节能情况Tab.2 Energy evaluation of prediction model

经过这些简单的估算，可知不但计算耗能能从通信节能中得到补偿，而且预测模型能显著降低网络耗能，节省网络能量。

另外，在GMWKPLS预测融合模型中，因其预测精度高，并能进行动态预测，不但减少了数据发送的能量消耗，而且节省了部分采样的能量消耗，从而延长网络生命周期，具有广阔的应用前景。

6 结论

通过预测融合来减少传感器网络中的不必要的数据传输是传感器网络数据融合研究的主要方向。本文提出了一种GMWKPLS预测融合建模方法，它将灰色模型预测的思想融入了KPLS中，从原始数据中去寻找其潜藏着的内在规律，使其具有处理随机过程、突变的能力;它通过构造Morlet小波核函数，保持了小波函数近似正交及多分辨分析的优点，能够更好地展现输入与输出数据之间的非线性映射关系，实现整体预测功能，其建模能力优于GRBFKPLS和RBFKPLS方法。

通过对传感器网络采集到的振动信号进行动态预测，结果表明，GMWKPLS预测的振动幅值趋势与实际曲线基本相符，预测误差范围在±0.15%以内。因此，采用该模型可以显著减少数据传输量，从而降低网络能耗，延长网络的生命周期。GMWKPLS为传感器网络数据预测融合及提高预测融合性能提供了一种新途径。

［1］Nakamura E F，Loureiro A F，Frery A C.Information fusion forwireles wensor networks:methods， models， and classifications［J］.ACM Computing Surveys，2007，39(3):1－55.

［2］Sharaf M A，Beaver J，Labrinidis A，et al.TiNA:a scheme for temporal coherency aware in network aggregation［C］//Proceedings of the 3rd ACM International Workshop on Data Engineering for Wireless and Mobile Access.San Diego:ACM，2003:69－76.

［3］Santini S，Romer K.An adaptive strategy for quality－baseddata reduction in wireless sensor networks［C］//Proceedings of the 3rd International Conference on Networked Sensing Systems.TRF，Chicago，IL:ACM，2006:29–36.

［4］Le Borgne Y A，Santini S，Bontempi G.Adaptive model selection for time series prediction in wireless sensor networks［J］.Signal Processing，2007，87(12):3010 －3020.

［5］回春立，崔 莉.无线传感器网络中基于预测的时域数据融合技术［J］.计算机工程与应用，2007，43(21):121－125.

［6］孟 洁，王惠文，黄海军，等.基于核函数变换的PLS回归的非线性结构分析［J］.系统工程，2004，22(10):93－97.

［7］Luo Y X，Zhang L T，Cai A H，et al.Grey GM(1，1)model with function－transfer method and application to energy consuming prediction ［J］.Kybernetes，2004，33(2):322－330.

［8］Zhang Li，Zhou Wei－da，Jiao Li－ cheng.Wavelet support vector machine ［J］.IEEE Transactions on systems，man，and cybernetics，2004，34(1):34－39.

［9］李 军，董海鹰.基于小波核偏最小二乘回归方法的混沌系统建模研究［J］.物理学报，2008，57(8):4756－4765.

［10］Raybunatban V，Schurgers C，Park S，et al.Energy－aware wireless microsensor networks［J］.IEEE Signal Processing Magazine，2002，19(2):40－50.