交通环境振动观测中本底振动去除的功率谱修正法

王福彤，陶夏新，郑 鑫，3，崔高航，陈宪麦

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090;2.黑龙江大学 建筑工程学院，哈尔滨 150001;3.黑龙江八一农垦大学 工程学院，大庆 163319;4.东北林业大学 土木工程学院，哈尔滨 150040;5.中南大学 土木建筑学院，长沙 410075)

公路、轨道交通系统引起的环境振动问题日益受到人们的关注。目前的研究手段主要集中于理论分析、数值模拟和现场实测三方面［1］。现场观测数据是环境振动评价的直接依据，而且能为理论分析和数值模拟提供验证。然而通过观测获得的数据不单单包含交通系统引起的振动，还不可避免地含有附近工厂机器设备产生的振动、建筑工地施工产生的振动、地脉动(microseisms)以及由观测设备观测方法产生的观测误差。此类干扰振动或误差通常称为本底振动或暗振动。一般认为［3－5］，在距离交通线路非常近的区域本底振动的影响才可以忽略，而在距离稍远区域必须考虑本底振动的影响。为了考查场地土层速度结构等因素对环境振动的影响，必须保证若干测点与线路有一定距离，本底振动必然对观测数据产生干扰。只有有效地清除这些干扰因素，对实测数据进行修正，才能对交通系统诱发的环境振动问题作出准确和客观的分析［6］。

对于频率范围不相重叠的真实振动和本底振动，传统的滤波方法能够有效地去除本底振动。交通系统引起的真实振动(以下简称为真实振动)与本底振动往往在低频段内相互重叠，滤波方法难以达到令人满意的效果。张昕［2］、邱俊杰［7］、崔高航等［4］采用振动级修正法去除本底振动。该方法假设所有本底振动由一个振源引起，推导观测振动加速度级、真实振动加速度级和本底振动加速度级的关系，利用观测的总加速度数据和本底加速度数据计算真实振动加速度级。该方法能快捷有效地计算真实振动加速度级VAL以及振级VL，但不能获得真实振动的时程和功率谱密度。张向东等［6］为了获取真实振动的时程，提出了消除本底振动的Fourier谱幅值修正法(简称谱幅值修正法)。他们用观测振动谱幅值减去本底振动谱幅值，得到相应的不含本底振动的幅值，对其进行逆Fourier变换，得到真实振动的时程。本文假设交通系统引起的环境振动与其他因素引起的本底振动为互不相关的随机过程，通过对观测功率谱密度的修正达到去除本底振动的目的，并分别采用谱幅值修正法、振动级修正法以及本文建议的功率谱修正法对设定算例进行了比较分析。

1 功率谱修正法的计算公式

总的环境振动由交通系统引起的环境振动和由其他因素引起的环境振动两部分组成，所以

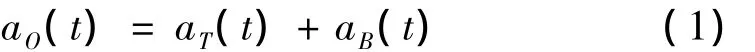
式中:aO(t)为观测总加速度时程;aT(t)为交通系统引起的真实振动加速度时程;aB(t)为本底加速度时程;aO(t)和aB(t)可通过观测设备获得观测序列;aT(t)无法直接测得。

对(1)式两边做Fourier变换，

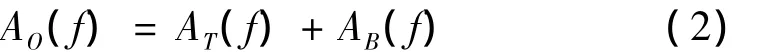
其中A(f)表示a(t)的Fourier谱。对式(2)两边求幅值的平方，

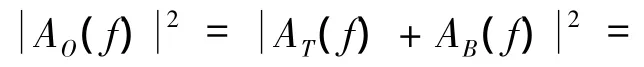
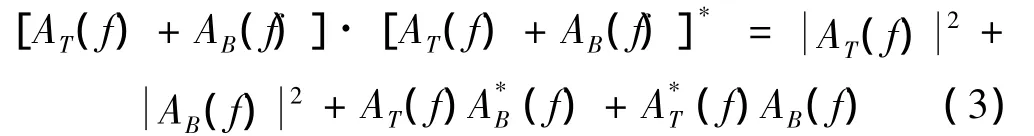
观测信号中本底成分的激励源构成十分复杂，传播路径传播方向各异。本底成分既包括海洋潮汐等自然源产生的低频microseisms，又包括工厂生产等人类活动源产生的高频microtremors，还包括由观测设备与方法产生的观测误差影响。真实振动由被观测的交通系统产生，相对于本底振动而言，振源与传播路径相对固定。从简化分析的角度出发，本文假定真实振动与本底振动是不相关的随机过程。因此，

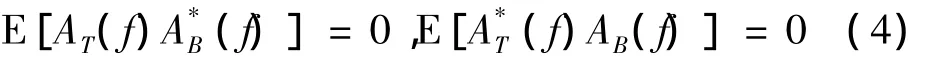
对式(3)求期望，并注意到式(4)，

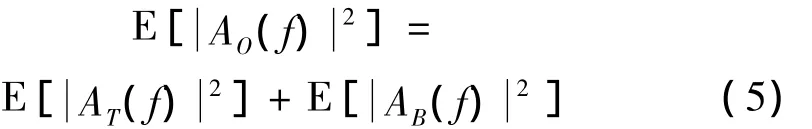
两边除以振动持时T得:

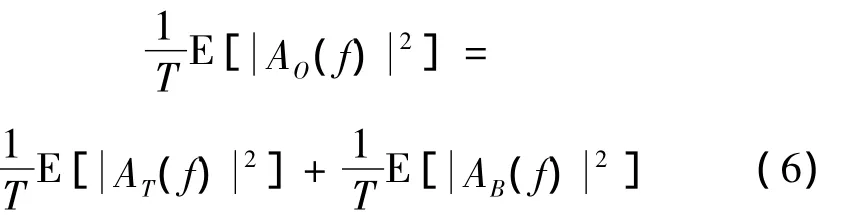
或写成:

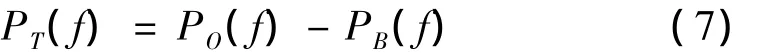
2 方法可靠性的验证及对比分析

2.1 验证方法与算例

为了考查本文方法的可靠性，首先取一条加速度时程并计算其功率谱和振动级，作为真实振动的设定曲线。另取一条在无车辆运行期间获得的加速度时程曲线作为本底振动，叠加到加速度时程设定曲线生成“观测”振动数据。然后假设真实振动未知，分别根据(7)式、振动级修正法和谱幅值修正法求真实振动的计算曲线，比较计算曲线与设定曲线，判断方法的可靠性，比较方法的准确性。

图1展示了作为算例的加速度时程曲线，分别为真实振动的时程设定曲线a'T(t)，本底加速度时程aB(f)，以及叠加生成的观测加速度时程 aO(t);图2为相应的功率谱密度P'T(f)、PB(f)和PO(f);图3为1/3倍频程中心频率处振动加速度级 VAL曲线，经ISO2631/1－1985竖向计权因子处理后的振级VL分别等于60.080 dB(设定的真实振动)、49.910 dB(本底振动)、60.440 dB(观测振动)。

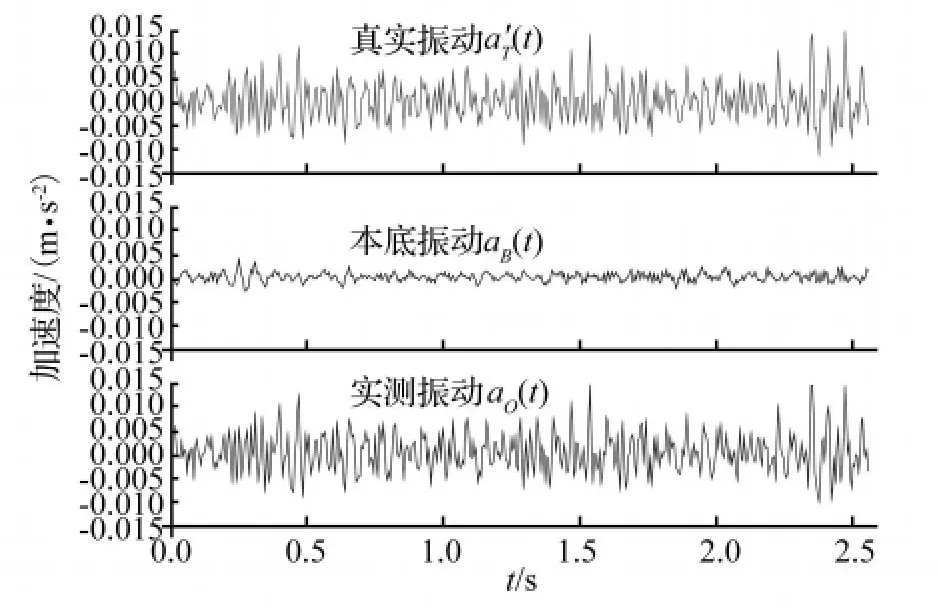
图1 算例的时程曲线Fig.1 Setting acceleration time histories for calculating example

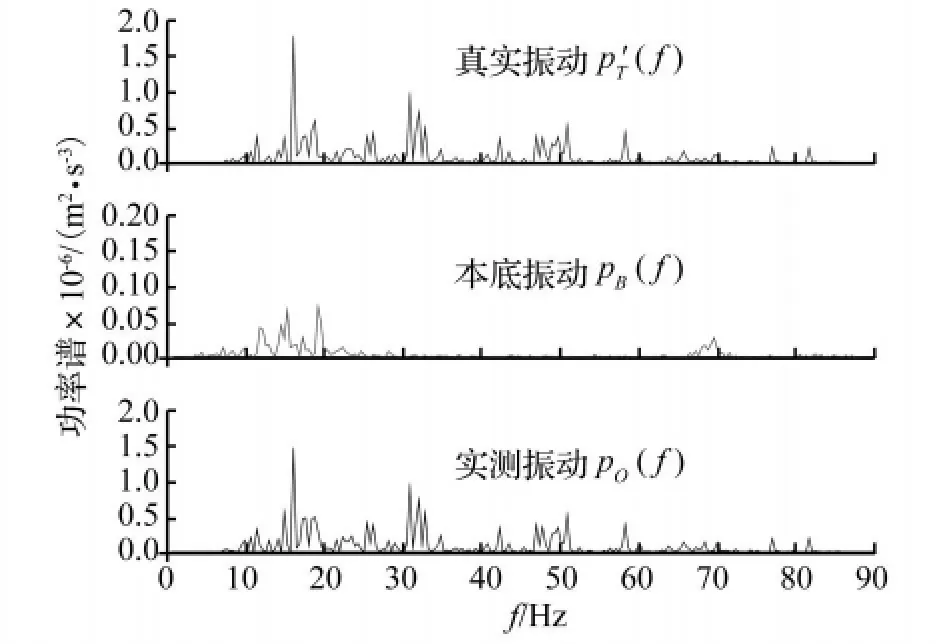
图2 算例的功率谱密度曲线Fig.2 Setting PSDs for calculating example

2.2 计算结果与讨论

2.2.1 功率谱的比较

按照(7)式计算得到真实振动功率谱计算曲线PT(f)绘于图4，可见PT(f)与设定曲线P'T(f)基本符合，表明功率谱修正法的计算结果是可靠的。

根据谱幅值修正法得到修正后的谱幅值，进而也得到真实振动的谱密度。定义功率谱的绝对误差为:

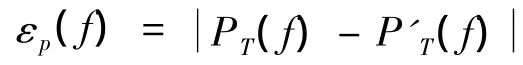
图5比较了两种方法的绝对误差。从图中可见，功率谱修正法的误差明显低于谱幅值修正法的误差，说明相对于谱幅值修正法而言，功率谱修正法具有更好的准确度。

2.2.2 时程的比较

从功率谱到时程的计算需要补充相位信息。谱幅值修正法计算时程的做法是把观测振动的相频曲线当做真实振动的相频曲线。本文亦采用该方式获取相位信息。图6分别显示了功率谱修正法与谱幅值修正法计算的加速度时程，可见两种方法的计算曲线aT(t)与设定曲线a'T(t)都很接近，功率谱修正法的结果更靠近设定曲线。定义加速度时程的绝对误差为:

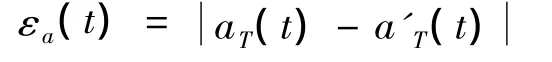
两种方法的绝对误差展示在图7中。从中可见在大多数时间点上，功率谱修正法的误差均显著低于谱幅值修正法的误差。

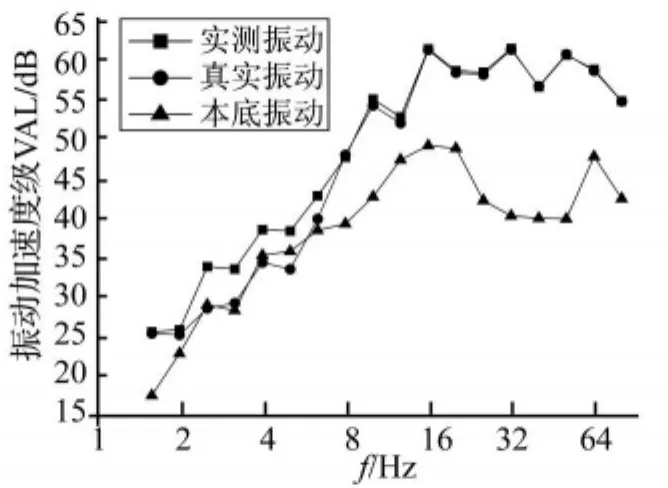
图3 算例的三分之一倍频程中心频率处振动加速度级VALFig.3 Vibration acceleration levels on one-third octave band centre frequency

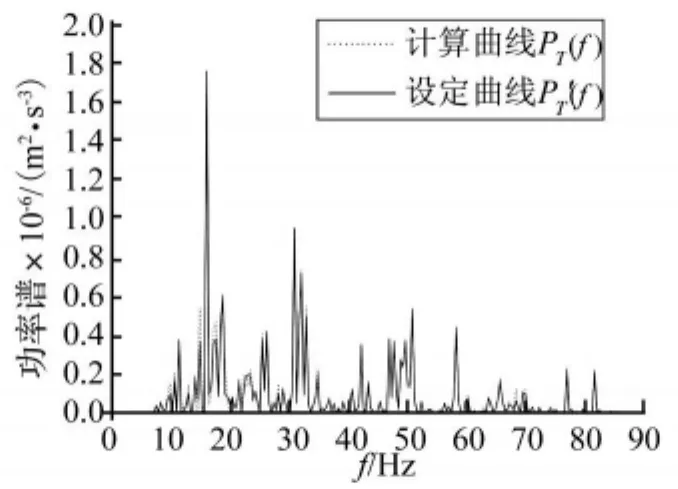
图4 功率谱的计算曲线与设定曲线的比较Fig.4 Comparison of calculated PSD with its setting value

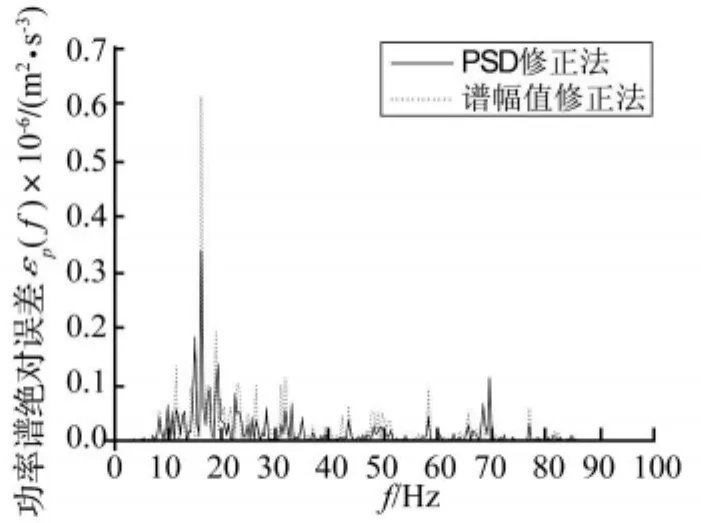
图5 功率谱的计算误差Fig.5 PSD calculating errors of PSD revising approach and Fourier amplitude revising approach

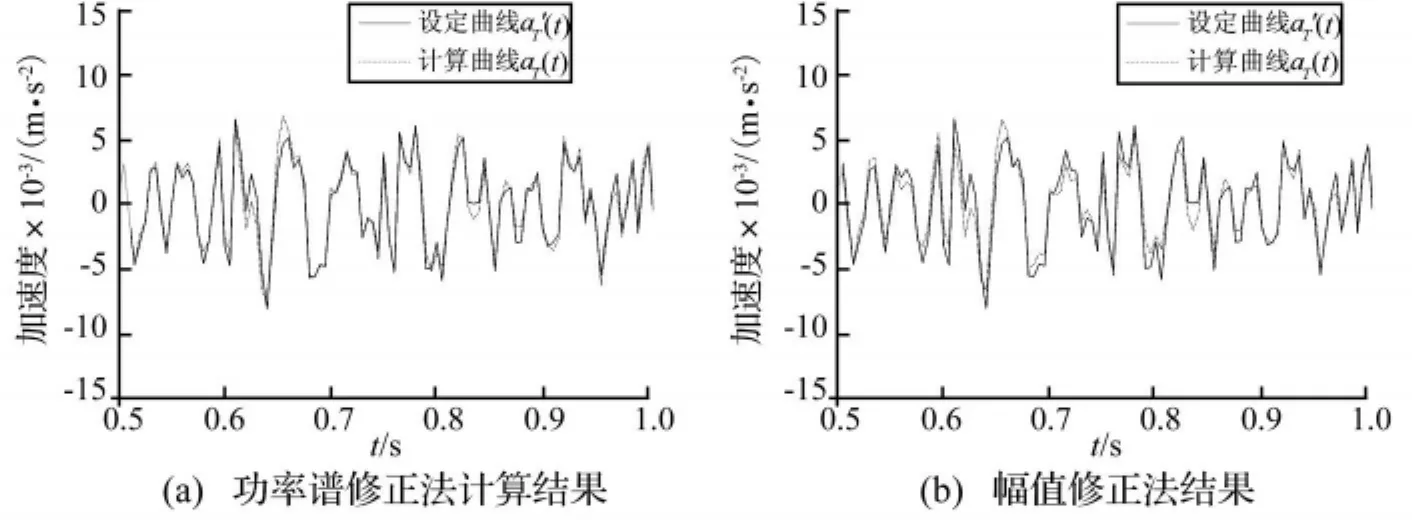
图6 加速度时程计算曲线与设定曲线比较Fig.6 Comparison of calculated acceleration time histories with the setting one

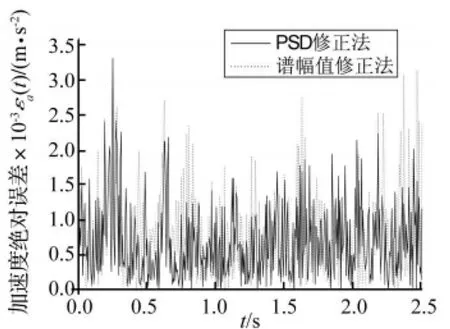
图7 加速度时程计算曲线的绝对误差Fig.7 Time history calculating errors of PSD revising approach and Fourier amplitude revising approach

2.2.3 振动级的比较

分别根据功率谱修正法和谱幅值修正法得到的功率谱计算了1/3倍频程中心频率处的VAL，同时采用振动级修正法计算了1/3倍频程中心频率处的VAL。图8展示了三条计算曲线与振动级设定曲线的对比。功率谱修正法和振动级修正法的结果与设定曲线十分接近，在高频部分完全吻合。除个别频点外，谱幅值修正法在大多数频点的误差略大，且该误差均为负值，说明谱幅值修正法有可能略低估计由交通系统引起的环境振动。

三条曲线经竖向计权因子处理后的振级VLz分别等于60.086 dB(功率谱修正法)、60.038 dB(振动级修正法)、58.603 dB(幅值修正法)。相比于设定值60.080 dB，本文方法的计算结果最为接近。

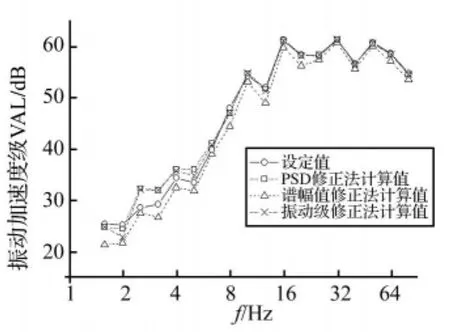
图8 三种方法计算的振动级Fig.8 Comparison of calculated VALs with the setting one

3 结论

为了有效地将本底振动从观测数据中剥离出去，提取交通系统引起的环境振动真实数据，本文提出了功率谱修正方法去除本底振动，并与谱幅值修正法、振动级修正法进行了比较，结果表明，

(1)功率谱修正法能够去除观测数据中的本底干扰，获得真实振动的功率谱和时程曲线，从而也能够得到1/3倍频程中心频率处振动级VAL以及加权振级VL，克服了振动级修正法的不足。

(2)对于谱密度和时程的计算，功率谱修正法的计算结果比谱幅值修正法的结果更为准确;对于振动级的计算，功率谱修正法和振动级修正法大体相当，优于谱幅值修正法。

鉴于问题的复杂性，本研究假定真实振动与本底振动为互不相关的随机过程。二者的相关性及其对分析结果的影响程度仍需做进一步深入研究。

［1］闫维明，聂 晗，任 珉，等.地铁交通引起地面振动的实测与分析［J］.铁道科学与工程学报，2004，3(2):1－5.

［2］张 昕.高架轨道交通引起环境振动的实测和理论分析研究［D］.上海:同济大学，2002，30－40.

［3］谢伟平，赵 伟，陈无平.关于《环境影响评价技术导则:城市轨道交通》中若干问题的探讨［J］.华中科技大学学报(城市科学版)，2007，24(2):1 －8.

［4］崔高航，陶夏新，陈宪麦.城轨交通地面线路产生环境振动频域分析［J］.沈阳建筑大学学报(自然科学版)，2008，24(2):239－243.

［5］蒋 通，张 昕.高架轨道交通引起环境振动的实测与数值模拟［J］.同济大学学报，2004，32(5):565－569.

［6］张向东，闫维明，任 珉，等.交通环境振动测试中的本底振动分析［J］.振动与冲击，2009，28(4):177－179.

［7］邱俊杰.高架轨道交通引起环境振动的实测与评价方法研究［D］.武汉:武汉理工大学，2005.