任意量子演化过程中的几何相位特征
王 鹏,贾培军
(1.延安大学 物理与电子信息学院;2.延安大学资产与实验室管理处,陕西 延安 716000)
任意量子演化过程中的几何相位特征
王 鹏1,贾培军2
(1.延安大学 物理与电子信息学院;2.延安大学资产与实验室管理处,陕西 延安 716000)
给出了任意量子演化过程中的几何相表达式。证明了几何相的测量不变性与消失特性。在任意量子演化过程中不仅观察到了几何相,还发现有其它几何结构,诸如长度和距离等几何结构也存在。指出了所有这些几何量之间的关系。
几何相位;量子演化;几何结构
自从 Berry[1]发现量子系统经过绝热、周期和参量变化可以获得重要的相位因子以后,人们开始寻找量子系统经历周期演化所获得的几何结构。这里的几何结构指那些与参量时间关系无关的量。Berry相位是具有这样本质的一种几何结构。根据厄米线束中的平行输运完整性可以很好地解释 Berry相位。Aharonov和Anandan(AA)在不考虑哈密顿量参量的绝热和周期演化情况下证明了几何相的存在[2]。AA相被认为是希尔伯特空间 Q的投影 P中围绕闭合曲线平行输运的完整变换。后来,由于人们发现几何相的完整性可以实现容错量子门[3,4],这使得几何相的完整性成为人们关注的热门课题,从而导致了对量子计算[5-9]和 量子 信息[10-13]中完整效应的研究。
Samuel和 Bhandari在薛定谔、非周期、非归一演化条件下得到了几何相[6]。然而,该几何相是个间接定义,取决于开路径的初末点的简单闭合。如果末点不闭合,那么该几何相就不再具有测量不变性。Anandan等人利用群理论基石在投影的希尔伯特空间 P中获得了任意演化几何相的无限小角元。Aitchison以非动力学方式定义了薛定谔、非周期、非归一演化几何相[7]。后来,Mukunda给出了几何相动力学方法的一般理论[8]。
本文主要研究了任意演化量子系统所获得的几何相位、距离、长度。给出了非周期演化的意义,并给出了薛定谔、任意演化几何相的定义。利用投影希尔伯特空间 P中线束定义了参考项,并证明通过联络一形式的线性积分给出了几何相表示。指出了几何相的各种特征;证明了几何相不仅是相位不变的,而且是测量不变的;还证明了几何相的消失特性。另外,引入了任意量子演化的几何长度和距离的定义,并给出了几何相的拓扑原理。最后,计算了谐振子的任意演化几何相。
1 薛定谔演化过程中的几何相
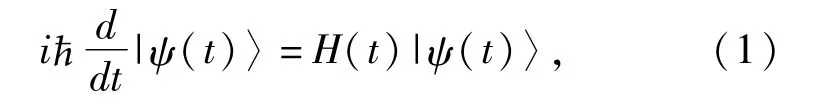
设{ψ}是希尔伯特空间 Q中的一组矢量,且
其中,H(t)为系统的哈密顿量。对于从 t=0到t=t的演化,根据最小 -标准距离函数[5],周期演化满足D2(ψ(0),ψ(t))=[2-21〈ψ(0)|ψ(t)〉|]=0,而非周期演化则满足 D(ψ(0),ψ(t))>0。利用Panchararnam[12]联络,当系统从初态 ψ0=ψ(0)演化到终态 ψ=ψ(t)且两态之间不正交时,两态之间的相对相位差为
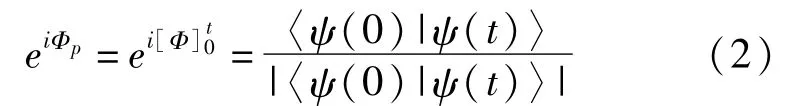
一般地,对于初末态的点之间为非闭合路径时,(2)式给出了经历任意演化[0,t]的量子系统所获得的总相位。于是总相位为
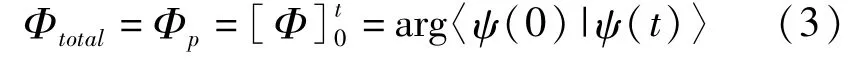
同样可以将总相位表示为
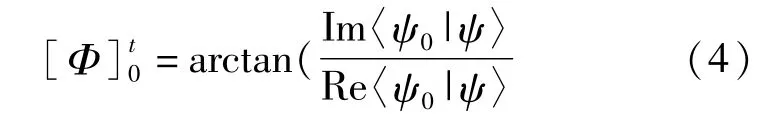
其中〈ψ0|ψ〉=Re〈ψ0|ψ〉+i Im〈ψ0|ψ〉。可见,总相位与R=|〈ψ(0)|ψ(t)〉|的变化不灵敏。
对于任意的量子演化过程,几何相是总相位与动力学相之差(其中动力学相为哈密顿量的期望值)。文献[10]将几何相表示为
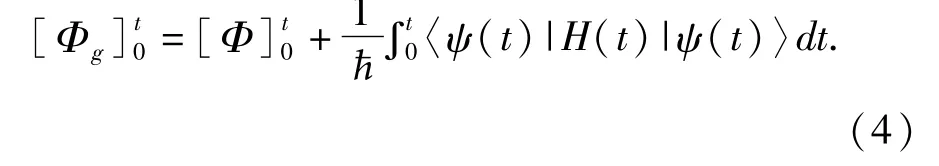
从(4)式可见,要知道几何相还必须知道系统的哈密顿量。
2 几何相位与参考项
设 Γ为闭合积分[0,t]⊂R投影到 l空间的一条闭合曲线,而(d/dt)|ψ(t)〉是曲线 Γ在点 |ψ(t)〉的正切矢量。该正切矢量可以看作被分解为分别属于竖直分量空间 V|ψ〉l和水平分量空间 H|ψ〉l中的两个分量之和。因此,如果空间 P中曲线上一点|ψ(t)〉的投影是个常数,则该曲线被称为是竖直曲线,且竖直曲线的正切称为竖直矢量。相应地,在那点垂直于纤的矢量叫做水平矢量。在 l中给定点的水平矢量集称为那个点的水平空间。为了得到几何相位,有必要给出联络的定义。在主纤丛U(1)→l→P中的联络是正切空间 T|ψ〉l中子空间 H|ψ〉l中的每点|ψ(t)〉的光滑赋值。由此可得,所有的点|ψ(t)〉满足 T|ψ〉l=V|ψ〉l⊕H|ψ〉l,且对于 c∈U(1)有(H|ψ〉l)=Hc|ψ〉l,其中cc*=1,而 δc(|ψ〉)=c| ψ〉表示相位 c对l的诱导行为。
借助于联络的定义,现在来描述纤丛中某矢量的平行输运。将开曲线的水平抬高作为曲线∶[0,t],t→|ψ(t)〉。曲线 Γ是水平的,即vert[Γ]=0,由此在任一时刻 t有,且一般也是开曲线。因此,
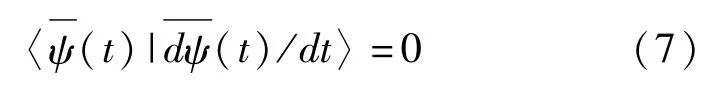
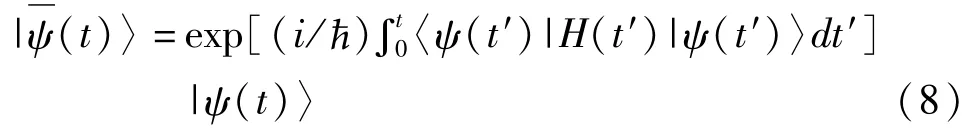
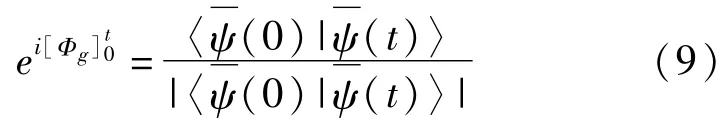
如果将空间 P中的开路径抬高到空间l,那么空间l中会有许多开路径。但是这些路径中会有一个特殊曲线,这条曲线由一个“参考态”描出。定义参考态与初始态矢量〉有关,借助于这个“参考态”将可以定义量子系统的非周期演化几何相。在第IV部分将看到几何相是由水平曲线长度与特殊曲线(非水平)长度不相等所导致的。
为了定义这条特殊的曲线,考虑覆盖 ρ(t)=Π(|ψ(t)〉纤丛的“参考项”|x0(t)〉。这是一个投影过程s∶l→P,各点 ρ(t)∈P的像点在过 ρ的纤Π(ρ)上,也即 Π。s=idp。如果定义与初始点有关的“参考项”为经过s项的态曲线的投影,那么该投影为
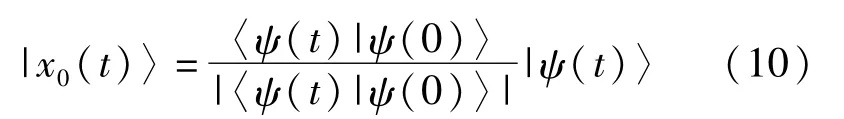
或
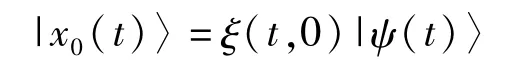
上式中中|x0(t)的下标 0指的是|x0(t)〉总是与初始态|ψ(0)〉有关。如果将初始态表示为 |ψ1(t)〉,那么“参考项”将被表示为 |xt1(t)〉。“|x0(t)〉”是纤丛l的“局域项”,即s:Uα⊂P→l,其中Uα是 P的开领域,且具有以下性质:
(1)sΠ(|ψ(0)〉)=|ψ(0)〉=|x0(0)〉
(2)Π(|x0(t)〉)=Π(|ψ(t)〉)
(3)在量子系统的整个演化过程中〈x0(0)|x0(t)〉始终是正实数。
下面用覆盖投影空间 P中的曲线Γ的“参考项”来定义几何相。对(10)式微分得
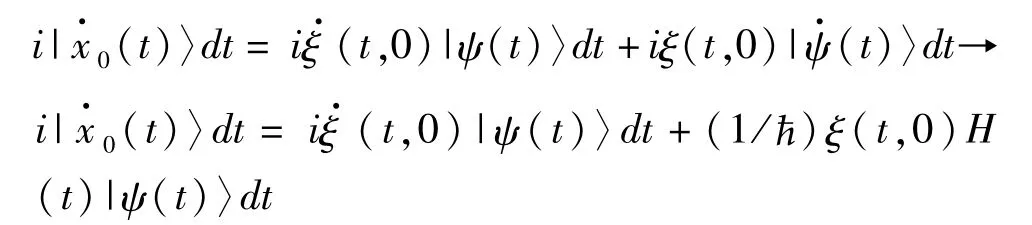
其中·表示对t的微分,给上式左乘〈x0(t)〉|,得
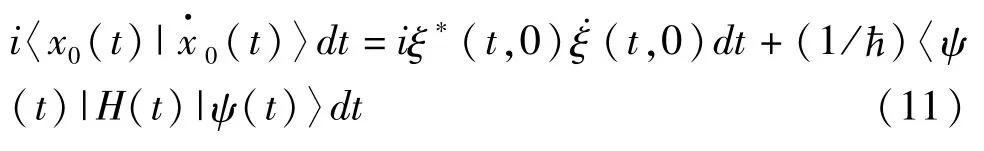
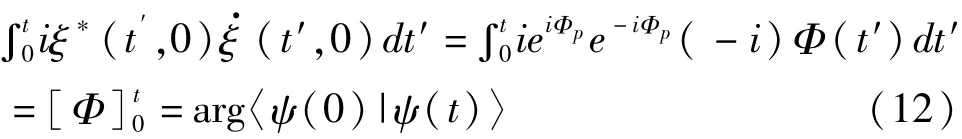
将(11)式两边同时积分,并利用(4)式可得任意量子演化过程中的几何相定义为
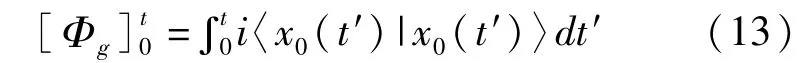
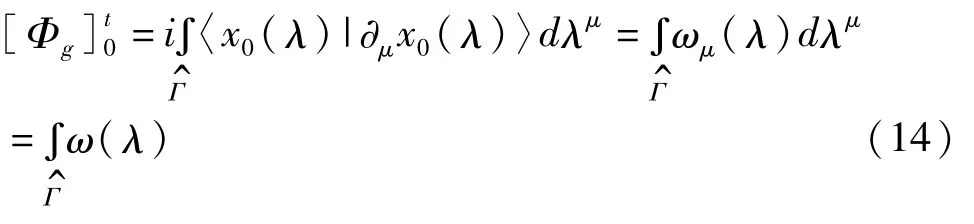
另外,还可以将(13)式表示为对联络一形式的的线积分:其中 ∂μ=∂/∂λμ,λ是希尔伯特空间投影空间P中的坐标。是空间P中连接初始点 Π(|ψ0〉和终点 Π(|ψ〉)的一条曲线。ωμ(λ)=〈x0(λ)|∂μx0(λ)〉是联络形式,它的线性积分给出了几何相。下面将说明非周期几何相的测量不变性。用纤维丛语言来说,测量变换是指从一个局域项(s:Uα⊂P→l)到另一个局域项(s′:U′α⊂P→l)的投影。该投影是投影空间P中两个不同坐标邻域之间交叉的结果。另一种局域项的选择指:作改变|x0(t)〉→|x0(t)′〉=eiη(t)|x0(t)〉,项的改变由结构组 U(1)作用于纤维给出。在这样的测量变换下,联络一形式 ωμ(λ)变换为
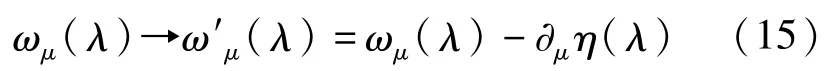
局域项|x0(t)〉将空间P中的一条开路径投影到l中的一条开路径,由此,路径上的初始点和终点是同相的(利用局域项的性质(3))。上述测量变换给出l中的一条不同的开路径为了使|x0(t)′〉成为一个局域参考项,必须要求路径满足局域项的性质(3),即〈x0(0)′|x0(t)′〉始终是正实数。这就要求测量函数必须满足 η(t)=η(0)+2πn。在这样的测量变换下,几何相变为
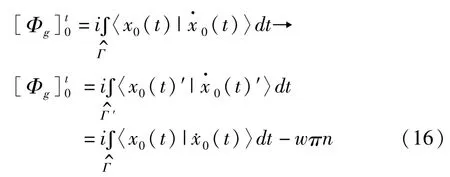
由此可见,用这样的参考项定义的几何相具有测量不变性。几何相定义(13)的重要性在于,即使测地没有闭合初始点和终点,它也有自身的存在性与物理意义。如果测地闭合初始点和终点,那么沿着测地几何相一致为零。下面将利用测地方程和它的解证明这一点。空间 P中的测地定义为具有平稳能量的水平曲线。定义水平曲线的能量为:如果做变量化计算,就会获得水平矢量|
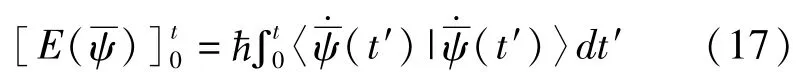
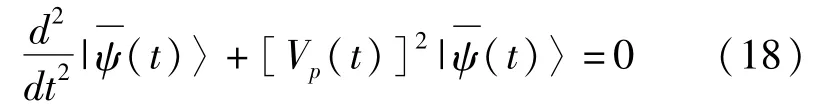
ψ(t)〉满足的测地方程其中Vp(t)=ΔE(t)/ħ是空间 P中态矢的变换速度。这里的 ΔE(t)是系统能量的不确定度。为了简单,假定 ΔE(t)是与时无关的。则测地方程的解为
假定量子系统沿着测地线从 t=0到 t=t演化,那么沿着这条特殊路径的参考项写为
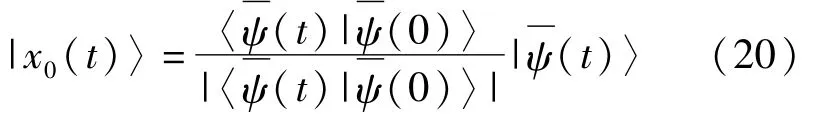
(13)式是一个非定域积分,给出了经过任意的量子演化过程后几何相的开路表达式。动力学相是路径 Γ的定域叠加函数,而几何相是路径的非定域非叠加函数。为了清楚地看到几何相(13)的非叠加性质,量子系统从点 Π(|ψ(t1)〉)到点 Π(|(ψ(t2)〉),然后再从点 Π(|ψ(t2)〉)到点 Π(|(ψ(t3)〉)的演化过程。下面将证明,系统从点 Π(|ψ(t1)〉)到点 Π(|ψ(t3)〉)的演化过程中所获得的几何相不等于从点Π(|ψ(t1)〉)到点Π(|ψ(t2)〉)与从点Π(|ψ(t2)〉)到点Π(|ψ(t3)〉)所获得的几何相之和。系统经过从时刻 t1到 t2,t2到 t3,t1到 t3的演化所获得的几何相分别为参考项|x1(t)和|x2(t)定义为
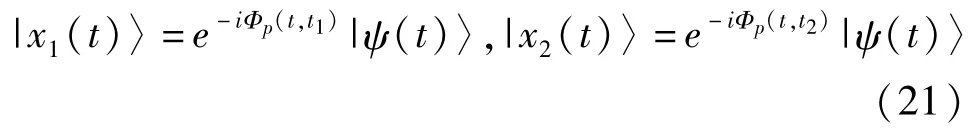
式中 Φp(t,t1)=arg〈ψ(t1)|ψ(t)〉,Φp(t,t2)=arg
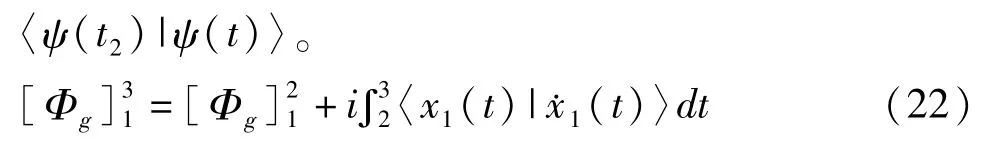
利用(21)式将(22)式表示为
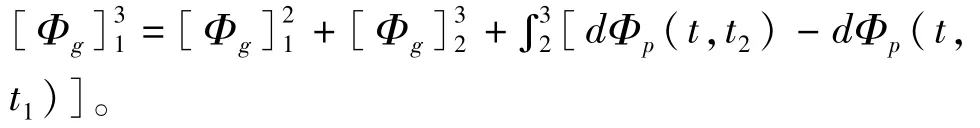
因此,额外的几何相为
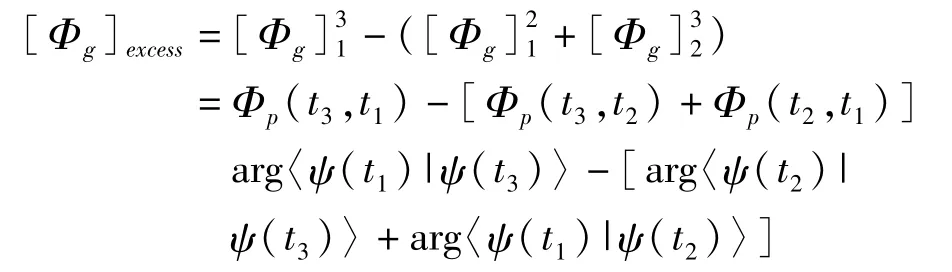
这也和三点的 Bargmann不变有关
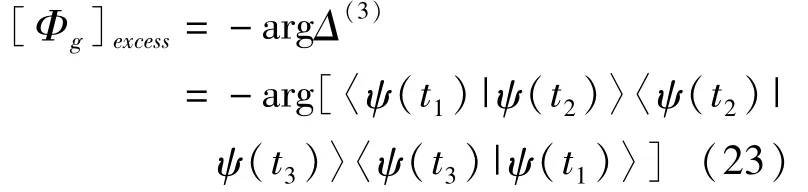
上等式左边仅包含额外的几何相,而右边仅包含额外总相位。这表明额外的动力学相一致为零。这清楚地表明动力学的叠加特性,给出了几何相的非叠加特性。
在适当的极限条件下,几何相(13)退化为绝热Berry相和非绝热A-A相。例如,态矢|ψ(t)〉经过周期演化[0,t]后满足|ψ(T)〉=exp(iΦ)|ψ(0)〉,其中 Φ为总相位。而参考项|x0(t)〉经过周期演化[0,t]后满足|x0(T)〉|x0(0)〉。因此,经历周期演化的量子相位为
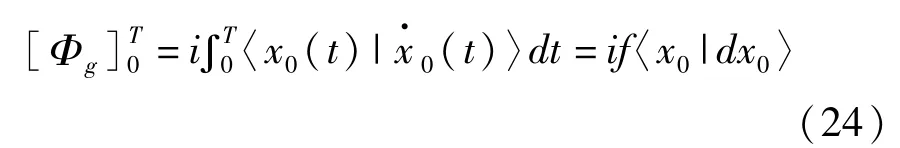
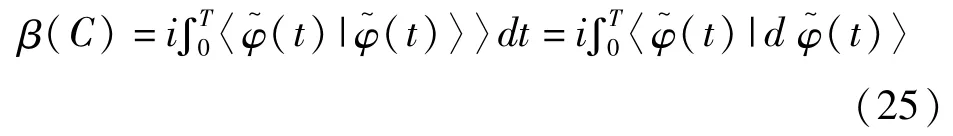
于是,参考项|x0(t)〉和A-A项|φ~(t)〉之间的关系为
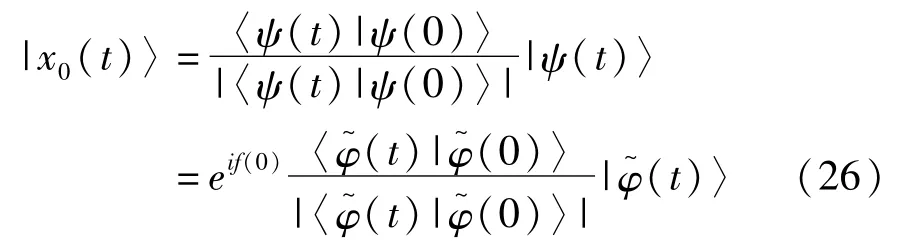
使用(24)将几何相表示为

上式计算时还使用了(12)式。
3 非绝热演化过程中的其它几何结构
这节将寻找任意量子演化过程中的其它几何结构,并探索几何相产生的拓扑原理。描述多体拓扑学的基本几何结构有“长度元”和“距离元”。下面将推导出长度和距离之间的不等式,并证明几何相产生于这个不等式。考虑曲线 Γ0∶[0,t]→l和由参考 项 x0(t)描绘出的曲线:[0,t]→l以及水平曲线(t)〉。我们知道,希尔伯特空间Q中的内积产生一个投影空间P中的度规,而度规定义了空间l中的一条可微曲线的长度。
在量子系统任意的演化过程中使得 t→|x0(t)〉对应于曲线Γ0(t)。那么,可微曲线Γ0从一点 |x0(0)〉到另一点|x0(t)的总长度定义为
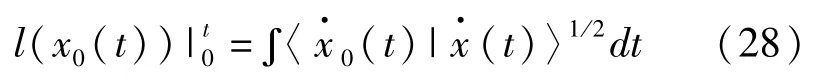
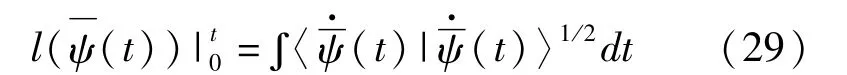
可以证实,(28)和(29)两式所表示的长度的定义也是与任何量子演化过程相关的几何结构。积分(28)和(29)式存在于时间段[0,t]中,且是连续的,积分中所用的参量都是实数。这两个长度都有一个重要的特征—再参量化不变性,即经过做变换 t→t′且>0,由 Γ和得到的所有曲线的长度不变。′因此,曲线的长度与它们投影的参量化无关,是几何曲线的特点,是对 t不变的。而且,这些长度在相位变换下,即|ψ(t)〉→eia(t)|ψ(t)〉,l(x0(t))和l(t))仍然不变。此外,长度与驱动量子系统沿着空间 P路径演化的某个哈密顿量也无关。
除过这些共有的几何特征以外,上面定义的两个长度在本质上是不同的。l(x0(t))在本质上是非叠加的,因为假如量子系统从 t1到t2,然后再从 t2到 t3,t1到 t3的曲线长度不等于从 t1到 t2与 t2到 t3的长度之和。这长度与几何相的特点类似,即不可积性。事实上,长度等于态矢量沿着希尔伯特空间 P中一条曲线的总距离,该距离由 Fubini-Study度规测量得到。希尔伯特空间 P允许 Fubini-Study度规的存在,总距离等于系统经历任意演化过程后能量不确定度的时间积分,即而且,这两个长度是完全不同的几何体。可以看出,曲线长度 l(x0(t))大于曲线长度。为了清楚这一点,计算曲线长度l(x0(t))的无限小量的平方:
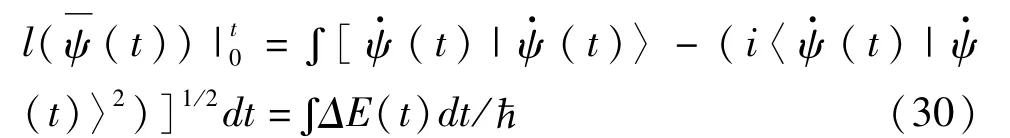
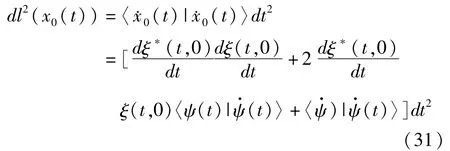
通过计算得,
上式表明,参考项曲线的微小改变与水平曲线的微小改变以及几何相的微小改变构成了正三角,且它们对应的长度,距离和几何相满足勾股定理。
4 2个例子
下面以一些简单例子来说明上文介绍的观点。首先考虑关于二能级原子的简单例子,该模型与自旋1/2粒子与磁场相互作用的模型一致。这里,希尔伯特空间Q=C2,且投影空间 P=P1(C)是个二维球面 S2。在任意时刻t态矢表示为
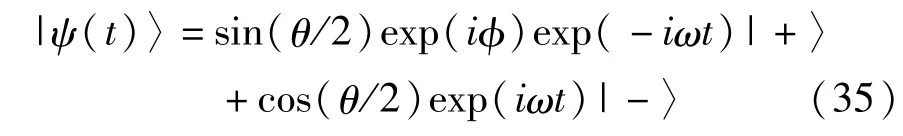
式中,θ和φ是与二能级系统有关的物理参量。基矢|+〉和|-〉是希尔伯特空间中的正交矢量。在非周期演化过程中,态矢以极角 θ和方位角 φ=2ωt的椎体上描绘出一段弧形。假定在自旋演化过程中θ为常数,φ仅随时间而变。参考项|x0(t)〉表示为
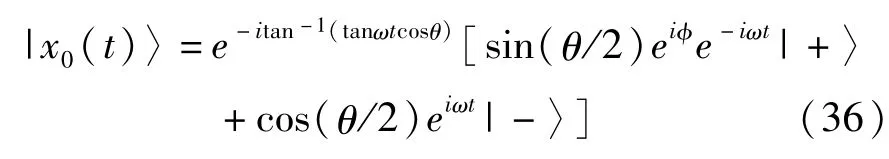
容易看出,该参考项满足第III部分提到的所有特点。使用这个参考项可以计算出二能级原子的非周期几何相为
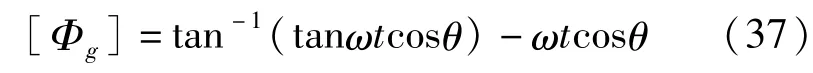
这是一个变化的几何相,相对于线性变化的动力学相,它是非线性变化的。这样的非周期几何相的正确测量已被Wagh和 Rakhecha提出来了。
下面以一维谐振子为例说明以上观点。谐振子的态矢属于希尔伯特空间,谐振子的一维哈密顿量为
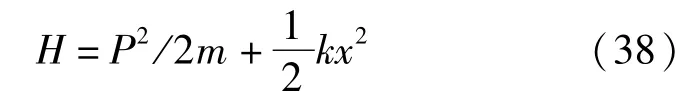
任意时刻 t的态矢用基矢|n〉展开为
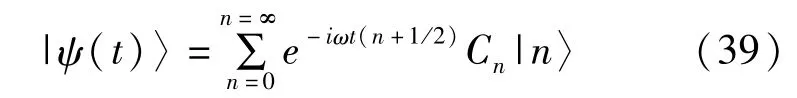
其中展开系数Cn取决于初始态|ψ(0)〉的选取。如果初始态是一个相干态,那么|ψ(t)〉变为
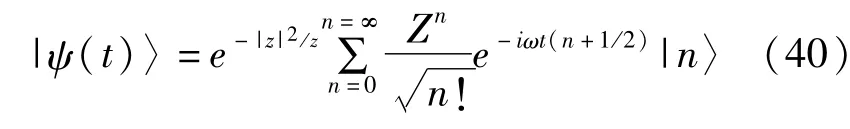
其中Z是复数。归一化的参考项|x0(t)〉与初始态同相,投影到空间P中同一条曲线上,且表示为|x0(t)〉=exp[-|z|2/2+i tan-1
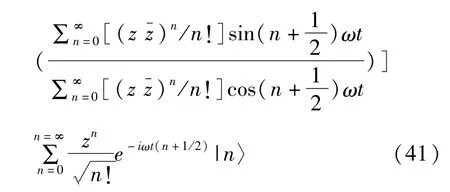
利用参考项|x0(t)〉计算几何相为
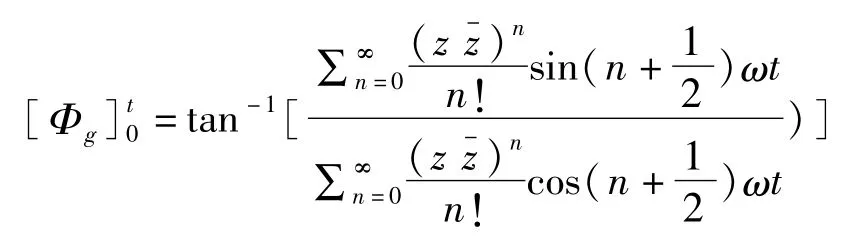

5 结论
本文主要研究了在任意量子演化过程中的几何结构。指出了所有这些几何量之间的关系。利用投影希尔伯特空间 P中线束定义了参考项,并证明通过联络一形式的线性积分给出了几何相表示。指出了几何相的各种特征;证明了几何相不仅是相位不变的,而且是测量不变的;还证明了几何相的消失特性。另外,引入了任意量子演化的几何长度和距离的定义,并给出了几何相的拓扑原理。最后,计算了谐振子的任意演化几何相。
[1]Berry M V.Quantal phase factors accompanying adiabatic changes[J].Proc R Soc A,1984,392:45-57.
[2]Aharonov Y,Anandan J.Phase changes during a cyclic quantum evolution[J].Phys Rev Lett,1987,58:1593-1596.
[3]Zanardi P.RasettiM.Holonomic quantum computation[J]. Phys Lett A,1999,264:94-98.
[4]Pachos J,Zanardi P,Rasetti M.Non-abelian berry connections for quantum computation[J].Phys Rev A,2000,61:010305(R).
[5]Pachos J,Chountasis S.Optical holonomic quantum computer[J].Phys Rev A,2000,62:052318-052323.
[6]Duan L M,Cirac J I,Zoller P.Geometric manipulation of trapped ions for quantum computation[J].Science,2001,192:1695-1697.
[7]Recati A,Calarco T,Zanardi P,et al.Holonomic quantum computation with neutral atoms[J].Phys Rev A,2002,66:032309-032313.
[8]Faoro L,Siewert J,Fazio R.Non-Abelian Holonomies,Charge Pumping,and Quantum Computation with Josephson Junctions[J].Phys Rev Lett,2003,90(2):028301-028304.
[9]Solinas P,Zanardi P,Zanghi N,et al.Semiconductor-based geometrical quantum gates[J].Phys Rev B,2003,67:121307.
[10]Zanardi Pe.Remote state preparation[J].Rev Lett.,2001,87:077901-077905.
[11]Marzlin K P,Bartlett S D,Sanders B C.Entanglement gauge and the non-Abelian geometric phase with two photonic qubits[J],Phys Rev A,2003,67(2):022316-022319.
[12]Li Y,Zhang P,Zanardi P,et al.Non-Abelian geometric quantum memory with atomic ensemblePhys[J].Rev A,2004,70:032330-032334.
[13]Nordling M,Sjöqvist E.Mixed-state non-Abelian holonomy for subsystems[J].Phys Rev A,2005,71(1):012110.
[14]Samuel J,Bhandari R.General setting for Berry's phase[J].Phys Rev Lett,1988,60:2339-2342.
[15]Aitchison I JR,Wanelik K.On the real and complex geometric phaseds[J].Proc R Soc London,Ser A,1992,439:25-34.
[16]Mukunda N,Simon R.Quantum kinematic approach to the geometric phase I.General formalism[J].Ann Phys,1993,228:205-268.
[责任编辑 贺小林]
Geometric Phase Characteristic During Arbitrary Quantum Evolution
WANG PENG1,JIA Pei-jun2
(1.College of Physics and Electrionic Information,Yan an University;2.Assets and Laboratory Management of Yan an University,Yan an 716000,China)
The expression for the geometric phasewas present during arbitrary quantum evolution.The gauge invariant and vanishing property of the geometric phase was showed.Not only the geometric phase was observed,The other geometric structure was found,such as geometric length and distance.The relation among these geometric structure was pointed ont.
geometric phase;quantum evolution;geometric structure
O413
A
1004-602X(2011)01-0023-06
2011 -01 -07
王鹏(1983—),男,陕西吴起人,延安大学助教。

