GEL方法在一维双界面问题中的应用*

姚 阳

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理国防科技重点实验室，四川绵阳621900)

将两种不同坐标系下的计算格式耦合起来的Euler-Lagrange耦合计算方法，在许多计算性学科领域中应用前景非常广阔。例如在爆炸力学问题的数值计算中，往往希望在整体计算区域中流体或大变形的部分，采用Euler方法计算，而对小变形以及固体材料的部分，采用Lagrange方法计算，以能够对整体计算区域的不同区域部分获得更细致的描述，如水下爆炸对船体的影响、低速侵彻问题和一些爆轰驱动问题等。对于这两种不同计算格式，怎样用合理有效的耦合方式、简单的逻辑过程以及不对计算存贮方面有较高限制的Euler-Lagrange耦合方法，已越来越成为关注的热点。

本文中，对一种较新的Euler-Lagrange耦合方法进行研究，它能够自由地对标准Euler和Lagrange计算程序包进行连接，并且不必对他们进行任何实质上的改动，连接过程简单易行［1］。这种方法由R.P.Fedkiw［2］提出，并用于多介质流问题的计算。对于Euler方法面对因运动界面而出现混合网格的难题，利用ghost fluid method(GFM)［3］的思想进行处理。E.Morano等［1］用这种方法进行了在流固耦合方面的研究，并称为 ghost-fluid Euler-Lagrange(GEL)方法。相对 CEL［4］、PISCES［5］、PELE［6］等 Euler-Lagrange方法，GEL对自由边界的处理过程和程序的编制简单、计算量小。

在处理混合网格时，为得到ghost网格上的质量、动量和能量，需要将外插量从Euler真实域穿过界面延拓到ghost域。鉴于在有激波和具有固体不可穿透性质的界面相互作用的数值模拟中，如果选择外插温度或密度，在界面附近往往会出现所谓的overheating误差。为削弱此误差，用isobaric修正变量，即熵、T'(ρ)、e'(ρ)作为第3个外插量将减小这种误差［7］。进一步用isobaric修正技术不仅将外插量向ghost区域延拓，而且还向紧邻界面的Euler真实点延拓，可将误差进一步减小。本文中，扩展了原自行编制的二维GEL程序［8］，将程序用于处理双界面问题以及材料在激波作用下的变形。通过一维黎曼问题，计算当初始间断形成的左右行进激波相遇后，反射波分别穿过界面传播的情况，并通过对isobaric修正方法的具体应用，有效地减小overheating现象。

1 基本方程

1.1 Euler方程

理想可压缩流体Euler控制方程是

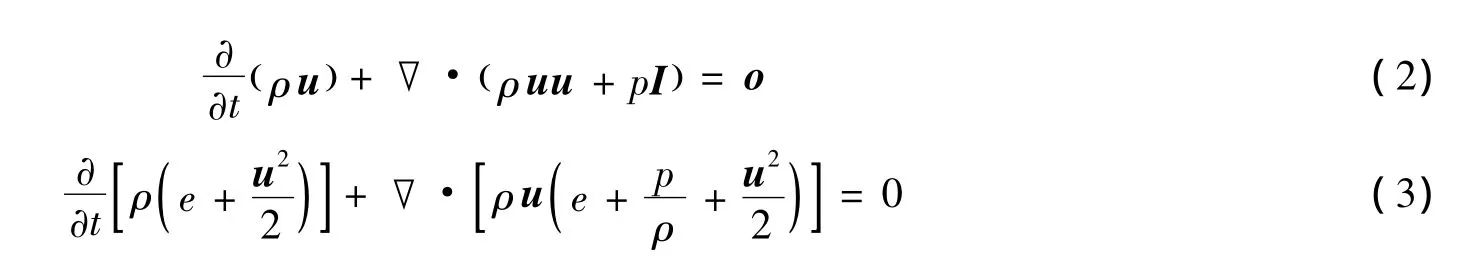
式中:ρ为密度，u为速度矢量，p为压力，e为质量内能，t为时间，I是单位矩阵。状态方程形式取为

Euler计算采用二阶SCB格式［9］编制的计算程序。

1.2 Lagrange方程

连续介质力学给出的基本方程有

式中:ρ、u和E分别表示质点密度、速度和体积内能，~b为体积体力，~σ为Cauchy应力张量。当采用流体弹塑性本构模型时，应力张量分解为

Lagrange计算采用DEFEL二维动力有限元程序［10］。

2 GEL方法

GEL方法中，计算区域中的Euler域和Lagrange域有各自生成的Euler固定网格和Lagrange随体网格。两个区域的交界面称为Euler-Lagrange界面(E-L界面)。E-L界面将整个流场分为Euler和Lagrange域，而且被两个区域共同享有。因为Lagrange节点以随体的速度运动，因此，界面的几何特性可以由Lagrange计算结果确定［2］。由于运动界面的关系，部分的Euler网格被Lagrange网格覆盖，这些被覆盖的Euler网格就是ghost网格，也称为ghost域。因此界面将Euler域分为两个部分:一部分是未被覆盖的真实Euler域，另一部分是ghost域。

与GFM方法相同的是，ghost域上物理量定义点称为ghost点，对物理量的定义可看作是对Euler域内边界物理量的确定。

GEL耦合是根据E-L界面接触间断的性质，界面两侧应满足的物理量条件，在两个计算区域分别确定界面上连续或间断物理量的过程中，内边界条件的确定。对E-L界面上的切向速度、密度(或熵)，在界面两边区域上的这些间断量互不相关，因此两个计算区域分别由各自区域计算结果确定E-L界面上的值。而由界面两侧法向速度的连续性，ghost点的法向速度由Lagrange计算的E-L界面上的法向速度确定，即相当于对Euler域施加了速度边界条件。利用压力是连续量，以E-L界面附近Euler网格的压力，在E-L界面可对Lagrange域施加压力边界条件。通过相互施加边界条件，体现着Euler域和Lagrange域之间的相互作用。图1是E-L界面连续量确定示意图。耦合的过程需在每一时间步计算前进行，然后以统一的时间步长用标准的Euler和Lagrange计算程序分别进行独立地计算。

图1 E-L界面连续量的确定Fig.1 The definition of the continuous quantity in E-L interface

2.1 Ghost域的定义

首先通过程函数

从未被Lagrange域覆盖的真实Euler域，外插压力、熵或密度、以及速度到ghost域。式中:I表示外插量，n是Level set距离函数Φ梯度方向上的单位矢量。Level set函数是点到界面的距离函数。每一时间步，由Lagrange计算的E-L界面，都需重新建立Φ。采用文献［2］中介绍的方法判别Φ的符号。在E-L界面上，Φ=0，n的方向从Euler域指向Lagrange域。

Ghost点的速度的切向分量来自外插速度的切向分量，法向分量还需由Lagrange计算的E-L界面上点的法向速度确定。以二维情况为例，此E-L界面上的点应是距ghost点最近的E-L界面线段上的点，速度值通过此点所在的界面线段两节点的速度值线性内插得到［1-2］。最后，ghost点的速度vG可由一定外插形式的速度合成公式计算。采用反射外插公式［1-2］

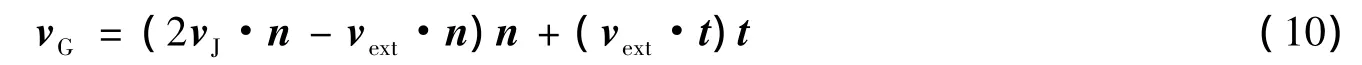
式中:vJ表示距ghost点最近的E-L界面上点的速度，vext表示外插的速度，t为垂直于n的单位矢量。式(10)反映了界面的不可穿透性［1］。

2.2 Isobaric修正技术

除压力和速度外，还需要得到ghost网格上第3个独立的物理量。因为在有激波和具有固体不可穿透性质的界面相互作用的数值模拟中，界面附近往往会出现所谓的overheating误差，而压力和速度在界面保持一致。为削弱此误差，除了用isobaric修正变量，即熵、T'(ρ)和e'(ρ)作为第3个外插量外，还可以用isobaric修正技术将误差最小化［7］。在GEL方法中，外插时凡是满足

所有Euler域格点的物理量也随之改变。式中:Δx为网格宽，k为无物理意义的非零常系数，可根据数值模拟结果调整具体值。采用isobaric修正技术后，对需要进行速度合成的点也相应地扩大范围。

2.3 Lagrange域压力边界条件的确定

对Lagrange域的计算来说，在E-L界面上施加压力边界条件，体现来自Euler域的作用。GEL中，这实际上是对于组成E-L界面上每条线段(二维情况下)的两个节点，受到的来自Euler域压力值的确定。文献［1-2］中由内插得到线段中点受到的压力值，作为整条线段受到的平均压力值。而本文中分别计算了界面线段跨越的所有Euler网格对线段各部分施加的压力值，将这些压力值累加后再平均分配给线段的两个端点，即［8］

式中:m为每条E-L界面线段跨越的Euler网格数总和，pj为Euler网格的压力，lj是线段在Euler网格中的长度。

2.4 统一计算时间步长

时间步长［2］

式中:0.5为CFL系数，ΔtE和ΔtL分别是Euler和Lagrange计算得出的时间步长。最后，Euler域和Lagrange域均以此步长分别进行独立地计算。

2.5 多界面的处理

GEL对两种计算格式在界面的处理，对Euler计算来说，实际上就是对ghost域上各物理量的定义;而对Lagrange计算，是E-L界面上节点压力边界条件的计算。这些耦合的过程相对于他们各自的计算，是完全独立的，因此在多界面问题中，界面与界面的处理过程，或者说每一个在界面上发生的Euler和Lagrange耦合过程是相互独立的。因此，GEL扩展到多界面问题是完全直接的。

3 数值算例

考虑一维理想气体和水的黎曼问题，计算区域为［0 m，3 m］。流场左右边界均为流动边界，左边流场和右边均为初始是静止状态的高压双原子理想气体，压力p=7.81 GPa，密度ρ=0.6 g/cm3，多方指数γ=1.4，这两部分的计算采用以SCB格式编制的计算程序。流场中间为水，初始也是静止状态，密度ρ=1 g/cm3，压力 p=0.1 MPa，此部分流场的计算采用 DEFEL二维动力有限元程序，状态方程为Grüneisen状态方程。初始左右两界面分别在x=0.5，2.5 m处。左右两边流场的网格数为100，而中间部分为400，以本文中GEL耦合程序进行耦合。

图2是不进行isobaric修正时的密度、速度和压力结果。可以看到:当t=0.16 ms时，左右两方向的激波传至Lagrange域，但未相遇;当t=0.32 ms时，两激波已经过碰撞后进行反射;当t=0.43 ms时，两激波穿过界面到达左右两边的Euler域。从3个计算时间的结果看，只有当t=0.43 ms时左右界面处均出现明显的overheating现象，尤其压力较为明显，引起的相对误差为约8.6%。

取isobaric修正值Φ≥－0.36Δx，在t=0.43 ms与不进行修正计算结果的比较见图3，最后为压力图像在左边界面处的放大图。此时overheating现象有效减小，引起的相对误差为约2.6%。

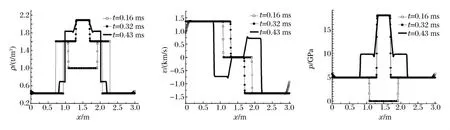
图2 无isobaric修正时的结果Fig.2 The results with no isobaric fix technique

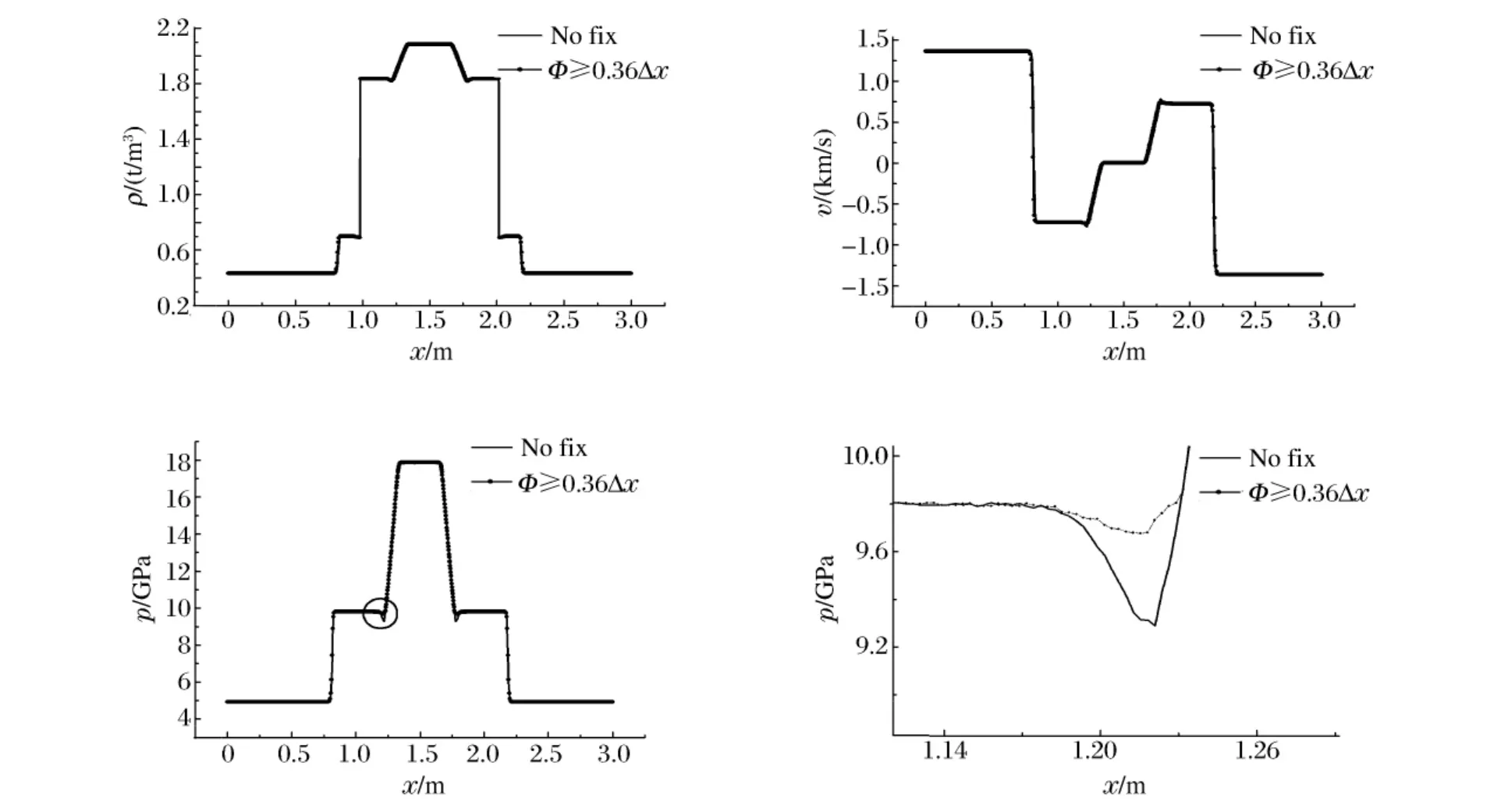
图3 Isobaric修正后与无isobaric修正时的结果比较(t=0.43 ms)Fig.3 The resultswith isobaric fix technique are compared against the one with no fix in t=0.43 ms

4 讨论

GEL方法从理论和计算上将整个计算流域分为Euler和Lagrange域，结合Euler和Lagrange两种计算方法的优越性;处理混合网格借助ghost-fluid的思想，程序编制相对简单，计算量小;在耦合过程中，对每一界面的处理是独立的，因此扩展到双界面甚至多界面问题是完全直接的。本文中GEL耦合程序中，对Lagrange域在界面上施加压力边界条件的方法和以往文献给出的方法不同。模拟了双界面一维理想气体和水的Riemann问题，以及有机玻璃圆柱在冲击波作用下变形的二维问题。

从一维黎曼问题算例计算结果看到，当计算时间为0.43 ms时，即波阵面从Lagrange域穿过界面传播到Euler域时，界面处overheating现象明显比前两时刻增大，而取其他一些isobaric修正量进行计算时也出现了相同情况。这是否由于两种计算格式对耦合的不同处理，以及外插方向与波行进方向不一致而造成，仍然需要进行进一步的探讨。

［1］Morano E，ArientiM，Hung P，etal.A level setapproach to Eulerian-Lagrangian coupling［J］.Journal of Computational Physics，2003，185:213-251.

［2］Fedkiw R P.Coupling an Eulerian fluid calculation to a Lagrangian solid calculation with the Ghost fluid method［J］.Journal of Computational Physics，2002，175:200-224.

［3］Fedkiw R，Aslam T，Merriman B，et al.A non-oscillatory Eulerian approach to interfaces in multimaterial flows(The Ghost fluid method)［J］.Journal of Computational Physics，1999，152:457-492.

［4］Noh W.CEL:A time-dependent，two space dimensional，coupled Eulerian-Lagrangian code［C］∥Methods in computational physics.New York:Academic Press，1964:117-179.

［5］Hancock S.PISCES 2DELK theoretical Manual［Z］.Physics International，1985.

［6］McMasterW H.Computercodes for fluid-structure interactions［C］∥Proc 1984 Pressure Vessel and Piping Conference.San Antonio，1984.

［7］Fedkiw R，Marquina A，Merriman B.An osobaric fix for the overheating problem inmultimaterial compressible flows［J］.Journal of Computational Physics，1999，48:545-578.

［8］姚阳，李平，柏劲松，等.Euler-Lagrange耦合计算的 GEL方法［J］.爆炸与冲击，2007，27(5):420-425.YAO Yang，LIPing，BAIJin-song，et al.Euler-Lagrange coupling with GEL［J］.Explosion and Shock Waves，2007，27(5):420-425.

［9］Zhao N.High resolution SCB scheme for hyperbolic systems of2-D conservation laws［J］.Journal of Computational Physics，1998，16(2):179-192.

［10］DEFEL Users Manual［Z］.Dyna East Corporration，1988.