永磁同步电机控制系统控制器参数的优化设计

姜重然， 陈文平， 徐斌山

(佳木斯大学信息电子技术学院，黑龙江佳木斯 154007)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)是多变量、非线性、强耦合的系统，常规PID控制器容易受电机参数变化和负载扰动等不确定因素的影响，对动态响应和抗干扰能力难以兼顾，PMSM矢量控制系统能够实现高精度、高动态性能、大范围的调速或定位控制，因此PMSM矢量控制系统引起了国内外学者的广泛关注。通常在速度控制器中要加入一个饱和函数对输出信号进行限幅，这样，实际被控对象的输入控制信号和控制器的期望输出不等，导致系统的动态响应变差，这种现象被称为 Windup现象［1］，但是通常情况下饱和是必不可少的，它可以使PMSM起动达到“时间最优控制”。PMSM控制系统中的积分环节造成系统的Windup现象，导致系统输出超调增大，稳定时间增长，造成系统的动态特性变差，甚至会引起系统的不稳定。

针对这一问题，需要设计抗饱和策略，既通常所说的Anti-Windup，使系统出现饱和时，尽快退出饱和区。目前大多数的Anti-Windup控制器属于“二步法”设计［2］，即首先不考虑系统的非线性特性，根据线性系统理论设计出满足系统性能指标的线性控制器;然后在该控制器的基础上，加入补偿环节。二步法充分利用线性系统控制理论和设计方法。但是，由于采用了分步设计原则，忽略了非线性环节加入线性控制器对系统闭环相应的影响，改变了系统的闭环性能，难以达到预期的效果［3］。许多学者提出了新型的Anti-Windup控制器来改善系统性能［4-5］，增加了抗饱和量给系统的负反馈输入端，使控制效果更加理想。如果对传统的Anti-Windup控制器的参数进行寻优，得到最优的控制器参数，既提高了系统性能，又减小了计算量。常见的寻优方法有最速下降法、共轭梯度法、牛顿法和单纯形法，其中单纯形法非常适合于非线性控制系统的参数优化问题，采用单纯形法的调节参数自寻优方法具有良好的收敛性。本文将单纯形法应用在Anti-Windup控制中，很好地优化了抗饱和PI控制器的参数，仿真和试验结果表明了单纯形法应用在PMSM的Anti-Windup控制器参数优化，可以很好地改善系统的动态性能。

1 PMSM矢量控制模型

将PMSM在a-b-c三相静止坐标系下的电压方程进行Clark变换，Park变换，得到d-q坐标系下PMSM的定子电压方程为

式中:ud、uq——定子电压 d、q 轴分量;

ψd、ψq——磁链的 d、q 轴分量;

ωe——电角速度。

d-q坐标系下磁链方程为

Ld、Lq——定子绕组 d、q 轴等效电感。

系统的机械运动方程为

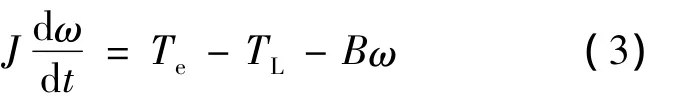
式中:TL——负载转矩;

B——摩擦系数;

自抗扰控制器由韩京清教授提出，由三部分构成：跟踪微分器、扩张状态观测器、非线性状态误差反馈控制律[7-10].自抗扰控制由于对系统模型的依赖程度不高，对系统的自身参数变化以及外部扰动等因素可以精确估计，同时算法易于工程实现[11-13].因此，在工业控制、机器人控制、航空航天等领域获得了广泛的应用.对于单级倒立摆自抗扰控制器设计如下：

ω——电机转子的机械角速度，满足 ω=ωe/pn;

J——系统的转动惯量。

对于面贴式PMSM，其电感满足下列条件:Ld=Lq=L。电机的转矩与d轴电流无关，只与q轴电流成线性关系:

根据式(1)～式(4)，得到面贴式PMSM的状态方程为

式中:θ——电机转子的机械角位置，θ= θe/pn。

PMSM的矢量控制方法很多，其中id=0控制，实现了PMSM的解耦控制，最简单也最常用。该系统采用双闭环控制结构实现id=0矢量控制方式。图1为PMSM矢量控制系统框图。

图1 PMSM矢量控制系统框图

2 电流环Anti-Windup PI控制器设计

由图1可见，在该系统中需要设计三个控制器:速度控制器、d轴电流控制器、q轴电流控制器。由于PMSM的电流给定量需要限幅，所以速度控制器需要加入一个饱和函数，而PI控制器的积分环节会造成Windup现象，执行机构的实际输出与PI控制器的输出不等，若将两者的差值作为反馈信号就可以控制两者的大小差异，抑制Windup现象。传统的Anti-Windup PI控制器如图2所示，PI控制器带输入限幅，把与的差反馈到积分环节，控制器输出表达式为［5］

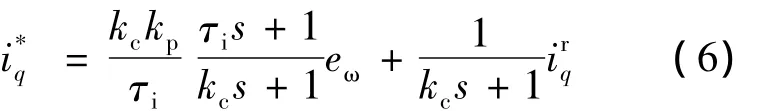
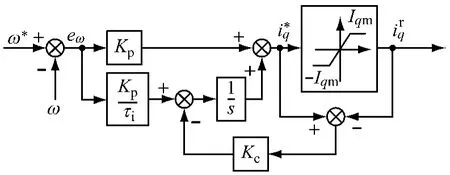
图2 传统的Anti-Windup PI控制器

由于电机的速度存在震荡，相对于电流环，速度环的参数对系统的性能影响大，对参数要求苛刻。因此，速度环的参数整定工作费时费力，由于各种因素的影响，整定效果仍然不够理想。传统的方法是采用“二步法”设计，即先设计PI参数KP、τI，再整定Kc的值，KP为比例项放大倍数，τI为积分常数，Kc为积分项放大倍数。这种将非线性环节引入到线性控制器中对系统的闭环控制没有很好的预见性，达不到很好的控制效果。本文用单纯形法优化速度环的控制参数 KP、τI、Kc的值。

3 单纯形法

单纯形法的基本思想［6］是:在n维空间中取n+1个点构成初始单纯形，比较n+1个点处目标函数值的大小，丢弃最坏的点，代之以新的点，构成新的单纯形，反复迭代，使其顶点处的函数值逐步下降，顶点逐步逼近目标函数的最小点。因为该系统有三个参数KP，τI，Kc需要选择，所以可用三维空间上求目标函数最小值来求得最优解。若要求该函数的极值点，则可先计算四个点处的函数值，进行比较，并根据它们的大小关系确定函数的变化趋势作为搜索的参考方向，然后按参考方向搜索直到找到极值点为止。

4 仿真与试验

PMSM 的参数如下:PN=1.5 kW，nN=1 000 r/min，IN=3.5 A，UN=380 V，pn=3，Rs=2.875 Ω，L=33 mH，J=0.011 kg· m2，B=0.002 N·m·s，ψf=0.8 Wb。交轴电流限幅值Iqm=6 A。

PI控制器采用传统的Anti-reset Windup方法［7-8］整定参数。

PI控制器交轴电流环参数如下:kp2=2，τi2=0.005;直轴电流环参数如下:kp3=20，τi3=2。

PI控制器速度环参数如下:kp1=0.3，τi1=0.058 2;分别使 kc1=0.02 和kc1=0。如图4、图5所示，可看出加入抗饱和可以使控制器更快的退出饱和状态，并且较好地抑制速度的超调。

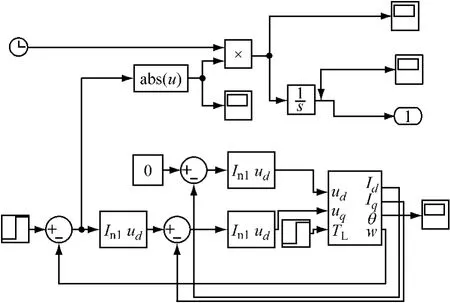
图3 PMSM系统优化模型

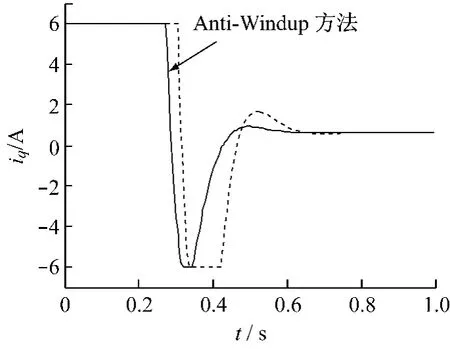
图4 q轴电流变化

图5 PMSM速度曲线

接下来对速度环的三个参数KP，τI，Kc用单纯形法优化，选取的初值如下:kp1=0.3，τi1=0.058 2;kc1=0.02。优化后参数变如下:kp1=1.703 9，τi1=0.021 4;kc1=65.097 7。目标函数变化曲线如图6所示，可看出优化过程中目标函数的值逐渐变小。由图7可看出，优化后电流退出饱和的时间减小了0.2 s。速度变化曲线如图8所示，在0.18 s之前由于电流都处于饱和状态，速度曲线基本相同，在0.18 s之后，优化后的系统退出饱和，可看出优化后速度的超调量明显减小，收敛更快，震荡小。图9、图10分别为优化前后PMSM在起动开始前一秒的三相电流变化曲线，可以看出优化后，电流退出饱和的时间减小了近 0.2 s，控制效果更加理想［9］。

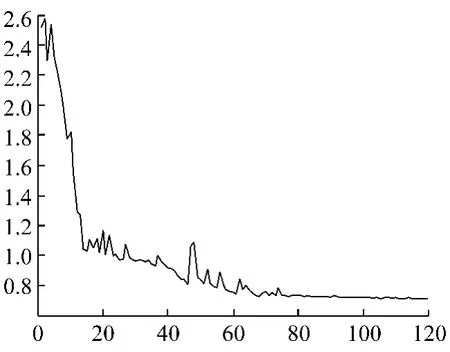
图6 目标函数变化

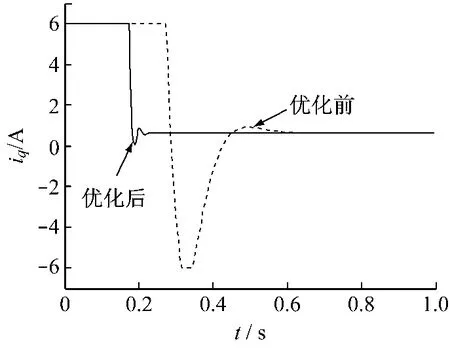
图7 优化前后q轴电流变化

为了验证单纯形法可以很好的优化抗饱和PI控制器的参数，选择不同的初值，得到如图11所示的速度变化的响应曲线，虽然选取不同初值时最终优化出来的参数不同，但控制效果都有较大改善。

图8 优化前后PMSM速度曲线

图9 优化前PMSM三相电流曲线

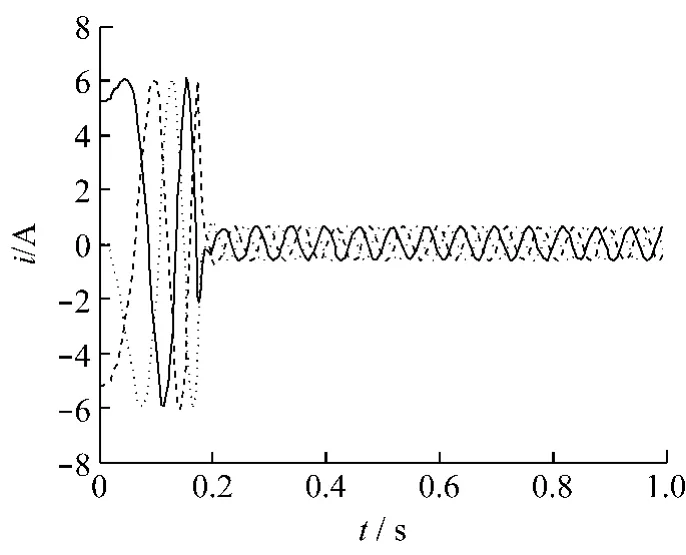
图10 优化后PMSM三相电流曲线

图11 PMSM速度曲线

对优化结果在实验平台上验证，数字信号处理器(Digital Signal Processor，DSP)在线运行控制PMSM，用CCS内部的示波器，测量PMSM实际运行的速度曲线。给定转速n=600 r/min使用初始的Anti-Windup PI控制器参数控制PMSM系统得到实际的速度响应曲线如图12所示;经过单纯形法优化得出的参数应用在实际控制系统速度响应曲线如图13所示。由图可看出经过优化的参数在控制PMSM时超调量变小、响应快，得到的速度曲线更加理想［10］。

图12 优化前PMSM速度曲线

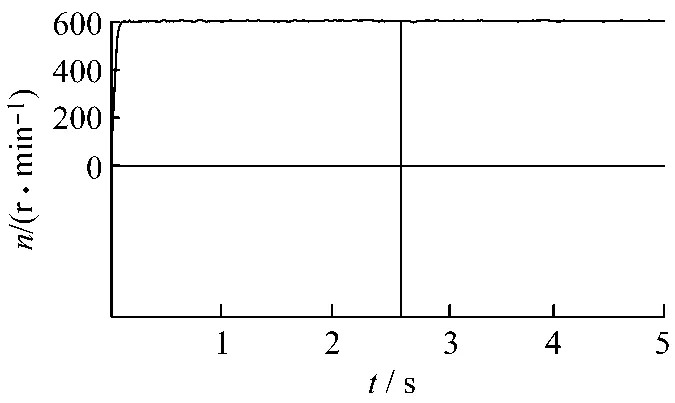
图13 优化后PMSM速度曲线

5 结 语

本文对PMSM的矢量控制系统进行分析，使用MATLAB中的fminsearch函数(单纯形法)优化了速度环的抗饱和PI控制器的参数KP，τI，Kc的值，克服了传统Anti-Windup控制器二步法参数整定的缺点，使控制系统的动态性能得到很大的提高。仿真和试验的结果证实经过优化后的系统响应速度快、超调量小，验证了所介绍方法的有效性。

［1］Peng Y， Vrancic D， Hanus R. Anti-windup，bumpless，and conditioned transfer techniques for PID controllers［J］.IEEE Control Systems Magazine，1996，16(4):48-57.

［2］Kothare M V，Campo P J，Morari M，et al.A unified framework for the study of Anti-Windup designs［J］.Automatica，1994，30(2):1869-1883.

［3］Park J K，Choi C H.Dynamic compensation method for multivariable control systems with saturating actuators［J］.IEEE Trans on Automation Control，1995，40(9):1635-1640.

［4］Bruckner M.Optimal model based Anti-Windup design［C］∥IEEE International Conference，2008(9):3-5.

［5］Grimm G，Teel A R，Zaccarian L.Robust linear anti-windup synthesis for recovery of unconstrained performance［J］.International Journal of Control，2004:36.

［6］寇宝泉，程树康.交流伺服系统及其控制［M］.北京:机械工业出版社，2008.

［7］杨承志.参数寻优智能PID控制［J］.昆明理工大学学报，1998，23(5):95-99.

［8］David J，Kruglinski.Visual C + + 技术内幕［M］.北京:清华大学出版社，1999.

［9］Shin H B.New antiwindup PI controller for variablespeed motor drives［J］.IEEE Trans on Industrial E-lectronics，1998，45(3):445-450.

［10］杨明，徐殿国，贵献国.永磁交流速度伺服系统抗饱和设计研究［J］.中国电机工程学报，2007，27(15):28-32.