含非贯穿直裂纹管道的振动特性分析

胡家顺，冯 新，周 晶

(1.中国石油集团安全环保技术研究院 安全技术研究所，北京 100083;2.大连理工大学 海岸和近海工程国家重点试验室，大连 116024)

在交变荷载的长期作用下，裂纹的萌生和扩展导致结构抗力衰减，甚至引起结构的破坏和倒塌。近年来，裂纹结构的振动分析、裂纹诊断受到了普遍关注，已成为研究热点之一［1－10］。荷载作用下，结构裂纹尖端附近区域出现应变能集中，引起了局部柔度的变化。Irwin［3］使用等效弹簧的概念从宏观上量化荷载与裂纹尖端应力集中的关系，通过测量裂纹梁局部柔度描述应力强度集中，成为早期试验确定应力强度因子的标准方法，推动了含裂纹结构力学响应分析的发展。上个世纪末，Dimarogonas 和 Papadopoulos 等人［4－6］在裂纹结构局部柔度的计算理论方面做出了重要贡献，其研究成果被广泛应用于土木、机械等行业。

局部柔度系数是裂纹结构振动分析、裂纹识别的基本参数，目前根据局部柔度建立的裂纹模型，绝大多数是基于矩形或圆形的实体结构得到的，例如矩阵或圆形截面的梁类结构、矩形截面的板类结构、圆形截面的杆类结构等。而针对空心圆柱体结构的裂纹模型、振动分析和裂纹识别则鲜有文献报道［7－9］，Liu 等人［7］建立了贯穿裂纹管的裂纹模型，研究了管道轴向、横向振动的特点，利用裂纹管轴向与横向耦合振动特性进行裂纹识别，文中没有考虑剪切力下的局部柔度的作用。Zheng等人［8］分别推导了含横向裂纹的矩形、圆形截面空心柱体在纯弯矩作用下的局部柔度方程，并使用128点高斯积分计算无量纲的局部柔度系数，文中没有考虑轴向、剪力的影响。Naniwadekar等人［9］使用静、动力方法确定了含非贯穿直裂纹的管道在纯弯矩作用下4种裂纹深度的局部柔度系数，但文中没有使用应力强度因子建立裂纹管局部柔度的理论解。

本文根据线性断裂力学理论，推导了非贯穿直裂纹管在轴力、剪力和弯矩联合作用下的局部柔度方程，克服了当前方法仅针对特定的荷载模式或非空心截面的缺陷，采用适应性的Simpson数值积分方法求解得到裂纹管的附加柔度系数，继而建立了裂纹管结构的有限元模型。实例分析了裂纹位置、裂纹程度变化对裂纹管结构自振频率的影响。

1 裂纹管局部柔度系数理论推导

假设管道裂纹为张开型裂纹，即在振动过程中假设结构中裂纹一直处于张开状态。非贯穿直裂纹是管类结构中常见的损伤类型之一，如图1所示。

图1 (a)裂纹管示意图;(b)裂纹管单元;(c)裂纹截面几何尺寸Fig.1 (a)Sketch of pipe with a straight front and part-through crack;(b)Cracked pipe element;(c)Cracked section geometry

非贯穿直裂纹如图1(a)所示，裂纹深度为a，管壁厚为t，管外径为De，管内径为Di。裂纹管单元受到轴力P1、剪力P2和弯矩P3的联合作用。假设P1方向与管轴重合;P2和P3关于裂纹横截面C－C对称，合力F方向见图1(c)。与梁类结构裂纹不同，管类结构非贯穿裂纹区域是一个圆弧形区域，裂纹深度不再是一个恒定的常数，对于此类型裂纹，无法直接获得应力强度因子求解其局部柔度系数。本文根据Dimarogonas［4］建立裂纹转轴局部柔度的思想，把裂纹区域离散为一序列独立的矩形条带，各矩形条带按照裂纹梁理论计算附加应变能，然后积分得到总应变能，从而求得裂纹引入的局部柔度。

根据图1(c)所示的几何关系，得到如下的表达式:

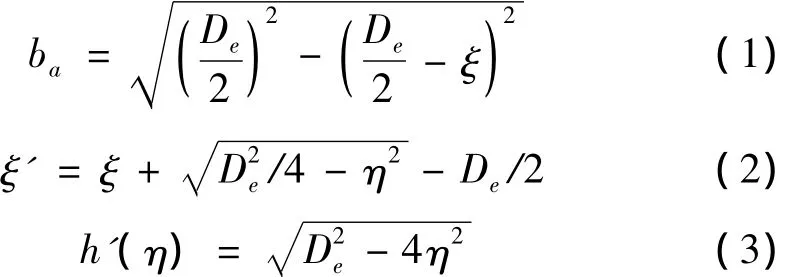
式中:ba表示裂纹深度ξ处水平截面的一半宽度，ξ'为距离积分条带顶部的局部深度变量，h'(η)为积分条带深度，ξ、η分别为全局坐标下的深度变量和偏移距离。

假设在外力作用下，结构中裂纹区域处于弹性阶段，根据线弹性断裂力学理论，裂纹出现所产生的附加应变能［5］表示为:

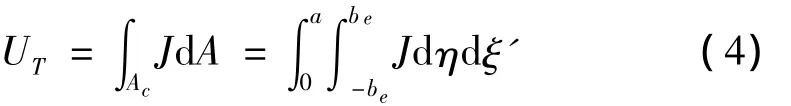
式中:J为应变能释放率，Ac为有效裂纹面积。裂纹引起的附加应变能释放率J可表示为:

式中:KⅠ1、KⅠ2、KⅠ3分别为轴力、剪力、弯矩引起的Ⅰ型裂纹的应力强度因子;为剪力引起的Ⅱ型裂纹的应力强度因子。在平面应力状态下E'=E;在平面应变状态下E'=E/(1－υ2)。其中，E为弹性模量，υ为泊松比。

对于裂纹管，在轴力、剪力和弯矩作用下，各条带裂纹区域应力强度因子可表示为［10］:

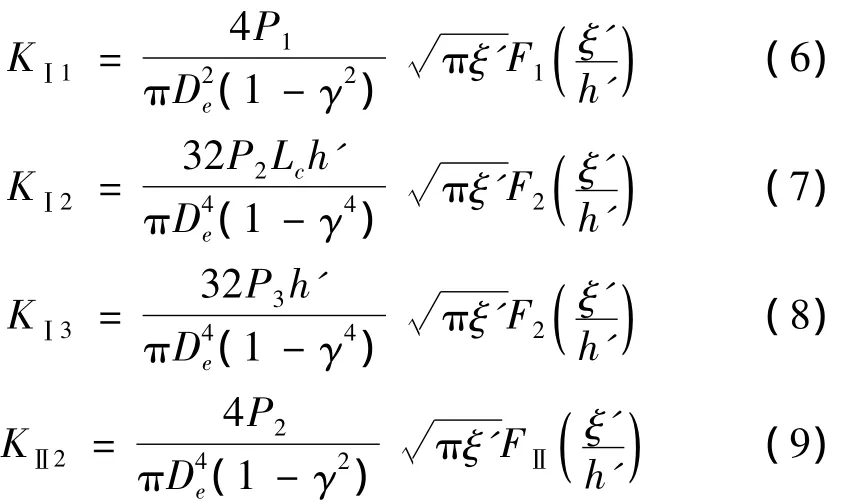
式中:Pi(i=1，2，3)分别表示裂纹单元的轴力、剪力和弯矩，γ=Di/De，F1、F2、FⅡ为应力强度因子的修正系数，可表示为［11］:

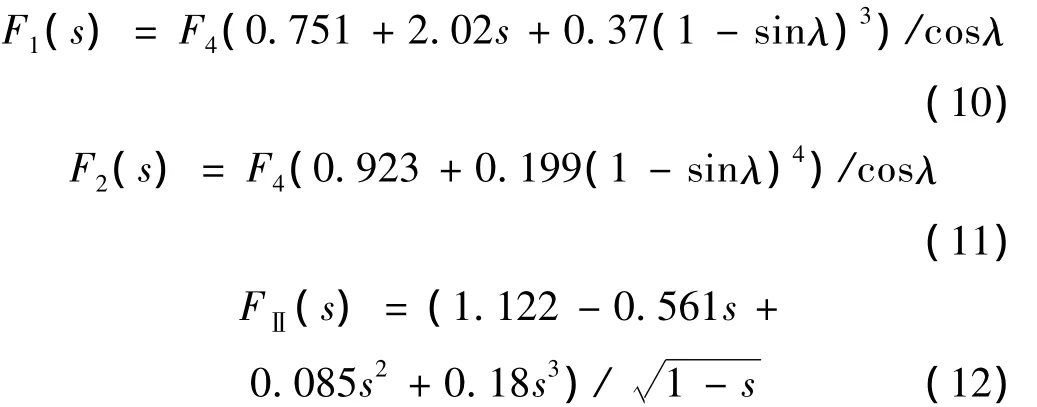
根据卡式定理(Castigliano’s theorem)，裂纹引入的附加位移可表示为应变能对力的导数:

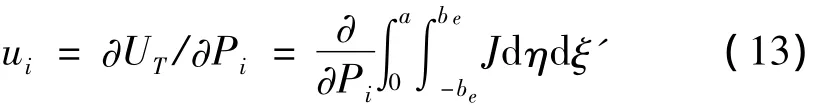
则裂纹引起的附加局部柔度可表示为:

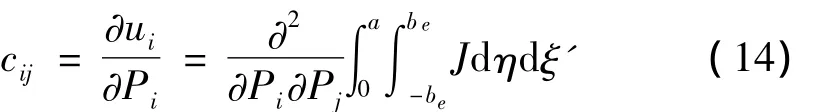
式中:cij(i，j=1，2，3)为各对应荷载引入的裂纹管附加柔度。

转换积分表示方式，设x=ξ/De，y=η/De。

由式(2)、式(3)得:

把式(6)～式(9)代入式(14)，进行无量纲处理，得到非贯穿直裂纹管的无量纲局部柔度系数PTF。为了区别于局部柔度系数cij，下文把无量纲局部柔度系数 PTF简称为“无量纲柔度”。

式(16)～式(19)是关于x，y内积分限为函数的双重积分，且内部积分函数形式复杂，无法直接获得无量纲柔度的解析解。本文采用适应性Simpson数值积分方法编写程序对上述方程进行求解，适应性Simpson算法具有求解速度快，精度高等特性［12］。

2 理论验证

Naniwadekar等人在文献［9］中使用静力和动力的测试方法得到了不同裂纹深度非贯穿直裂纹管在纯弯矩作用下的扭转弹簧刚度。以文献［9］中裂纹管道的试验模型为基准，根据本文方程计算基准模型局部柔度系数的理论解，通过与Naniwadekar等人的试验值对比验证本文局部柔度系数推导和求解的合理性。

文献［9］中静力测试裂纹等效刚度Kt表示为:

式中:M为裂纹截面位置的弯矩，ΔU为裂纹引起的附加应变能。裂纹管在弯矩作用下局部柔度系数c33可表示为等效刚度的倒数:

本文推导的局部柔度系数c33表示为:

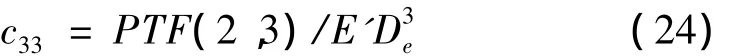
基准模型管的物理参数和裂纹深度如表1所示，基准模型管局部柔度系数c33的计算值与试验值如图2所示。

表1 物理参数和裂纹深度Tab.1 Physical parameters and crack depth

图2 基准模型局部柔度系数的计算值与试验值Fig.2 Calculating results and experimental results of the local flexibility due to a crack

从图2中可以看出:随着裂纹深度的增加，裂纹管局部柔度系数的理论解与试验值都逐渐增大。使用本文理论求解的局部柔度系数与试验测试结果基本吻合，本文的理论解略低于试验值。相对于文献［9］，本文给出了非贯穿直裂纹管在轴力、剪力和弯矩作用下局部柔度系数的理论推导和求解方法，使用该方法可以求解任意裂纹深度非贯穿直裂纹管的各局部柔度系数，避免为了获得局部柔度系数进行的大量试验工作，且求解结果满足工程实际要求。

3 裂纹管有限元模型

求得裂纹管局部柔度系数后，可建立使用扭转弹簧模拟的“弹簧铰”裂纹模型或使用局部柔度矩阵构建的“有限元”裂纹模型。如图1(a)所示裂纹管单元的总体柔度等价于无裂纹单元柔度与裂纹引起局部柔度的代数和［10］

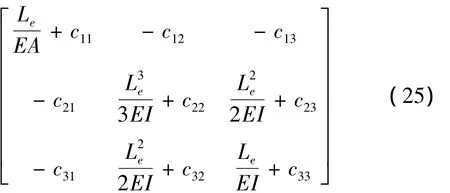
式(25)可进一步表示为含裂纹单元的刚度形式:

其中，转换矩阵T表示为:

裂纹管道的动力特征方程表示为:

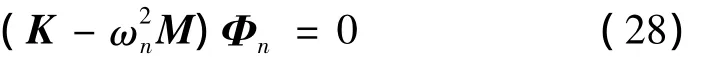
式中:K、D、M分别为裂纹管道的总刚度矩阵、阻尼矩阵和质量矩阵;ωn、Φn分别为固有圆频率和振型。

假设裂纹不引起结构质量矩阵的变化，则无裂纹管单元刚度矩阵和管单元一致质量矩阵分别表示为:

根据上述裂纹管有限元模型，可以计算任意裂纹位置、裂纹深度管类结构的固有频率和振型。

4 实例分析

应用建立的含非贯穿直裂纹管道的有限元模型，分析裂纹管结构的振动特性，实例模型如图3所示。管道长度 L为 1.0 m，内径 Di为 0.02 m，外径 De为0.04 m，密度ρ为7850 kg/m3，弹性模型 E 为206 GPa，泊松比 υ为0.27。

图3 裂纹管类结构示意图Fig.3 Sketch of the cracked pipe-like structure

为了直观描述变化规律定义无量纲参数，即固有频率变化率Fr，表达式如下:

图4和图5分别给出了悬臂约束、简支约束两种条件下含非贯穿直裂纹管道的前三阶固有频率随裂纹位置、深度的变化率Fr，图中x/L、a/t分别为裂纹相对位置和相对深度。

图4 裂纹管道的前3阶固有频率变化(悬臂约束)Fig.4 .Variations of the natural frequencies of the cracked pipe for the first three modes(cantilever constraint)

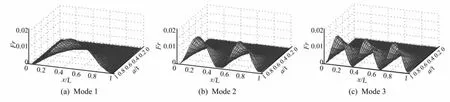
图5 裂纹管道的前3阶固有频率变化(简支约束)Fig.5 Variations of the natural frequencies of the cracked pipe for the first three modes(simple support constraint)

从图4和图5中可以看出:

(1)无论对于悬臂约束，还是简支约束，在裂纹位置相同条件下裂纹越深，其Fr值越大，固有频率降低越明显。

(2)在裂纹深度相同条件下，不同裂纹位置、不同边界约束条件以及不同阶次固有频率的Fr值也是不相同的。悬臂约束条件下，结构一阶固有频率呈现单调变化，裂纹距离固定端越近，裂纹越深Fr值越大，反之越小。简支约束条件下，Fr值分布关于x=0.5L对称。悬臂或简支约束条件下，结构二阶、三阶固有频率的Fr值并不随着裂纹位置的改变呈单调性变化，当裂纹越接近模态振型振幅为0的节点，结构固有频率变化越小;当裂纹越接近模态振型局部最大振幅的节点，结构固有频率变化越明显。

5 结论和展望

本文从断裂力学基本理论出发，推导了含非贯穿直裂纹管道在复杂联合荷载作用下的局部柔度系数，通过与Naniwadekar等人模型试验结果比较验证了本文局部柔度系数计算结果的合理性，为裂纹管的结构分析和裂纹识别提供了理论基础，克服了当前方法仅能针对特定的荷载模式或非空心截面的缺陷。

本文将管道视为梁－杆模型，避免了建立三维壳模型进行理论分析的难度，同时又有较高的精确度，可以满足工程需要。

根据建立的裂纹管有限元模型，研究了裂纹位置、裂纹深度与结构固有频率之间的关系。结果表明，当裂纹位于或接近模态振型振幅为0的节点时，裂纹对结构固有频率影响较小，而当裂纹位于或接近模态振型局部最大振幅的节点时，裂纹对结构固有频率影响显著。

本文研究了非贯穿直裂纹管局部柔度系数的求解方法以及固有振动特性，有关其它裂纹形式管的局部柔度系数求解方法和振动特性分析作者将另外讨论。

［1］Dimarogonas A D.Vibration of cracked structure:a state of the art review［J］.Engineering Fracture Mechanics，1996，55(5):831－857.

［2］胡家顺，冯 新，李 昕，等.裂纹梁振动分析和裂纹识别方法研究进展［J］.振动与冲击，2007，26(11):146－152.

［3］Irwin G R.Analysis of stresses and strains near the end of a crack traversing a plate［J］.Journal of Applied Mechanics.1957，24:361－364.

［4］Dimarogonas A D.Analytical methods in rotor dynamics［M］.Applied Science Publishers，Essex，1983.

［5］Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:A state of the art review［J］.Mechanical Systems and Signal Processing，2008，22(4):763－789.

［6］Papadopoulos C A.Some comments on the calculation of the local flexibility of cracked shafts［J］.Journal of Sound and Vibration 2004，278(4－5):1205－1211.

［7］Liu D，Gurgenci H，Veidt M.Crack detection in hollow section structures through the coupled response measurements［J］.2003，261(1)17 －29.

［8］Zheng D Y，Fan S.Vibration and stability of cracked hollowsectional beams［J］.Journal of Sound and Vibration，2003，267(4):933－954.

［9］Naniwadekar M R，Naik S S，Maiti S K.On predection of crack in different orientations in pipe using frequency based approach［J］.Mechanical Systems and Signal Processing，2008，22(3):693－708.

［10］Zheng D Y，Kessissoglou N J.Free vibration analysis of a cracked beam by finite element method［J］.Journal of Sound and Vibration，2004，273(3):457－475.

［11］Tada H，Paris P C，Irwin G R.The stress analysis of cracks handbook(ThirdEdition) ［M］.NewYork:ASME Press，2000.

［12］Gander W，Gautschi W.Adaptive Quadrature-Revisited［J］.BIT，2000，40:84－101.

［13］Nikolakopoulos P G，Katsareas D E，Papadopoulos C A.Crack identification in frame structures［J］.Computers and Structures，1997，64(1－4):389－406.