用于整星隔振效果评价的隔振器影响系数指标研究

涂奉臣，陈照波，刘旺中，方 勃

(1.哈尔滨工业大学 机电工程学院，哈尔滨 150001;2.哈尔滨工业大学 航天学院，哈尔滨 150001)

卫星发射的主动段一般只持续几分钟到十几分钟，但在这个过程中，卫星却处于十分恶劣的力学环境之中。概括来说，主动段内作用于卫星的动载荷包括正弦、随机及冲击等各种振动性质的激励，其频率从低频5 Hz到高频10 kHz［1］。这些来自于运载火箭的振动和冲击载荷将有可能导致卫星损坏或使其可靠性降低。为解决此问题，国内外航天界对整星隔振理论和技术进行了一系列研究［2－4］，取得了一定成果。通常，在整星隔振系统设计时，对隔振器的参数设计一般围绕隔振效果展开。因此，确定隔振效果评价指标是隔振效果评价体系的关键内容。完整的隔振效果评价体系应包含两方面内容:一是对整星隔振系统的隔振效果进行理论分析和预测;二是对实际整星隔振效果进行测定。目前常用的隔振效果评价指标有传递率、插入损失、振级落差和功率流等。通常以振动传递率作为隔振效果的理论预测依据，但是对于实际系统的隔振效果，通常采用插入损失或振级落差来评定。由于设计指标(传递率)未能与测量指标(插入损失或振级落差)一致，所以需采用更为合理的隔振效果评价指标。20世纪80年代，Goyder和 White［5］又提出了振动功率流概念，通过振动功率流指标来评价隔振效果。本文将在分析这几种评价指标及其应用局限性的基础上，提出一种改进的隔振器影响系数指标，用于对整星隔振效果进行理论分析预测和实测评价。

1 评价隔振效果的常用指标及其应用局限性

1.1 振动传递率

在理论研究和实际工程应用中，常采用隔振器底部到顶部的振动传递率作为隔振效果的评价指标，当传递率小于1时，认为隔振有效，并且传递率越小隔振效果越好。这种评价隔振效果的思想来源于单自由度的基础激振，并且是基于如下假设:被隔振体为刚体;隔振器的弹簧和阻尼器不计质量;基础为刚性［6］。但在整星隔振系统中，被隔振卫星为柔性，同时隔振器还具有分布质量，而且基础也不完全为刚性。如果此时仍采用隔振器底部到顶部的振动传递率来评价隔振效果，就有可能出现不准确甚至相反的结果。下面以实例说明此结论。

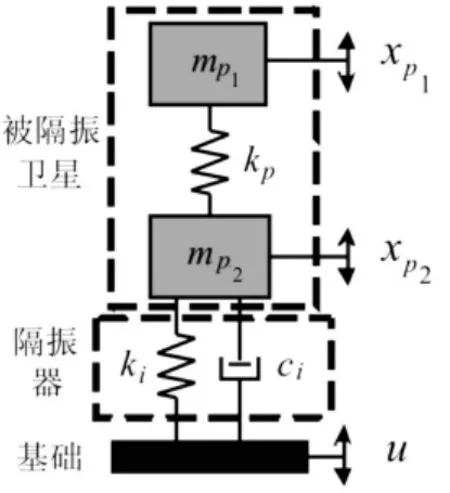
图1 两自由度卫星隔振系统Fig.1 Two-DOF isolation system

如图1所示，将被隔振卫星视为具有两个纵向自由度xp1和xp2，mp1和 mp2分别为两个自由度的集中质量，kp和ki分别为两自由度间的连接刚度和隔振器刚度，ci为隔振器的阻尼系数，则系统的动力学方程为:

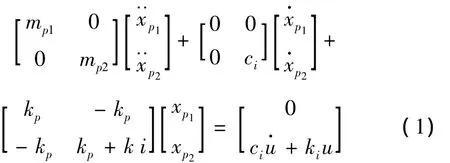
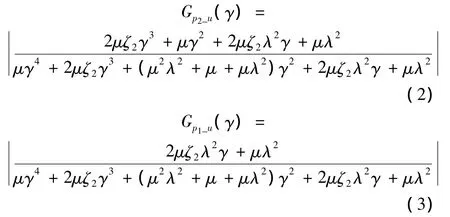
当取 μ =10，ζ2=0.1，λ =60 时，利用式(2)和式(3)计算得到卫星上两个自由度对基础激励的传递率曲线，如图2所示。当λ=60，即ω=ω1时，隔振器底部到顶部的传递率接近于零，而xp1对底部激励的传递率并不为零，这相当于上面的自由度充当了下面自由度的动力吸振 器。 所以，虽然隔振器底部到顶部的传递率较小，但隔振器底部到卫星上部的传递率未必就小。当卫星具有更多自由度时，隔振器顶部对底部的传递率会出现更多谷值，而对应谷值频率处，被隔振卫星上节点的传递率可能仍然很大。总之，当被隔振体为柔性体时，由于各点运动不再一致，只用隔振器底部到顶部的传递率来评价隔振效果是不充分的。

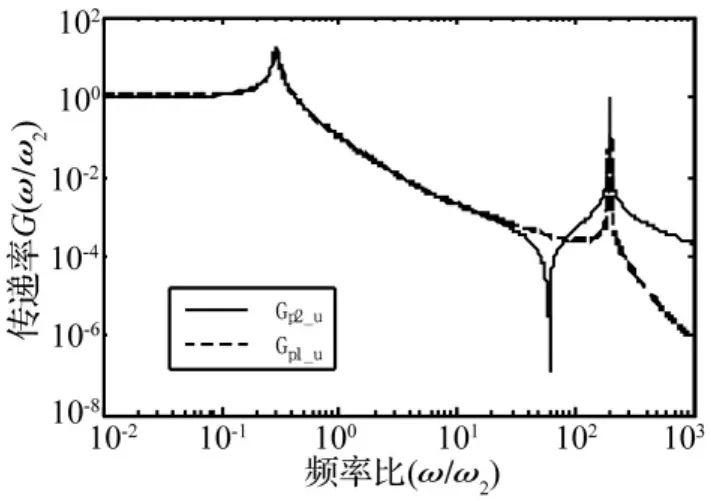
图2 两自由度卫星隔振系统的传递率Fig.2 Transmissibility of two-DOF isolation system

1.2 振级落差

隔振器振级落差定义为隔振器底部振动响应有效值与隔振器顶部振动响应有效值之比的常用对数的20倍。如果a1为隔振器底部的振动加速度响应，a2为隔振器顶部的振动加速度响应，卫星的加速度阻抗为ZS，隔振器的加速度阻抗为 ZI，运载火箭的加速度阻抗为ZR，则整星隔振器的加速度振级落差LD为:

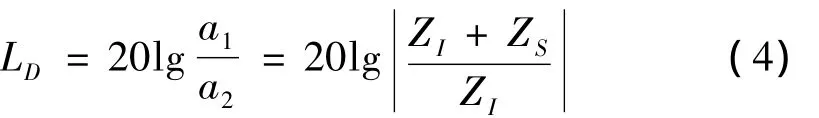
由式(4)可见，隔振器振级落差与运载火箭的加速度阻抗ZR无关，只取决于卫星和隔振器的阻抗特性。在隔振器一定的情况下，卫星阻抗特性的变化将对振级落差产生较大影响。由于卫星受到的振动载荷激励由多种频率成分组成，而隔振器中各个组成元件的阻抗特性也随着频率变化，因此在各个频率上的隔振效果不同。与振动传递率评价指标相似，采用隔振器振级落差来评价整星隔振效果也不充分。因为当隔振器底部激励频率与卫星本身的共振频率相同时，卫星充当了隔振器的动力吸振器，此时隔振器上端面振动微小，但卫星本身振动有可能很大。而从隔振器上下端面测量得到的隔振器振级落差指标却显示整星隔振效果良好。因此，隔振器振级落差这个评价指标并不能确切地反映真实的整星隔振效果，它只能作为一种粗略的评价指标。

1.3 功率流指标用于隔振效果评价

振动功率流分析理论是基于振动的传递是一种能量传递的观点。振动功率流既包含力和速度的幅值大小，也考虑它们之间的相位关系，可在结构上某点通过测试获得。对振动系统采用功率流分析，易于理解振动传输机理，可将振源功率、系统损耗功率和结构储能变化率联系起来进行研究。对于隔振系统的性能，可采用功率流理论进行预测和评价，即通过分析输入到结构的功率流、振动传输路径的功率流来预测及评价隔振效果［7］。

由于功率流是一个绝对量，其本身不反映隔振效果，因此需用相对指标来衡量隔振效果。常用的指标是功率流传递率和传递功率流落差。功率流传递率通常作为设计预测指标，而实测功率流落差作为功率流传递率设计指标的辅助指标，来对系统的隔振效果进行综合评价。由功率流传递率设计指标与传递功率流落差实测指标构成的隔振效果评估体系，比传统的振动传递率与振级落差的组合更合理。

但由于整星隔振系统中的功率流测量较为困难，工程上应用不方便，限制了其应用，所以下面提出一种采用改进的隔振器影响系数方法来预测和评价整星隔振效果。

2 改进的隔振器影响系数指标

2.1 改进的隔振器影响系数定义

针对隔振器底部到顶部的传递率、振级落差和功率流等作为整星隔振效果评价指标的应用局限性，刘丽坤等人曾经引入隔振器影响系数指标来评价隔振性能，其定义为:

式中，Ri为卫星和火箭之间不采用隔振器连接时卫星上第i个观测点的响应;RIi为卫星和火箭之间采用隔振器连接时卫星上第i个观测点的响应。当Ei＞1时隔振有效，且Ei的值越大，隔振效果越好［8］。

这个指标采用卫星上一系列关键点的隔振器影响系数来评价隔振性能，需得到较多的隔振器影响系数曲线。对于纵向振动，卫星上不同观测点的隔振器影响系数曲线基本重合，这是因为卫星、隔振器和运载火箭的结构基本上关于轴线对称，隔振器的纵向方程与其它方向不耦合，所以对于纵向振动，整星隔振系统相当于火箭与卫星通过一个隔振器相连的情况，此时隔振器影响系数与观测点的选取基本无关;但对于横向振动，不同观测点的隔振器影响系数差别较大。为了达到纵向和横向的隔振器影响系数统一，同时希望通过较少的曲线就能直观地评价隔振效果，这里在原有隔振器影响系数基础上，提出一种改进的隔振器影响系数指标，其定义为:

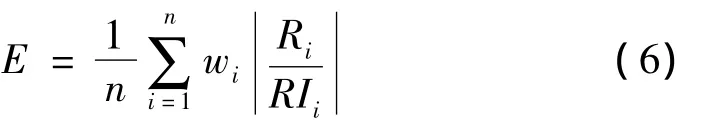
式中wi为第i个观测点在E中所占重要程度的权函数，对于卫星顶部等振动相对较大的部位，wi的取值较大。E这个指标综合反映了采用隔振器后卫星上各观测点的振动响应相对于隔振前的情况。

由于采用质量、刚度和阻尼等矩阵形式来表示火箭或卫星的动力学特性很繁杂，下面采用位移导纳来表达改进的隔振器影响系数。

为便于分析，将整星隔振器等效成多个并联的单向隔振器。图3为柔性卫星与运载火箭通过N个隔振器连接构成的整星隔振系统示意图。运载火箭在T点受激励力FT作用，FS=［FS1，…，FSN］T表示火箭对隔振器的作用力向量，FR=［FR1，…，FRN］T表示隔振器对卫星的作用力向量，ws表示运载火箭上与隔振器相连的N个点的位移，它等于隔振器上对应连接点的位移wA。则位移wS可表示为:

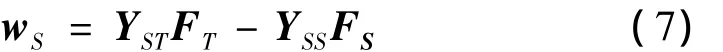
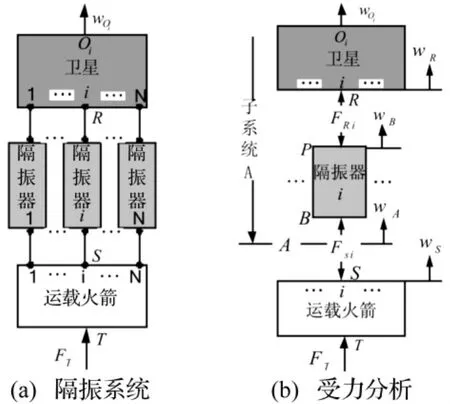
图3 整星隔振系统示意图Fig.3 Diagram of WSVI system

式中，YST为火箭激振点T到与隔振器连接点S的传递导纳矩阵，YSS为火箭和隔振器连接点的直接位移导纳和各点间的传递位移导纳构成的位移导纳矩阵。

位移wA可表示为:

YAA为隔振器与火箭连接点的直接位移导纳和各点间的传递位移导纳构成的位移导纳矩阵。由于wS=wA，利用式(7)和式(8)可得:

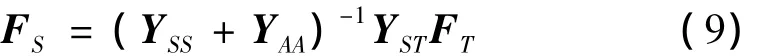
YAA和FR的表达式为:

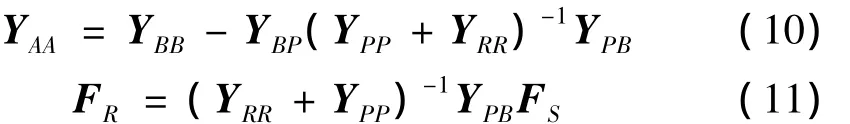
其中，YRR为卫星与隔振器连接点的直接位移导纳和各点间的传递位移导纳构成的位移导纳矩阵，YPP为隔振器上P点的直接位移导纳矩阵，YPP和YPB是隔振器的传递位移导纳矩阵，YPP、YBP和YPB均为对角矩阵。

卫星上的观测点Oi的位移为:

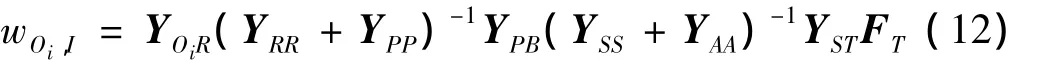
其中YOiR为从R点到观测点Oi的传递位移导纳矩阵。

当卫星与运载火箭直接相连时，卫星上观测点Oi的位移为:

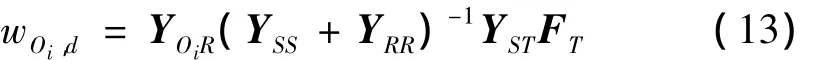
由式(12)、式(13)和改进隔振器影响系数的定义式(6)，得到当在卫星上取n个观测点时，采用位移导纳表达的改进隔振器影响系数为:

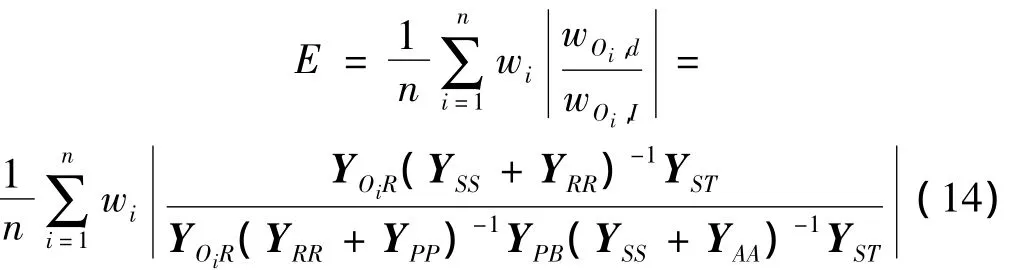
由式(14)可见，改进的隔振器影响系数只与卫星、隔振平台和运载火箭相应位移导纳及卫星上观测点的选择有关。由于相应位移导纳是卫星、隔振平台和运载火箭固有的，所以当卫星观测点一定时，指标E是确定的。只要知道了式(14)中的各个位移导纳，就可计算出整星隔振系统的改进隔振器影响系数。由于位移导纳、速度导纳和加速度导纳之间是等效的，所以也可以采用速度导纳或加速度导纳的形式来表达E。下面就以自行设计的新型整星隔振平台为例，论述确定各个位移导纳的方法。

2.2 确定位移导纳

本文算例中采用自行研制的曲杆固接式新型整星隔振平台，其结构如图4所示。上下平台为圆环形结构，上下平台之间由6根轻质、高强度的碳纤维增强铝复合材料制成的弹性支承杆连接。为降低隔振平台轴向刚度，每根支承杆中部弯制成圆弧形。在降低轴向刚度的同时，隔振平台的横向倾覆刚度也会相应有较大程度降低，这对于卫星隔振系统的横向稳定性不利。所以在平台中加入了防止横向摇晃的套筒式防摇结构，该结构提高了平台的横向和倾覆刚度，却不会使轴向和周向转动刚度提高。为兼顾高频隔振和抑制低频共振响应，在弹性支承杆的弯曲处加入可调节阻尼力的磁流变阻尼器，通过调节磁流变阻尼器的输入电流来改变隔振平台的耗能能力。

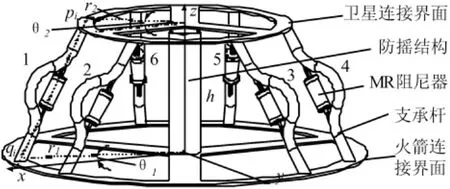
图4 采用磁流变阻尼器的整星隔振平台结构Fig.4 WSVIP with MR dampers

为得到式(14)中的各个位移导纳，需分别建立卫星、曲杆固接式隔振平台和运载火箭的动力学模型，然后将3个模型综合成整星隔振系统的总体模型。首先建立基础激励下的新型隔振平台的动力学方程，由于隔振平台与卫星连接面及运载火箭连接界面的刚度较大，可近似表示成一个节点，这样的简化在低频段是满足工程设计要求的。此外卫星和运载火箭的有限元模型维数很高，通常需要降阶处理，只保留低频段模态。

建立新型隔振平台动力学方程的过程较繁琐，且不是本文研究的重点内容，这里直接写出隔振平台动力学方程经过拉普拉斯变换后的简洁形式，如下式:

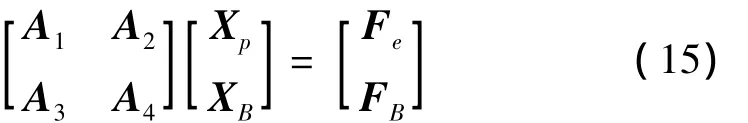
其中，Xp为隔振平台上平台的自由度，XB为下平台的自由度。Fe为卫星底部对隔振平台上表面的作用力，FB为隔振平台底部受到的作用力。子矩阵A1，A2，A3和A4均由质量、阻尼和刚度矩阵组合而成。

柔性卫星采用有限元方法建模，离散化的动力学模型首先进行坐标变换后得到模态坐标下的卫星动力学方程，再经过拉普拉斯变换后得到如下简洁表达式:

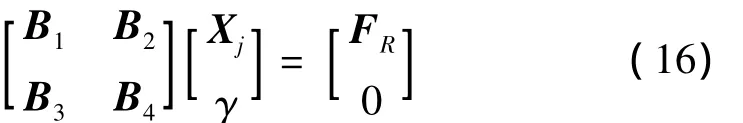
式中，Xj为卫星底部边界点的自由度，与隔振平台上表面固接;γ为卫星的模态坐标;FR为隔振平台对卫星底部的作用力;子矩阵B1，B2，B3和B4均由质量、阻尼和刚度矩阵组合而成。

运载火箭也采用有限元方法建模［9］，离散化的动力学模型缩聚后可写成:

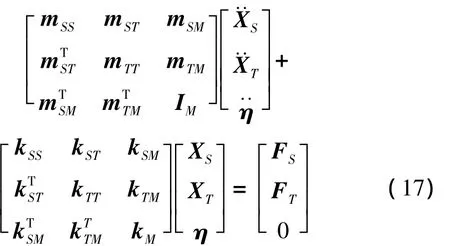
如果考虑运载火箭中的阻尼作用，可采用比例阻尼或结构阻尼。对上式进行拉普拉斯变化后得到简洁表达式如下:

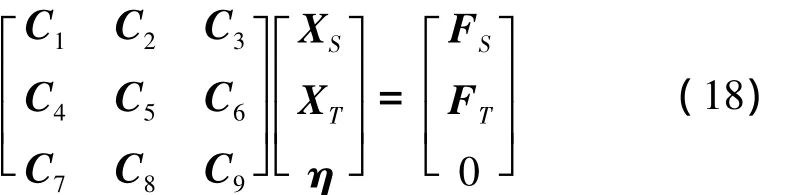
以上两式中，XS为运载火箭与隔振平台底部连接面的自由度;XT为火箭底部自由度;η为火箭箭体的模态坐标;FS为隔振平台底部对火箭的作用力;FT为火箭底部受到的发动机激振力;子矩阵C1，C2，…，C9均由质量、阻尼和刚度矩阵组合而成。

根据式(15)、式(16)和位移导纳定义，可得位移导纳:

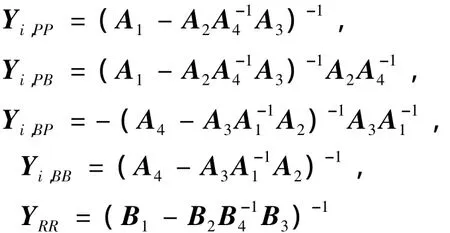
卫星上的观测点Oi到与隔振器的连结点R的传递导纳为YOiR，可表示为:

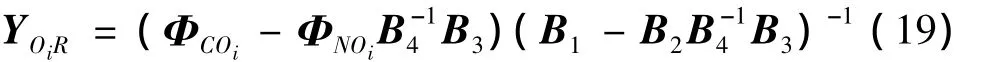
其中ΦNOi和ΦCOi分别为卫星的正则主模态矩阵ΦN和约束模态矩阵ΦC中节点Oi对应的行。

利用式(18)，可得位移导纳:

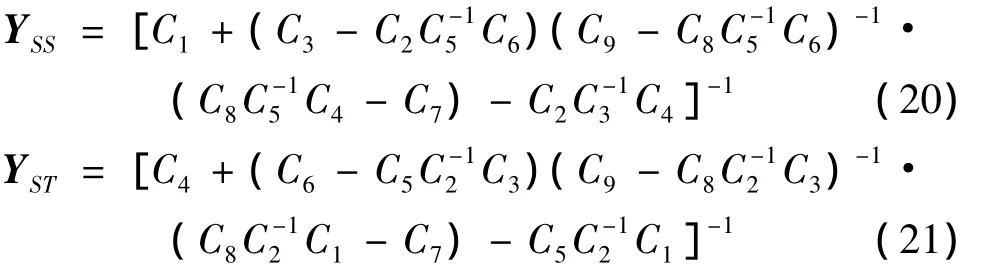
将以上通过理论计算得到的位移导纳代入到式(14)中即可计算得到改进的隔振器影响系数E。

3 整星隔振效果预测实例

当采用改进隔振器影响系数E来预测新型整星隔振系统的性能时，首先建立新型整星隔振系统的有限元模型，如图5所示，其中图5(a)为卫星－新型隔振平台的有限元模型，图5(b)为运载火箭的有限元模型。然后选取卫星上6个观测点，通过有限元方法计算得到卫星、隔振平台和运载火箭上所需的直接导纳和传递导纳，代入到式(14)中计算得出改进的隔振器影响系数E，其中卫星上6个观测点的权系数wi从上至下取为:1，1，1，0.8，0.5，0.5。图 6 为新型整星隔振系统的改进隔振器影响系数E曲线，可见，在纵向和横向上除了在部分低频区域内E的值小于1外，其余频段内E的值均大于1。即通过分析改进隔振器影响系数E的曲线图，可以预测出以下结果:采用曲杆固接式新型隔振器平台时，在绝大部分频域范围内可取得良好的被动隔振效果。

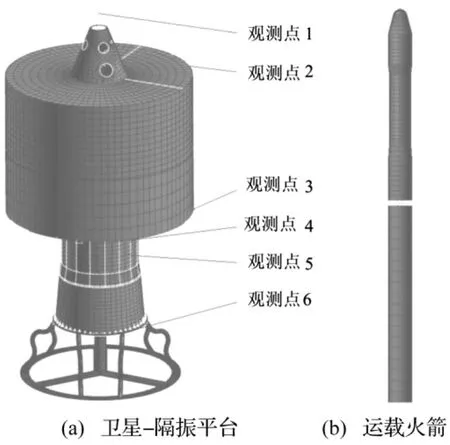
图5 整星隔振系统的有限元模型Fig.5 FE models of WSVI system

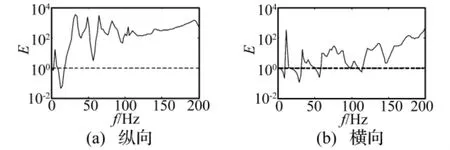
图6 改进的隔振器影响系数曲线Fig.6 Weighted influence coefficients of the isolator

在低频的部分区域内E的值小于1，说明在此频段内，采用曲杆固接式新型隔振平台后卫星上观测点的运动响应大于隔振前。这种情况下，可增大隔振平台中磁流变阻尼器的阻尼系数，进而降低卫星的振动响应。而在其它频段内，磁流变阻尼器维持小电流输入或不工作，整星隔振系统即能够取得良好的隔振效果。即新型隔振平台能够实现整星的主被动一体化隔振控制。

由式(14)可知，指标E用位移导纳表达和用观测点的振动响应来表达是等价的，这样就可以通过测量采用隔振平台前后观测点的响应来得到实际的指标E，而不需要测量难以准确测量的位移导纳。通常，测量卫星上关键点的运动响应是比较方便的。在实测隔振性能时，在6个对应的观测点上布置运动传感器，测得采用新型隔振平台前后观测点的运动响应，并利用改进的隔振器影响系数定义式(6)计算出改进的隔振器影响系数，并将其与仿真预测阶段得到的E比较，实现预测指标和测量指标的统一。

4 结论

在对柔性卫星隔振系统进行隔振效果评价时，采用隔振器底端到顶端的传递率和隔振器振级落差来评价隔振性能是不充分的，而功率流指标也在实际工程应用中存在测量困难的局限性。

改进隔振器影响系数指标形式简单，表达直观，可采用机械导纳来表达，只要通过仿真计算得到卫星、隔振平台和运载火箭的相应机械导纳，就可以很方便地计算改进的隔振器影响系数，从而对整星隔振效果进行预测。对于自行设计的新型整星隔振平台，采用改进隔振器影响系数指标进行隔振效果预测，得到了良好的隔振性能。改进隔振器影响系数与卫星上观测点的选取及整个系统部件的动力学特性有关。通过测量隔振前后卫星上观测点的运动响应可得到实测的隔振器影响系数指标，可将其与预测结果进行比较，实现预测指标和实测指标的统一。

［1］赵会光，马兴瑞，冯纪生.整星隔振技术若干问题的探讨［J］.航天器工程，2001，10(3):30 －37.

［2］Wilke P S，Johnson C D，Fosness E R.Whole-spacecraft passive launch isolation［J］.Journal of Spacecraft and Rockets，1998，35(5):690 －694.

［3］Maly J R，Fowler E C，Biskner A C，et al.Structural models and dynamic measurements ofsatellite launch adapter structures［A］.50thAIAA/ASME/ASME/ASCE/AHS/ASC Structures，Structural dynamics，and materials conference，4－7 May 2009，palm springs，california:1 －12.

［4］Liu L K，Liang L，Zheng G T，et al.Dynamic design of octostrut platform for launch stage whole-spacecraft vibration isolation［J］.Journal of Spacecraft and Rockets，2005，42(4):654－662.

［5］Goyder H G，White R G.Vibrational power flow from machines into built-up structure，PartⅠ:Introduction and approximate analyses of beam and plate-like foundations［J］.Journal of Sound and Vibration，1980，68(1):59－75.

［6］Sciulli D，Inman D J.Isolation design for a flexible system［J］.Journal of Sound and Vibration，1998，216(2):251－267.

［7］孔 杰，张蔚波，牛军川.功率流理论在柔性振动控制技术中的应用与发展［J］.机械工程学报，2003，39(9):23－28.

［8］刘丽坤.八作动器隔振平台及整星隔振研究［D］.哈尔滨:哈尔滨工业大学，2005.

［9］Liu L K，Zheng G T.Parameter analysis of PAF for wholespacecraft［J］.Aerospace Science and Technology，2007，11:464－472.