带递归的模糊感知器有限收敛性
刘 燕, 杨 洁, 李 龙
(1.大连理工大学 数学科学学院,辽宁 大连 116024;2.大连工业大学 信息科学与工程学院,辽宁 大连 116034;3.衡阳师范学院 数学与计算科学系,湖南 衡阳 421008)
0 引 言
模糊逻辑和神经网络在信息处理系统中各有其优缺点,最近,许多学者的工作都致力于将模糊系统与神经网络结合在一起,其中对模糊神经网络有很多的关注.文献[1、2]提出了模糊感知器的一些学习算法;文献[3]对0阶Takagi-Sugeno推理系统的学习算法进行了收敛性证明;文献[4、5]对多层模糊感知器进行了研究.
具有递归环节的动态模糊神经网络可以解决静态网络无法处理的暂态问题.FRNN(模糊递归神经网络)通过在网络输入层中加入递归连接,使网络具有动态映射能力,从而对动态系统有更好的响应.
如果训练样本线性可分,传统的感知器算法能在有限步确定一个线性决策边界,从而分离这两类训练样本[6、7].对于模糊感知器,文献[8]提出了一种新的训练算法,并证明当样本可分时,该算法有限收敛.那么,在模糊感知器中加入递归单元是否还能得到算法的收敛性?本文将对这个问题进行讨论,给出若训练样本模糊可分,在一定条件下,带递归的模糊感知器算法有限收敛的结论及证明.证明过程的难点和关键在于确认递归项权值在学习过程中的单调递减性.
1 带递归的模糊感知器的结构及梯度学习算法
1.1 带递归的模糊感知器的结构
本文研究的是具有n个外部模糊输入单元、一个输出单元和一个递归神经元的感知器.其结构如图1所示,网络的模糊训练样本对为{ξ(s),其 中是n维模糊输入向量,O(s)是其理想输出.

图1 具有n-1-1结构的递归模糊感知器的结构Fig.1 The structure of recurrent fuzzy perceptron with n-1-1structure
将这些样本随机排列组成一个无穷序列{ξk,其中每个样本对{ξ(s),O(s)}出现无穷多次∈[0,1]n,为网络在第k时刻的外部输入向量,网络第k时刻递归层的输入
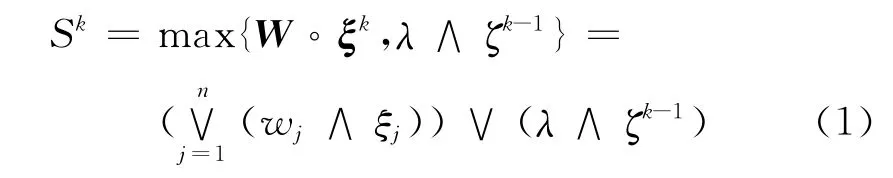
其中ζ0=0,递归层的输出为
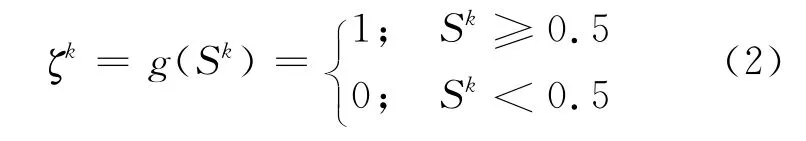
其中 ∨ 是取大运算;∧ 是取小运算;代表max-min(∨ -∧)合成算子;权重向量W =(w1w2… wn)T∈ [0,1]n,其中 wj(j=1,2,…,n)代表连接第j个外部输入神经元和输出神经元的权值;连接递归神经元和输出神经元的权值为λ,λ∈ [0,1].
网络的训练目标是对给定的激活函数g(x):R→{0,1},确定权值(W,λ)∈ [0,1]n×[0,1],使得训练样本能够被正确地分类,即ζ(ξ(s))-O(ξ(s))=0.
为证明方便,记理想输出为O(s)=0的样本为Xm,m=1,2,…,M,1≤M<S;另一些对应理想输出O(s)=1的样本,记为Yp,p=1,2,…,P,1≤P<S,M+P=S.定义两个集合:ΦM={1,2,…,M},ΦP= {1,2,…,P}.
假设训练样本可分,即存在一个模糊向量A=(a1a2… an)T∈ [0,1]n使得

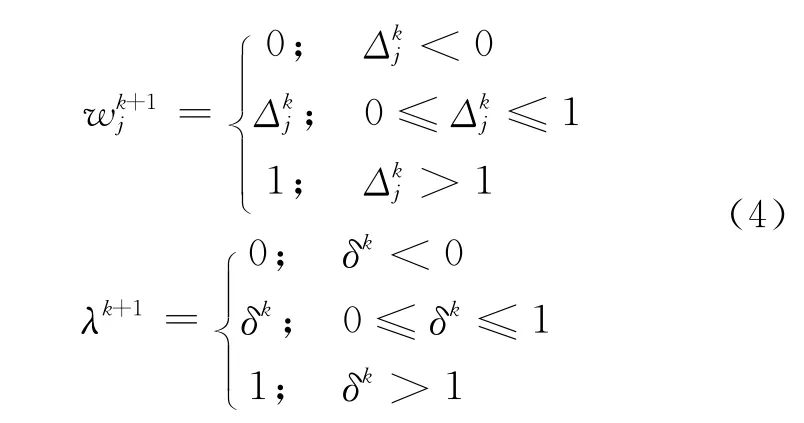
1.2 样本集性质
首先对训练样本做一个假设[8].
假设Ⅰ 对任意一个m∈ΦM,至少存在一个m0,使得
下面给出模糊训练样本对的3条重要性质[8].
性质1 对式(3)中模糊向量A,存在下标j1与j2,使得aj1≥0.5与aj2<0.5分别成立.
基于性质1,不失一般性,假设存在正整数q,1≤q<n,使得a1,…,aq≥0.5,aq+1,…,an<0.5.
性质3 对每一个Yp,p=1,2,…,P,至少存在一个rp≤q,使得
接下来给出训练样本的另一个假设[8].
假设Ⅱ 对任意一个j,R<j≤n,至少存在一个mj,使得对每个1≤j≤q,至少存在一个pj,使得
2 有限收敛定理
在这一部分,分别给出迭代算法式(4)在n=2和n>2两种情况下的收敛结果.
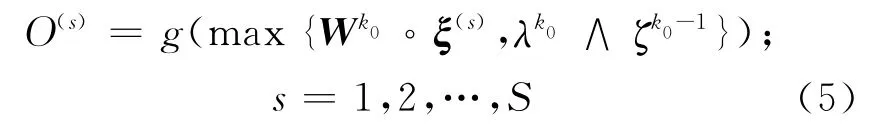
定理1 当n=2时,若假设Ⅰ和Ⅱ成立,则算法式(4)有限收敛.
首先证明wk1<0.5的情况下,权值的迭代不会停止.事实上,若wk1<0.5且wk2≥0.5,那么对所有λk和ζk-1,都有
图书馆是全面系统地收藏着人类发展过程中所创造和积累的文献信息资源集散地,又是人类文明、科技进步等的守护者与传承者。文献信息资源的传播不受地域与时空限制,首先图书馆能够把历代学者所创造和积累的各种文献信息载体保存下来,并传递给需要它的每位读者,其次图书馆之间又能以开展的资源共享和馆际互借等方式把不同地域的学者所创造的文化精神作品及时传递给需要它的需求者。图书馆以服务型社会理论为指导,坚持”以人为本,读者至上”人性化服务的原则,能够在读者的不同年龄阶段,不同时间,满足读者不同层次的需求,读者可以利用图书馆文献资源各取所需,充分发挥自己的阅读能力,开展自由自在的阅读与研究活动,提高自身的综合素养。

则
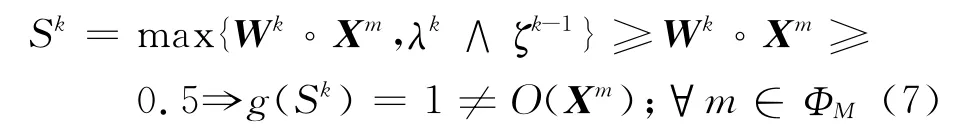
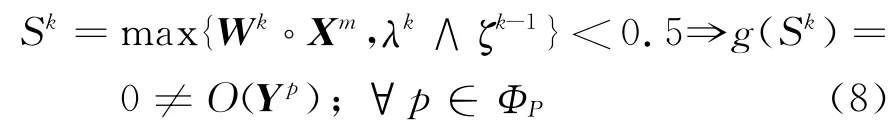
若λk≥0.5,有
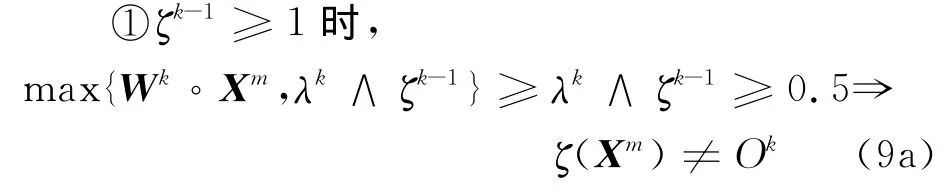
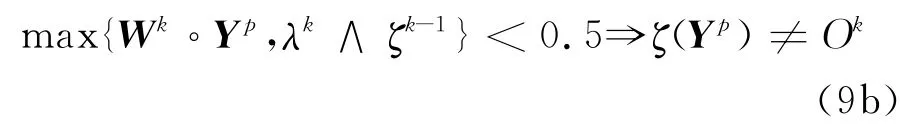

从而g(Sk)=1=O(Yp),p∈ΦP.由的单调不减性知,当k≥K1时,对{(Wk,λk)}真正起更新作用的只有因此,在无穷序列中除去
现在令k≥K1,若且λk<0.5,则对ζk-1,(Wk,λk)满足式(5),已是所求的解.否则,若对λk和ζk-1,有
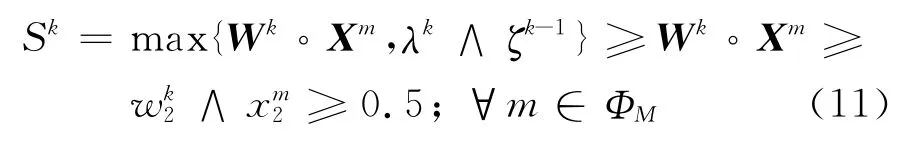
故ζ(SK)=1≠O(Xm).因此{(Wk,λk)}的迭代不会停止.
接下来,考虑n>2的情况.为了保证收敛性,需要一些比较强的条件.
定理2 若假设Ⅰ和Ⅱ满足,那么在以下条件成立时,算法式(4)有限收敛:
(a)存在一个r0,1≤r0≤q,使得p∈ΦP成立;
证明 由定理2条件(a)和性质2,有η(Ok-,从而注意到当ξk没被正确分类时,不等式严格成立.那么若达到0.5之前,(Wk,λk)满足式(5),则算法式(4)有限收敛;否则,若,注意到其他权值的更新不影响的单调不减性,故在真正迭代有限步之后,会有即存在正整数K5,使得当k≥K5,有且WkYp≥

现令k≥K5,若wkj<0.5,j=R+1,…,n,且λk<0.5,则
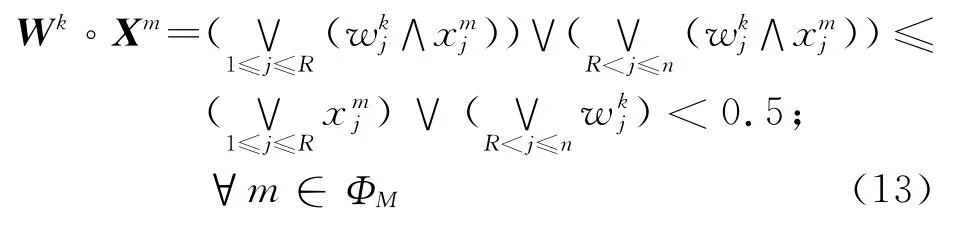
从而对ξk-1,都有Sk=max{WkXm,λk∧ζk-1}<0.5,那么式(5)成立,即(Wk,λk)已经是所求的解.
若λk≥0.5,当ζk-1=0时,仍有Sk<0.5,从而式(5)成立;若ζk-1=1,则
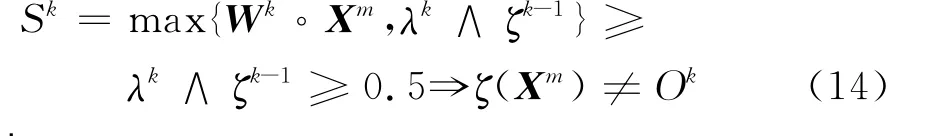
则

从而存在正整数K6,使得当k≥K6时,λk<0.5.
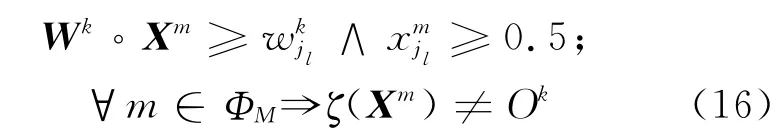
说明(Wk,λk)不能将正确地分类,即使只有一个与ζk-1=1)成立,式(5)就不成立,且有

由定理2条件 (b),可 得η(Ok-ζk)(ξjm-0.5)≤0,R<j≤n,故.结合假设Ⅱ,有成立,那么对每一个l=
1,2,…,L,存在.因此,存在Kjl∈N,s.t.当成立.令则当1,…,n,此时式(5)成立,故算法式(4)有限收敛.证毕.
3 结 论
本文考虑的是带递归的模糊感知器的有限收敛问题,其内部运算基于max-min模糊逻辑运算,并且网络结构类似于内部运算基于加法-乘法的传统感知器.如果训练样本线性可分,传统的感知器算法能通过有限步的权值学习来分离属于不同类别的训练样本.本文拓广了文献[8]的结论,对递归模糊感知器学习算法的有限收敛性进行了探讨.
1] LI L,YANG J,LIU Y,etal.Finite convergence of fuzzy delta rule for a fuzzy perceptron[J].Neural Network World,2008,18(6):459-467
[2] CHEN J L,CHANG J Y.Fuzzy perceptron learning and its application to classifiers with numerical data and linguistic knowledge[J].IEEE Transactions on Fuzzy Systems,2000,8(6):730-745
[3] WU W,LI L,YANG J,etal.A modified gradientbased neuro-fuzzy learning algorithm and its convergence [J]. Information Sciences, 2010,180(9):1630-1642
[4] MITRA S,PAL S K.Fuzzy multi-layer perceptron,inferencing and rule generation [J]. IEEE Transactions on Neural Networks,1995,6(1):51-63
[5] PAL S K,MITRA S.Multi-layer perceptron,fuzzy sets,and classification [J].IEEE Transactions on Neural Networks,1992,3(5):683-697
[6] WU W,SHAO Z Q.Convergence of online gradient methods for continuous perceptrons with linearly separable training patterns[J].Applied Mathematics Letters,2003,16(7):999-1002
[7] SHAO Z Q,WU W,YANG J.Finite convergence of on-line BP neural networks with linearly separable training patterns [J].Journal of Mathematical Research and Exposition,2006,26(3):451-456
[8] YANG J,WU W,SHAO Z Q.A new training algorithm for a fuzzy perceptron and its convergence[C]//ISNN2005,Lecture Notes in Computer Science.Berlin:Springer,2005:609-614

