逆系统轨迹控制二级倒立摆自动摆起
张 永 立, 程 会 锋, 李 洪 兴
(大连理工大学 电子信息与电气工程学部,辽宁 大连 116024)
0 引 言
倒立摆系统具有强非线性和不确定性,并且对外部干扰极其敏感,是广泛用于教学和理论研究的典型平衡控制范例和欠驱动控制系统.另外,倒立摆的研究对工业过程中的控制问题具有一定的指导意义和应用价值.目前,关于倒立摆的研究主要分为两个方面:一是倒立摆系统的稳定控制[1~4],二是倒立摆系统的自动摆起控制[5~14].对二级倒立摆控制系统的研究成果很多,李祖枢等采用仿人智能控制方法,实现了二级倒立摆系统的自动摆起控制[9、11].逆系统方法[10、15~18]是直观实用的非线性控制方法,文献[10、15、16]对逆系统轨迹控制方法的应用进行了研究,并结合基于LQR的增益调度反馈控制实现了二级倒立摆的自动摆起.
与文献[10]不同,本文采用逆系统前馈控制与H∞增益调度反馈控制相结合来实现二级倒立摆的自动摆起,并设计变增益H∞反馈控制器在稳摆控制阶段进行稳定控制.
1 模型建立
二级倒立摆主要由小车、摆杆1、摆杆2组成,它们之间自由链接,如图1所示.a为小车的加速度,x为小车的位移,θi(i=1,2)为摆杆i与摆杆竖直方向的夹角,Oi、Gi为摆杆i的链接点与质心的位置.二级倒立摆系统的具体物理参数见表1.
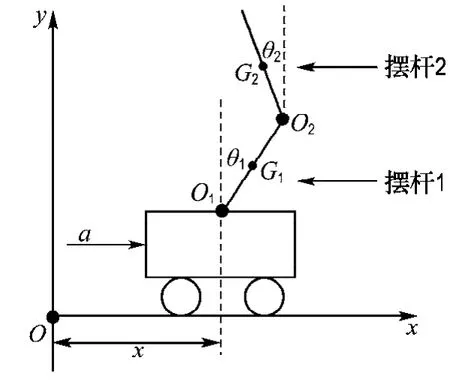
图1 二级倒立摆系统简化结构Fig.1 The simplified structure of the double inverted pendulum

表1 二级倒立摆物理参数Tab.1 Physical parameters of the double inverted pendulum
采用分析力学中的Lagrangian方程建模,得到如下二级倒立摆模型.

于是,方程组(1)可以写成

其中θ= (θ1θ2)T,向量函数α= (α1α2)T.取状态向量根据式(2)、(3)容易得到n=6维的二级倒立摆的状态方程
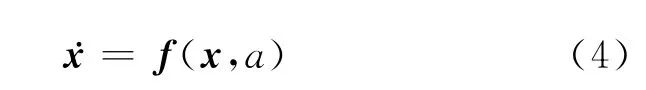
其中向量函数f=(f1f2…f6)T.
2 控制器的设计
二级倒立摆自动摆起控制有两个控制阶段.首先,将两摆杆从悬垂位置摆起到竖直倒立位置;其次,将两杆稳定在倒立平衡位置.本文采用基于逆系统的前馈控制和H∞增益调度反馈控制相结合的两自由度 (2DOF)控制策略进行摆起控制;在两摆杆摆起到倒立位置后,问题转化为平衡控制问题,采用变增益H∞反馈控制来实现对倒立摆的稳定控制.如图2所示,图中x、x*分别为小车位移的实际轨迹和参考轨迹,θ、θ*分别为摆杆摆角的实际轨迹和参考轨迹.
2.1 逆系统前馈控制
逆系统方法作为反馈线性化方法的一种,是比较直观且实用的非线性控制方法,广泛应用于工业机器人控制、过程控制及航天飞行器等领域.所谓系统Σ的逆系统Π,就是指以系统Σ预期的输出y*(t)作为系统Π的输入来产生系统Σ的控制a*(t),以驱动原系统Σ,从而使得其输出y(t)与所希望的输出y*(t)一致,即y(t)=y*(t).
针对二级倒立摆的数学模型,将方程(2)作为系统的输入输出动态,其中,a为系统的输入量,x为系统的输出量.很明显=a,那么可得系统的相对度r=2.方程组(3)是系统的内部动态.因此,如果给定某摆起轨迹x*,使得该控制系统严格沿着轨迹x*运动,那么,根据逆系统轨迹控制原理,前馈控制可取


图2 二级倒立摆的自动摆起和稳定控制框图Fig.2 The block diagram of swing-up and stabilizing of the double inverted pendulum
这时总有x=x*成立.如何获得合理的参考轨迹x*是以下要讨论的问题.
2.1.1 两点边值问题 二级倒立摆系统在有限时间t∈[0,T]内,从静止悬垂状态自动摆起到竖直倒立位置的过程满足如下边值条件:

其中式(6)为初值条件,式(7)为终值条件.另外,根据硬件的性能,并考虑到二级倒立摆控制系统的强不稳定性,在摆起过程中小车的运动轨迹须满足

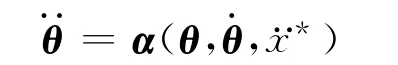
令

则得


很显然方程(9)和条件(10)是一个超定非线性两点边值问题.求解超定两点边值问题时需要n-r=4个附加参数才能求解.一般地,设参考轨迹函数为
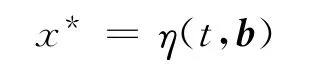
其中b=(b1b2b3b4),为附加自由参数.
2.1.2 参考轨迹 参考轨迹x*=η(t,b)的设计方法很多,一般情况下要求输入a*(t)连续,因此η(t,b)必须满足r(r=2)次可微.常用的轨迹方程有多项式函数和余弦级数.
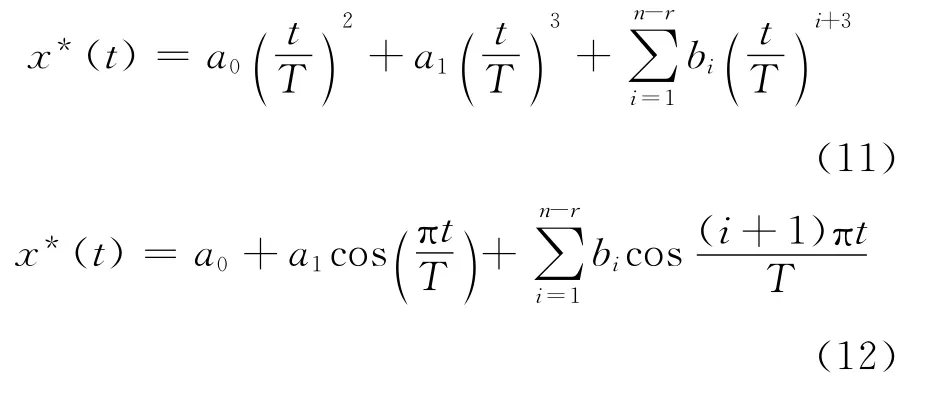
其中式(11)为多项式函数,式(12)为余弦级数.考虑到在数值计算上余弦级数的稳定性比较好,因此这里选用余弦级数来设计参考轨迹函数x*=η(t,b).此外,由条件(10)可得
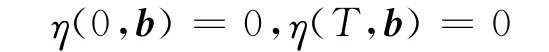
于是有
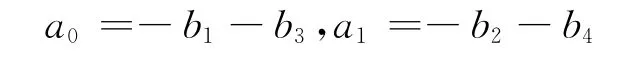
将式(12)代入式(9),利用函数bvp4c解得随时间t变化的参考轨迹θ*(t)和自由参数b=(b1b2b3b4).再由式(12)得到x*,进而求出于是根据方程(5)就可以很容易得到前馈控制a*.
分别选取T为1.9、2.2、2.5s时,得到的参考轨迹如图3所示;表2为对应于摆起时间T的自由参数b= (b1b2b3b4).
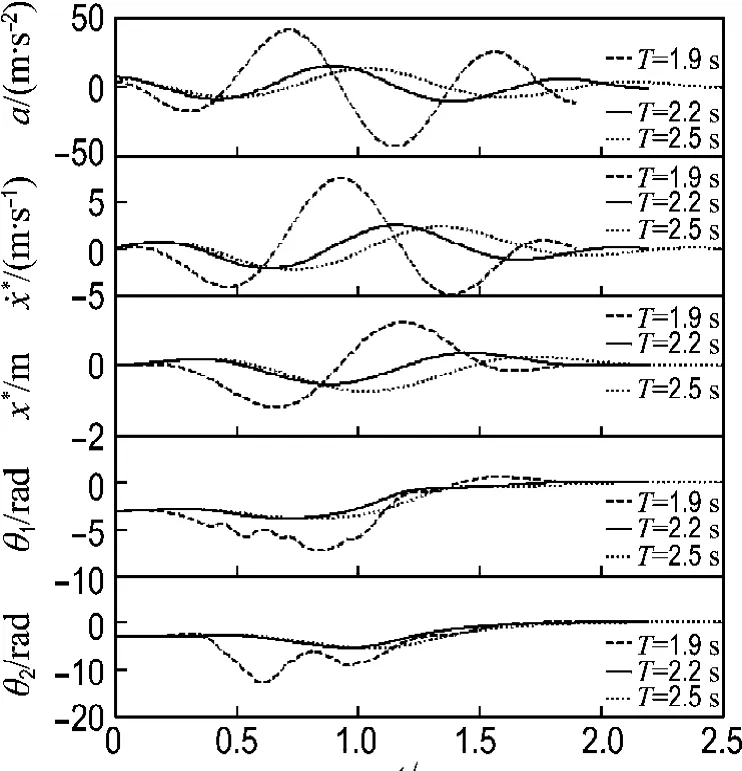
图3 x*为余弦级数时二级倒立摆自动摆起参考轨迹Fig.3 Reference trajectories for the swing-up of the double inverted pendulum when x*is a cosine series

表2 对应于不同T的自由参数bTab.2 Free parameter bcorresponding to T
由图3可以看出,T是一个重要的参数,它的选择受条件(8)和方程(9)的限制.T的取值对x*有很大影响.由于受机电系统响应速度的限制,T取值不能太小,否则将导致失控;此外,目前只能通过数值方法得到常微分方程两点边值的数值解,受此限制,T也不能取值过小,否则将会导致两点边值问题无解,或者得到一个不合实际的解,同样使系统不能得到有效控制.在数值求解过程中,如果增大T的取值,在实际控制中将使得摆杆摆起的时间延长.由于各摆杆之间为无约束自由链接,如果摆起时间太长,则会引起摆杆摆起的空中姿态失调,从而导致控制失败.因此,T的取值不能太大.由图3可知,当T=1.9s时参考轨迹的振幅明显超出了约束条件(8)的要求;当T=2.5s时,小车的移动范围明显增大.因此,根据以上分析选择T=2.2s.
需要注意的是,在使用bvp4c函数求解常微分方程的两点边值问题时,网格点tk∈[0,T]的数量要设置合理,并且要采用合理的方法估计网格点上的初值θt=tk,本文网格点数量选取为5,并采用两点三次埃尔米特插值方法进行初值估计.
2.2 H∞增益调度反馈控制
在摆起时间t∈[0,T]内,将二级倒立摆系统(4)沿着参考轨迹,通过泰勒展开方法进行线性化得其状态空间方程:

考虑到实际系统中具有许多不确定因素,例如系统参数的测量误差、小车轨道上的干摩擦、电气系统的输出误差等.这里假设小车轨道上的干摩擦为外界不确定干扰w,可以将方程(13)变为如下广义被控对象:

其 中 -B1(t) =B2(t) =B(t),D12=(0 0 0 0 0 1)T,C2=diag{1,1,1,1,1,1}.取加权矩阵(这里矩阵退化为常数)R=5,C1=
当倒立摆两摆杆从静止下垂状态摆起到竖直倒立位置后,问题就转化成了平衡控制问题,这时相当于参考轨迹为x*=0,Δx=0-x=-x,那么广义被控对象(14)就转化为

其中当T=2.2s时,有

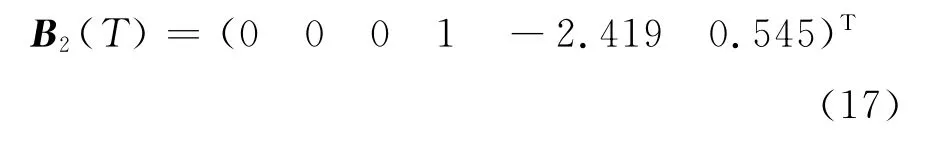
容易验证(A(T)B2(T))可控,(C2A(T))可观.通过迭代试算取γ=1.12,使得‖Tzw‖∞<γ,这里,Tzw为由w至z的闭环传递函数矩阵,即Tzw=(C1+D12K)(sI-A-B2K)-1B1,其中s为拉普拉斯算子,I为单位矩阵.求解如下代数黎卡提方程:
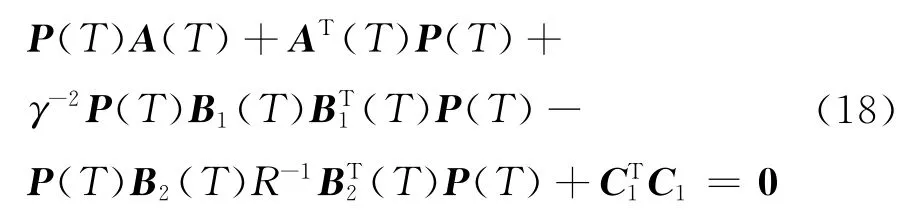
得到状态反馈矩阵
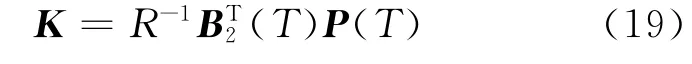
当γ→∞时,则得到的H∞反馈控制就是Q=时的LQR状态反馈控制,可以说H∞反馈控制是LQR控制的推广.因此,本文将H∞最优反馈控制推广到二级倒立摆自动摆起的轨迹跟踪控制中.针对广义被控对象(14),离线逆时间方向求解如下微分黎卡提方程:

其中初值条件(21)可以通过求方程(18)得到.于是得到反馈增益矩阵P(t),t∈ [0,T],从而有
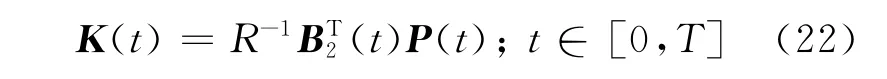
反馈增益矩阵K(t)随时间变化的曲线如图4所示.
于是,可以得到二级倒立摆系统自动摆起过程中的反馈控制如下:

考虑逆系统前馈控制(5)得到二级倒立摆系统自动摆起控制如下:
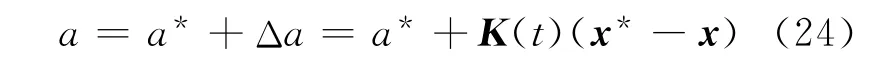

图4 反馈增益矩阵K(t)曲线Fig.4 The curves of feedback gain matrix K(t)
2.3 变增益H∞反馈控制器
两摆杆摆起到竖直位置后,需要进行稳定控制,这是一个无穷时间状态调节器问题.为此,本文设计了变增益H∞反馈控制器对二级倒立摆进行稳定控制.该控制器是一种新型的增益调度反馈控制器,在每个控制周期 (采样间隔)内,根据采样或者计算得到的系统状态值,把非线性系统线性化为线性定常系统,然后再针对这个线性定常系统构建H∞反馈控制器,在线求解代数黎卡提方程,得到随系统状态变化而变化的反馈增益矩阵,从而使得控制更为精确.
在二级倒立摆两摆杆处于竖直倒立位置的稳定控制过程中,受各种不确定因素的影响,系统的各状态变量不会完全收敛为零,而是在一定的范围内波动,因此该过程是一个受控稳定的过程.在这个过程中,位移x和摆角θi可以通过光电编码器获得,再利用差分方法就可得到和,记采样时刻的系统状态为,于是得到实时状态

根据二级倒立摆模型(2)~(4),可得系统的状态方程和输出方程
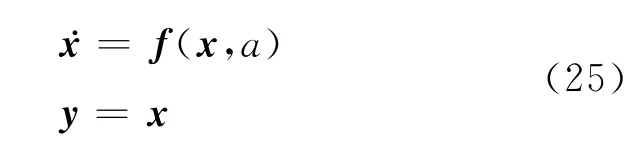
记

经过数学推导并舍去其中的高阶无穷小项,可以看出雅可比矩阵只与状态x有关,而与控制输入a无关.因此可以将A(x,a)、B(x,a)分别简记为A(x)、B(x).
在平衡点附近,系统(25)在采样点上的线性化方程为
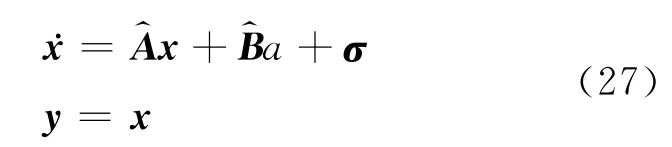
其中分别为雅可比矩阵

σ=为当前采样时刻的控制量.
当=0=0时,σ=0,方程(27)转化为平衡点上的线性系统

取可控性矩阵
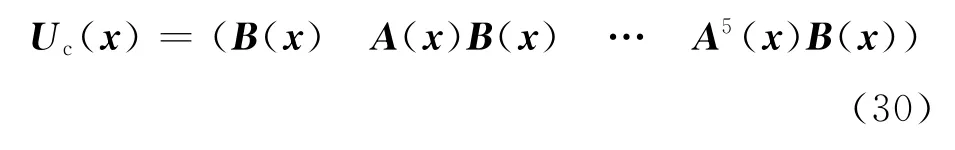
当x=0,即x=0,θi=0(i=1,2)时,有rank(Uc(x)|x=0)=6,因此,可知(AoBo)可控.为了方便,记平衡点的邻域为B(0,ε),根据可控性判据,当x∈B(0,ε)时,如果det(Uc(x))≠0,则rank(Uc(x)|x)=6,那么可得系数矩阵对(A(x)B(x))可控.通过计算发现det(Uc(x))与小车的位移无关,与摆角θ1、θ2有关.当x∈B(0,ε)时,det(Uc(x))与θ1、θ2之间的函数关系如图5所示.由图5可知,当∈B(0,ε)时,det(Uc(x))≠0,也就是说)可控.因此可以得到如下结论:如果系统在平衡点线性化的系数矩阵(AoBo)可控,那么当∈B(0,ε)时,基于采样点线性化的系数矩阵)也可控.

图5 平衡点附近det(Uc(x))与θ1、θ2 之间的函数关系Fig.5 The functional relationship between det(Uc(x))andθ1,θ2near the equilibrium point

即

令

得
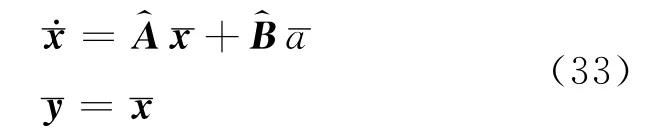
同样考虑到小车上的外界不确定干扰w,可以将方程(33)变为如下广义被控对象:


得到

由于反馈增益矩阵K随系统状态实时变化,该控制器具有比较强的自适应性和鲁棒性.
变增益H∞控制器的关键在于实时求解代数黎卡提方程(35).很多人讨论了黎卡提方程的求解方法[19~21],克莱曼迭代法和舒尔方法是目前广泛用于求解代数黎卡提方程的数值算法.大量的实时计算和数据存储是这些算法在实际应用中的主要障碍,本文基于舒尔方法设计了一个快速求解黎卡提方程的算法,用C语言代码编制程序,并在倒立摆的实物系统控制中应用成功.该算法主要包括以下过程:
(1)构造哈密顿矩阵;
(2)将哈密顿矩阵正交化为海森伯格形矩阵;
(3)采用双步隐式QR分解将矩阵化为实Schur形矩阵;
(4)对实Schur形矩阵进行复分解,将其化为严格上三角矩阵;
(5)根据正交变换矩阵得到代数黎卡提方程的解矩阵P,从而得到反馈增益K.
3 仿真结果
为了验证本文控制方案的有效性,利用Matlab进行了仿真实验.图6为二级倒立摆自动摆起控制的仿真曲线,其中a和x分别表示小车的控制量(加速度)、小车的速度和小车的实际位移分别表示小车加速度、小车速度和小车位移的参考轨迹分别表示摆角的输出轨迹和参考轨迹.仿真结果表明采用本文的控制方案能够实现对参考轨迹的精确跟踪,并在较短的时间内将两摆杆摆起到倒立位置.
实际上,由于实际系统存在测量误差、结构误差以及电气系统的输出误差等,倒立摆系统的数学模型与实际系统存在不可避免的偏差.因此,离线或者在线求得的控制数据与实际控制系统不可能完全匹配.为了验证本文控制方案的鲁棒性,在控制参数和数据不变的情况下,改变控制对象的物理参数来进行仿真,并在相同条件下与文献[10] 的控制方案进行了对比.

图6 二级倒立摆自动摆起控制的仿真曲线Fig.6 Simulation curves for the swing-up control of the double inverted pendulum
因为在系统建模时,摆杆的质心位置、转动惯量和轴承的摩擦因数这几个物理量的测量误差比较大,所以,下面的仿真实验中,假设质心位置、转动惯量、摩擦因数的误差分别为+5%、+10%、+10%(实际误差一般不会超过±5%).图中aLQR表示文献[10]中的控制方案(即逆系统前馈与基于LQR反馈控制相结合)中的控制量a,aH∞表示本文的控制方案(即逆系统前馈与基于H∞反馈控制相结合)中的控制量a,其他参数符号意义与此相同.如图7所示,在控制参数与实际系统有相当大的偏差时,本文的控制方案仍然能实现比较精确的轨迹跟踪,只有小车位移轨迹xH∞偏差较大,但仍能满足约束条件(8),精度优于xLQR.仿真结果表明本文的控制方案具有较好的鲁棒性.
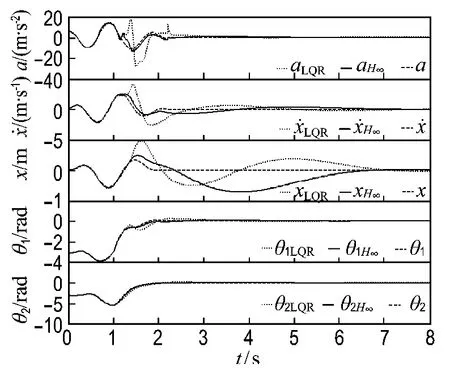
图7 具有模型偏差的仿真曲线Fig.7 Simulation curves of a deviation model
4 结 论
本文针对二级倒立摆自动摆起控制问题,通过离线求解常微分方程的两点边值问题,得到系统摆起的参考轨迹;设计了H∞增益调度反馈控制器以保证对摆起轨迹的精确跟踪和摆起控制的鲁棒性;此外,设计了变增益H∞反馈控制器使二级倒立摆的两个摆杆保持竖直倒立.变增益H∞反馈控制器的反馈增益随状态的变化而实时变化,因此从自动摆起到稳定控制过渡自然,不会引起系统的抖振.实验表明,该方案能够实现二级倒立摆的自动摆起,而且稳定性和鲁棒性明显提高.
[1] 张明廉,郝健康,何卫东.拟人智能控制与三级倒立摆[J].航空学报,1995,16(6):654-661
[2] 李德毅.三级倒立摆的云控制及动平衡模式[J].中国工程科学,1999,1(1):41-46
[3] KHALED G E,KUO C Y.Nonlinear optimal control of a triple link inverted pendulum with single control input[J].International Journal of Control,1998,69(2):239-256
[4] 李洪兴,苗志宏,王加银.四级倒立摆的变论域自适应模糊控制[J].中国科学(E辑),2002,32(1):65-75
[5] ASTR M K J,FRUTA K.Swinging up apendulum by energy control[J].Automatica,2000,36(2):287-295
[6] SPONG M W.Energy based control of a class of underactuated mechanical systems[C]//Thirteenth IFAC World Congress.San Francisco:IFAC,1996:431-435
[7] FANTONI I,LOZANO R,SPONG M W.Energy based control of the pendubot[J].IEEE Transactions on Automatic Control,2000,45(2):725-729
[8] YOSHIDA Kazunobu. Swing-up control of an inverted pendulum by energy based methods[C]//Proceedings of the American Control Conference.Piscataway:IEEE,1999:4045-4047
[9] 李祖枢,王育新,谭 智.小车二级摆系统的摆起倒立控制与实践 [C]//第五届全球智能控制与自动化大会会议论文集.杭州:浙江大学出版社,2004:2360-2364
[10] GRAICHEN K,TREUER M,ZEITZ M.Swing-up of the double pendulum on a cart by feed-forward and feedback control with experimental validation[J].Automatica,2007,43(1):63-71
[11] LIU T K,CHEN C H,LI Z S,etal.Method of inequali-based multi-objective genetic algorithm for optimizing a cart-double-pendulum system [J].International Journal of Automation and Computing,2009,6(1):29-37
[12] YANG J H,SHIM S Y,SEO J H,etal.Swing-up control for an inverted pendulum with restricted cart rail length [J].International Journal of Control,Automation,and Systems,2009,7(4):674-680
[13] 么健石,曾鹏鑫,徐心和.基于混合遗传算法的力矩受限圆轨二级倒立摆摆起控制[J].控制理论与应用,2005,22(4):615-618
[14] TAO C W,TAUR J,CHANG J H,etal.Adaptive fuzzy switched swing-up and sliding control for the double-pendulum-and-cart system[J].IEEE Transactions on Systems, Man,and Cybernetics— Part B:Cybernetics,2010,40(1):241-252
[15] GRAICHEN K,HAGENMEYER V,ZEITZ M.A new approach to inversion-based feedforward control design for nonlinear systems [J].Automatica,2005,41(12):2033-2041
[16] DEVASIA S,CHEN D,PADEN B.Nonlinear inversion-based output tracking [J]. IEEE Transactions on Automatic Control,1996,41(7):930-942
[17] LANE S H,STENGEL R F.Flight control design using nonlinear inverse dynamics[J].Automatica,1988,24(4):471-483
[18] 李春文,冯元琨.多变量非线性控制的逆系统方法[M].北京:清华大学出版社,1991
[19] KLEINMAN D L.On an iterative technique for Riccati equation computation[J].IEEE Transactions on Automatic Control,1968,AC-13(I):114-115
[20] LAUB A J.A Schur method for solving algebraic Riccati equations [J]. IEEE Transaction on Automatic Control,1979,24(6):913-921
[21] GRANAT R,KAGSTR M B,KRESSNER D.A parallel Schur method for solving continuous-time algebraic Riccati equations[C]//Proceedings of the IEEE International Symposium on Computer-Aided Control System Design.Piscataway:Institute of Electrical and Electronics Engineers Inc.,2008:583-588

