考虑交易对手违约相关的脆弱期权定价
陈 正 声, 秦 学 志
(1.大连理工大学 工商管理学院,辽宁 大连 116024;2.大连银行 风险管理部,辽宁 大连 116001)
0 引 言
脆弱期权(vulnerable option)为含有信用风险的金融衍生产品,即含有信用风险的期权,期权的卖方可能违约,从而可能导致期权得不到履行[1].金融交易过程中,大多数交易均在场外市场完成.场外交易的优点是合约的内容不受交易所限制,交易双方可以自由商谈达成对双方都有利的合约;缺点是会产生交易对手风险(也就是交易对手存在不履行合约的可能),而交易所内的交易几乎不可能触发对手信用风险.在金融市场上交易的场外期权,由于没有诸如清算中心等第三方的担保,均属脆弱期权,而类似于保险合约这样的众多合约同脆弱金融衍生工具面临着相同的问题.通常具有期权的支付形式,并且没有信用中介担保的私人合约均属于脆弱期权[1].另外,场外市场交易的期权会受到标的资产价值的变动和利率风险的影响,信用风险则随着期权交易对手方违约概率的变化而变化.2008~2009年美国华尔街金融危机的爆发再次说明,场外市场交易的衍生产品存在严重的潜在对手风险,而对场外衍生产品市场缺乏有效的监管使得一些信用衍生产品和证券化产品对金融危机的出现和扩散起到了推波助澜的作用.因此,准确定价在场外市场中交易的各类期权,对于有效抵御金融危机的发生并配合场外市场的监管有着重要的意义.
近年来,国外部分学者对相关问题进行了研究.文献[2~4]在简约化模型框架下,采用Cox过程对违约强度进行建模,并考虑了相关的衍生证券定价问题,但其模型忽视了交易对手风险因素的存在.Jarrow等[5]在上述简约化模型的基础上,提出了关于强度的违约相关模型,进一步从交易对手的角度完善和推广了先前的简约化模型.Leung等[6]在文献[5]工作的基础上,探讨了具有交易对手风险的CDS(信用违约互换)定价问题,但其忽视了利率风险的存在对交易双方违约强度的影响.Collin-Dufresne等[7]以简约化模型为基础采用了绝对连续的测度变换的方法对违约证券给出了一般性的定价公式,并对相关的衍生产品进行了实例研究.Johnson等[8]首次探讨了含有信用风险的期权定价问题,并引进脆弱期权这个术语定义含有交易对手违约风险的期权.Kang等[9]同样关注了Jarrow 等[5]的工作,将其方法应用于定价浮动利息票据(floating-rate notes)与脆弱期权,但其探讨的上述两个问题并没有考虑到交易对手间的环形违约相关情形.
本文在以上研究工作的基础上,考虑交易对手间信用风险状况的相互影响与市场风险因素共存时,脆弱欧式期权的定价问题.
1 模 型
考虑在市场风险因素影响下,构建两个公司(B、C)间违约强度模型.刻画公司B违约时间的随机变量记为τB,公司C违约时间的随机变量记为表示公司i的违约示性函数:在发生违约时公司i的示性函数的值为1,否则为0.在概率空间上,存在用来描述无违约期限结构变化的经济状态变量Xt,如利率rt.
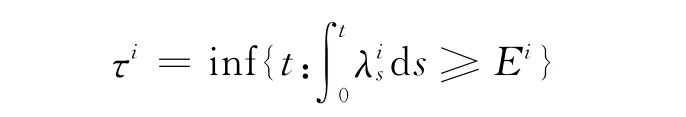
式中:Ei表示相互独立的单位指数随机变量表示强度过程.因此,公司i的条件存活概率,即违约时间τi的分布为

对于期限为T的风险折现债券D(t,T),设τ为违约时间,R为违约时的回收率,由文献[2、3]知,t时刻债券的价格为

由文献[2、5]有
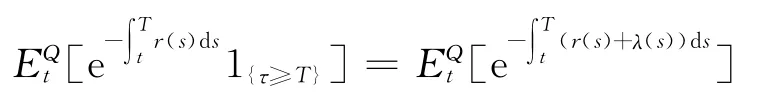
到期日支付为Z的风险债券价格为
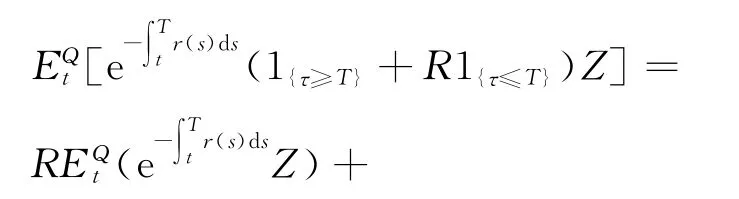

Ong[10]指出:“度量信用风险的完美模型应该包含交易对手风险和市场风险因素,对于违约强度的建模同时应考虑市场风险因素.”因此,本文考虑当交易对手风险与市场风险因素共存时,违约强度模型的构造.针对存在交易对手关系的公司B、C,若公司B的违约概率很大程度上受到公司C的影响,另外,如果公司C又持有公司B发行的大量债券,此时便形成了环形违约相关情形,两公司B、C的信用状况对其间违约相关性的影响至关重要,其实质为两公司间违约强度的相互影响,具体表现为违约时强度表现出的跳跃.则关于公司B与C的违约强度模型:
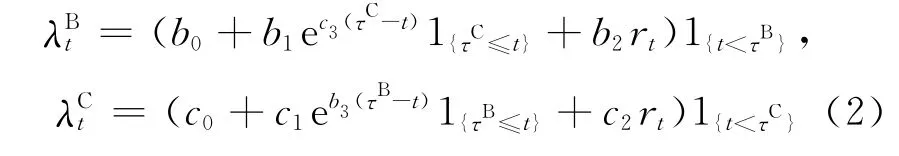

其中α、β、σ均为正数,W1(t)为维纳过程.随机微分方程(3)的闭式解为

设V(t,T)为在T时刻具有1美元收益的无违约折现债券在t时刻的价格,由 Vasicek[11]与Shreve[12]的结论,有

其中
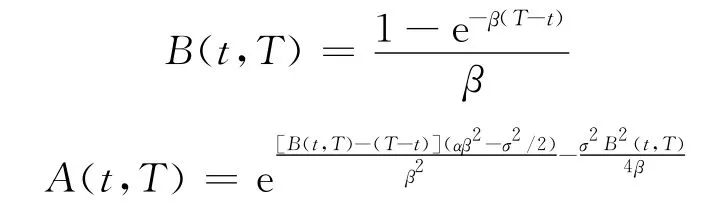
命题1 违约强度模型满足式(2)时,违约时间随机向量(τBτC)∈ [0,T]×[0,T]的联合违约密度函数f(t1,t2)为

证明 设公司B与C的违约时间随机向量(τBτC)的联合违约概率密度函数为f(t1,t2).在此采用由文献[7]中提出的测度变换方法,对联合违约密度函数进行计算,定义测度变换为

其中Pi(i=B,C)为新的概率测度,在[0,τi]上关于Q绝对连续,在[τi,+∞)上几乎处处为0.在新的测度Pi下,EB、EC分别为测度PB、PC下的期望,违约强度分别记为由以上结论,在t1>t2时得到
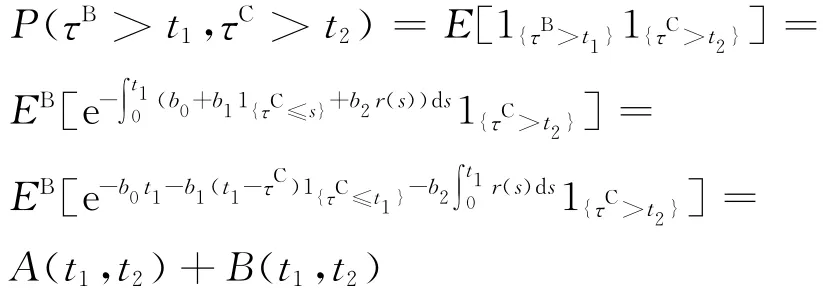
其中
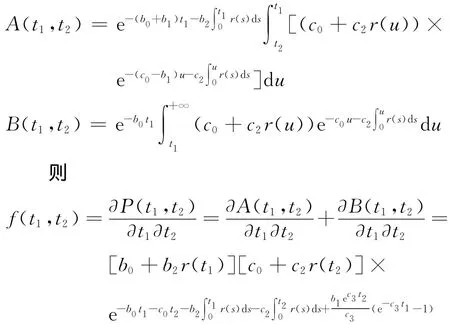
同理得到t1≤t2时,f(t1,t2)的表达式.故命题成立.
2 脆弱欧式看涨期权的定价
2.1 模型的建立
Johnson等[8]和 Klein等[13、14]分别探讨 了含有信用风险的期权定价问题.本节采用文献[13、14]中提出、在文献[9]中应用的含有交易对手风险的脆弱期权定价公式,并在Kang等[9]采用的文献[5]提出的违约强度模型的基础上,考虑期权的持有者同期权的开立者之间形成的环形违约相关情形.
采用非线性环形违约强度模型式(2),其中公司B为期权的持有者,公司C为期权的开立者,公司B的违约强度同公司C及利率相关.
在等价鞅测度Q下,脆弱欧式看涨期权的标的资产的价格S(t)服从

其中W2(t)为标准的维纳过程,利率rt满足式(3),并且协方差cov(σSdW2,σdW1)=ωσσSdt,σ、σS、ω均为正常数.由式(1)知,脆弱欧式看涨期权在时刻t的价格为

其中S(T)为标的资产到期时的价格,K为执行价格.得到如下命题.
命题2 设标的资产的价格S(t)服从式(4),利率 服 从 式 (3),且 满 足 cov(σSdW2,σdW1)=ωσσSdt,其中σ、σS、ω均为正常数.违约强度模型取为式(2).则在交易对手违约相关及市场风险因素共同作用下,脆弱欧式看涨期权价格为

其中R为回收率,N(·)为标准正态分布函数,


证明 设公司B为期权的持有者,公司C为开立者,由命题1得到,违约时刻的随机向量(τBτC)∈ [0,T]×[0,T]的联合违约密度函数为f(t1,t2).
对于式(6)的计算,首先

进一步得到

由利率rt满足的随机微分方程(3)的显式解得到

2.2 定价结果对比分析
为同文献[9]中的结果进行比较,本文采用文献[9]中参数的设置,即对于脆弱期权的持有者公司B,其违约强度表达式中的参数取为b0=0.038,b1=0.5,b2=-0.1.并取c1=0.5,c2=-0.1,α=0.04,β=0.8,σ=0.03,ω=0.6,T-t=0.5,利率的初值为r0=0.04.经过数值计算得到的结果见表1~3.

表1 对应不同回收率的脆弱欧式看涨期权价格(S=100,K=90)Tab.1 The price of vulnerable European call option for different recovery rate(S=100,K=90)

表2 对应不同回收率的脆弱欧式看涨期权价格(S=100,K=100)Tab.2 The price of vulnerable European call option for different recovery rate(S=100,K=100)

表3 对应不同回收率的脆弱欧式看涨期权价格(S=100,K=110)Tab.3 The price of vulnerable European call option for different recovery rate(S=100,K=110)
分别对脆弱期权的实值、平值和虚值3种状态进行比较.从表1~3的对比结果发现,对于给定的回收率,由于环形违约相关的存在,随着期权卖方违约概率的增加,脆弱期权的价格逐渐降低,这一点同文献[9]的结果相一致.本文模型得到的脆弱期权的价格要低于文献[9]的对应价格,表明采用了非线性环形违约强度模型式(2)的期权定价模型揭示出合约蕴含着更高的违约风险.另外,由表1~3可见,对于不同的回收率,采用非线性环形违约强度模型式(2)的定价模型对脆弱期权价格的影响要强于文献[9]中的定价模型(对于回收率的不同取值,其定价模型的结果仅以0.001或0.01为单位变化,而本文模型结果以1或0.1为单位变化),说明本文模型对于回收率的敏感性要强于文献[9]中的模型.
表4中回收率R=0.6.由分析结果可以看到:在给定对手方的违约概率时,随着标的资产收益率的波动率的增加,脆弱欧式看涨期权的价格逐渐增加;在给定波动率时,随着对手方违约概率的增加,脆弱期权的价格逐渐降低.由此可知,当标的资产的收益率的波动率上升时,脆弱欧式看涨期权的价格上升,但脆弱期权的持有者在到期前还面临着卖方形成的信用风险,使得随着违约风险的逐渐提升,脆弱期权的价格将逐渐降低.
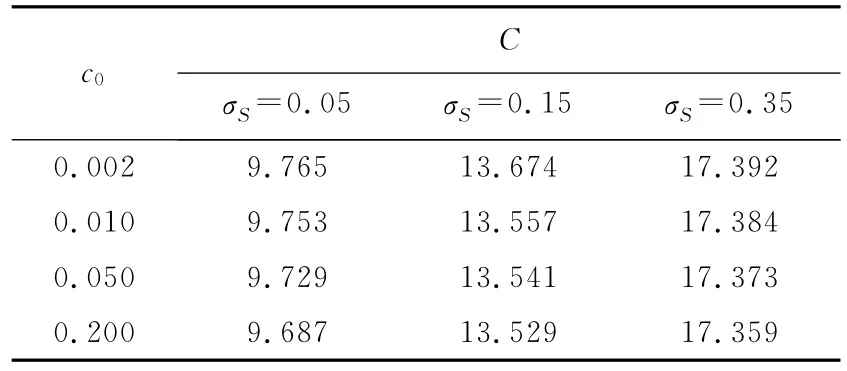
表4 对应不同标的资产波动率的脆弱欧式看涨期权价格Tab.4 The price of vulnerable European call option for different volatility of underlying asset
表5中回收率R=0.6.从结果可以看到,对于给定的回收率与相关系数,随着期权开立者违约概率的增加,脆弱期权的价格逐渐降低.相关系数的绝对值越大,则利率与标的资产间的相互影响就越大.从其变化趋势可知,对于给定对手方的违约概率,随着利率与标的资产间变化趋势的同向性逐渐增强,脆弱欧式看涨期权的价格将逐渐升高.

表5 对应不同相关系数的脆弱欧式看涨期权价格Tab.5 The price of vulnerable European call option for different correlation coefficients
3 结 语
金融危机在全球范围内的传导和肆虐,一再警示了信用违约相关度量及风险传导机理甄别的重要性.本文在设定违约强度同市场风险因素相关的情形下,考察了含有交易对手违约风险的脆弱欧式看涨期权定价问题.采用简约化模型对脆弱欧式看涨期权的定价进行了研究,定价结果对比分析表明:本文提出的非线性环形违约强度模型揭示了交易对手间信用状况的相互作用对定价结果的影响,并可作为研究违约相关问题的一种有效方法.另外,此次金融危机也暴露出与金融衍生产品的定价和交易过程相伴随的严重的信息不对称问题,其对金融衍生品定价和风险管理的影响将成为下一步的研究内容.
[1] COSSIN D,PRRIOTTE H.高级信用风险分析[M].殷剑峰,王唯翔,程 炼,等译.北京:机械工业出版社,2005
[2] LANDO D.On Cox processes and credit risky securities[J].Review of Derivatives Research,1998,11(2):99-120
[3] LANDO D.Three essays on contingent claims pricing[D].New York:Cornell University,1997
[4] DUFFIE D, SINGLETON K. Modeling term structures of defaultable bonds [J].Review of Financial Studies,1999,12(4):687-720
[5] JARROW R A,YU F.Counterparty risk and the pricing of defaultable securities [J].Journal of Finance,2001,56(5):1765-1799
[6] LEUNG S Y,KWOK Y K.Credit default swap valuation with counterparty risk[J].Kyoto Economic Review,2005,74(1):25-45
[7] COLLIN-DUFRESNE P, GOLDSTEIN R S,HUGONNIER J.A general formula for valuing defaultable securities [J].Econometrica,2004,72(5):1377-1407
[8] JOHNSON H,STULZ R.The pricing of options with default risk [J].Journal of Finance,1987,XLII(2):267-280
[9] KANG J,KIM H S.Pricing counterparty default risks:Applications to FRN and vulnerable options[J].International Review of Financial Analysis,2005,14(3):376-392
[10] ONG M K.内部信用风险模型 [M].李志辉,译.天津:南开大学出版社,2005
[11] VASICEK O.An equilibrium characterization of the term structure[J].Journal of Financial Economics,1977,5(2):177-188
[12] SHREVE S E.Stochastic Calculus for Finance II[M].New York:Springer,2004
[13] KLEIN P. Pricing Black-Scholes options with correlated credit risk [J].Journal of Banking and Finance,1996,20(7):1211-1229
[14] KLEIN P,INGLIS M.Valuation of European options subject to financial distress and interest rate risk[J].The Journal of Derivatives,1999,6(3):44-56
[15] RICHARD L,DOUGLAS J.Numerical Analysis[M].7版.冯烟利,朱海燕,译.北京:高等教育出版社,2005
[16] MUSIELA M, RUTKOWSKI M. Martingale Methods in Financial Modeling [M].New York:Springer-Verlag,1997

