基于软迭代的叠加训练序列信道估计方法

邢 慧 玲， 魏 东 兴， 殷 福 亮

（大连理工大学 信息与通信工程学院，辽宁 大连 116024）

0 引 言

信道估计是无线通信系统的关键技术，相关检测和相干解调等算法都需要已知信道状态信息（channel state information，CSI），因此 CSI的估计精度直接影响到接收机的性能.实际的通信系统通常采用基于训练序列的信道估计方法，该方法将训练序列和信息序列时分复用或频分复用后再进行发送，这样可以获得较准确的信道估计.但该类方法的主要缺点是降低了信息速率，浪费了信道资源，特别是在快时变信道中，为了能够跟踪信道变化，训练序列更需要频繁的发送，导致信道利用率严重下降.信道估计的另一类方法是盲信道估计，该类方法不需要使用训练序列，但也存在一些缺陷，比如利用循环平稳信号二阶统计量的盲信道估计方法对非最小相位信道存在相位不确定性[1]，而基于高阶统计量的方法计算复杂度高，难以实现实时处理等[2].

为了使信道估计方法复杂度低且信道利用率高，近年来人们提出了一种将训练序列叠加在信息序列上一起发送的方法，即叠加训练序列信道估计[3～10]方法.如文献[4]针对单输入单输出信道提出了一种叠加训练序列信道估计方法，该方法在发送端将周期的训练序列与信息序列进行算术叠加后一起发送，在接收端将接收序列分块叠加，由于一阶统计量中未知信息相互抵消，而已知训练序列同相叠加增强，可以获得低复杂度的信道估计.由于叠加训练序列不占用专门的时隙，该方法提高了信道利用率；此外，该方法仅需计算一阶统计量，比盲估计方法计算复杂度低，且不需要严格的识别条件.文献[5]将该方法扩展至单输入多输出信道以及时变信道；文献[6]给出了多输入多输出信道下的叠加训练序列信道估计方法，并利用基于确定性最大似然的信道与字符联合迭代估计来提高信道估计精度.上述叠加训练序列信道估计方法通常假设信息序列是零均值的，即在信道估计时忽略了一阶统计量中来自信息序列的干扰.但是，由于在分块叠加时序列长度有限，无法完全消除未知信息序列干扰，为了进一步提高估计精度，需要在估计前进行干扰消除.文献[7]提出了一种块传输方案，通过预失真处理，使得信息序列在训练序列的所有频率分量处没有能量分布，由此提高了信道估计的精度.软迭代的信道估计就是要利用信道译码器输出的软信息，将其反馈给信道估计器进行判决指向的参数估计[11]，该方法适用于近容量的迭代接收机结构，在改善信道估计精度的同时能够使系统接近最优的检测性能.文献[10]提出了一种应用于比特交织编码调制系统的软迭代信道估计方法，该方法利用叠加训练序列为迭代信道估计器提供信道参数的初值，再利用Kalman滤波方法对快衰落信道进行跟踪.

本文提出一种基于软迭代的叠加训练序列信道估计方法，即使用一阶统计量进行信道估计，降低计算复杂度，另外利用译码器输出的软信息进行干扰消除以获得较好的估计性能.该方法的一次迭代过程如下：首先利用文献[5]提出的叠加训练序列信道估计方法来获得信道参数估计的初值，接收机用该信道参数进行第一次迭代检测，将软输入软输出（soft－input soft－output，SISO）译码器输出的软信息送入叠加训练序列信道估计器，用它来消除观测量中来自未知信息的干扰，由此获得更精确的信道参数估计值；然后，将修正的信道参数反馈给迭代接收机，重新对接收序列进行均衡以及译码；最后使SISO译码器输出更可靠的软判决信息.

1 基于一阶统计量的叠加训练序列信道估计方法

假设离散时间频率选择性衰落信道的冲激响应序列为h＝｛h（l）｝，零均值的信道高斯噪声为v（n），发射机输出序列为s（n），对信道输出进行码元速率采样可得

式中：L为信道阶数.假设训练序列c（n）的周期为P，即c（n）＝c（n＋mP），零均值的独立同分布信息序列为b（n），将训练序列c（n）直接叠加到调制器的输出b（n）上，则有

由于c（n）是周期序列，其循环频率分量可表示为

则周期训练序列c（n）可表示为

其中αm＝2m/P.由于循环频率分量cm在接收端是已知的，且E[b（n）]＝0，则接收序列y（n）的一阶统计量可以表示为

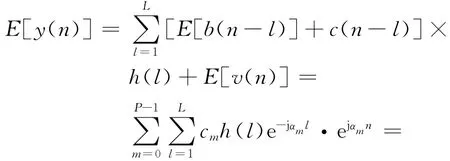
其中

当序列长度N较大时，可以用接收序列y（n）的时间平均来近似统计平均，此时gm可以近似表示为[4]

由于循环频率分量c1，c2，…，cP在接收端已知，根据式（6），循环频率分量矩阵可以写成C＝diag｛c1，c2，…，cP｝·Ω，其中矩阵Ω可以表示为

则式（6）的矩阵表示形式为

于是，频率选择性衰落信道参数h的无偏估计为[5]

2 基于软迭代的叠加训练序列信道估计方法

由上面的估计步骤可知，叠加训练序列方法假设信息序列的均值为零，即忽略了一阶统计观测量中来自未知信息的干扰.但是，由式（5）和（7）可知，在估计过程中由于数据长度N有限，用于信道估计的观测量gm中除了噪声之外，还存在来自信息的干扰分量.因此为了进一步提高估计精度，需要消除来自信息的干扰分量.本文提出了基于软迭代的叠加训练序列信道估计方法，利用软输出译码器输出的先验信息来消除信息干扰，由此提高信道估计的精度.该方法需要结合软输出译码器来实现，因此适合应用于迭代接收机结构.

Turbo均衡接收机是典型的迭代接收机结构，在其工作过程中，均衡器与信道译码器通过交换各自的软信息进行迭代接收，这样可以获得较低的误码率.本文将提出的信道估计方法应用于Turbo均衡接收机，通过提高信道参数的估计精度，进一步改善接收机性能.Turbo均衡接收机结构如图1所示，它由以下模块组成：软输入的叠加训练序列信道估计器、SISO信道均衡器以及SISO卷积码译码器，译码器与均衡器之间采用交织器和解交织器相连[9].

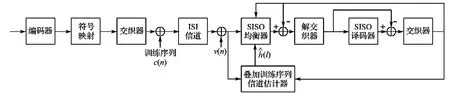
图1 采用软迭代信道估计的Turbo均衡接收机结构Fig.1 Turbo equalizer with soft－iterative channel estimator

软迭代叠加训练序列信道估计算法步骤归纳如下：

（1）初始化

（2）迭代计算

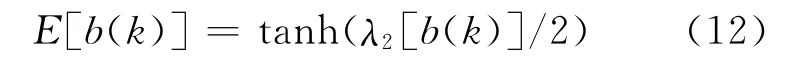
将式（12）的计算结果反馈给信道估计器，用来消除接收序列一阶统计量中的信息干扰，则将式（7）修正为

将修正后的gm重新代入式（10）计算新的信道参数

（3）迭代终止

与第1章的非迭代叠加训练估计方法相比，软迭代信道估计方法采用了干扰消除方案，利用信道编码器输出的软信息计算出信息序列的一阶统计量，然后反馈给信道估计器进行干扰消除，从而使信道估计性能得到改善.

3 仿真结果与分析

为了验证本文方法的有效性，对算法进行了计算机仿真实验.为了简单起见，发送信息序列采用BPSK调制方式，信道编码采用码率为1/2的卷积码，其生成多项式为g1＝ [1 1 1]，g2＝[1 0 1].使用文献[5]中的最优周期训练序列1.02｝，其周期为6.信道为频率选择性块衰落信道，信道建模采用抽头延迟线模型，仿真中采用三径实信道模型，信道参数为h＝ （0.407 0.815 0.407）.数据帧长度N＝Np·6，其中Np为整数.训练序列和信息序列的平均功率分别表示为定义功率分配因子本文中SISO均衡器和译码器均采用最大后验概率（maximum a posteriori，MAP）译码算法.

在信噪比（signal－noise ratio，Rsn）从0到20 dB的区间内，选取Tir＝1，Np＝24，即数据帧长度为144.在训练序列与信息序列平均功率相等的情况下，对信道估计的性能进行仿真.这里用归一化均方误差Enms来评价信道估计性能.

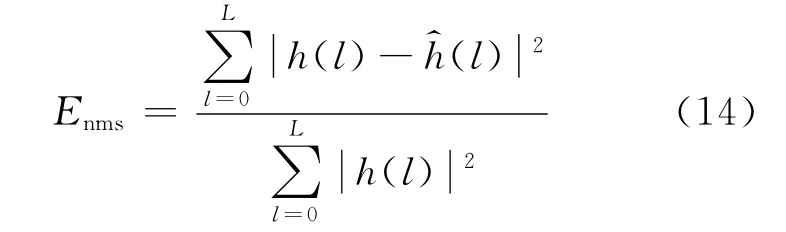
经过500次Monte Carlo仿真，本文的软迭代叠加训练序列信道估计方法与非软迭代方法的信道估计性能比较如图2所示.从图2可以看出，随着信噪比的提高，非迭代叠加训练序列估计误差下降较慢，在Enms＝10－2左右会出现差错平层.而软迭代方法由于消除了信息序列的干扰，能够有效地改善信道估计的性能，仅迭代1次就使估计精度获得了较大提高.在中高信噪比情况下，软迭代方法比非迭代方法估计误差下降了1～2个数量级.随着迭代次数的增加，估计误差会进一步降低，但下降的幅度较小.由图2可见，迭代3次的估计性能与迭代2次的估计性能相近.因此，本文的软迭代信道估计方法迭代2次后，信道估计基本收敛.

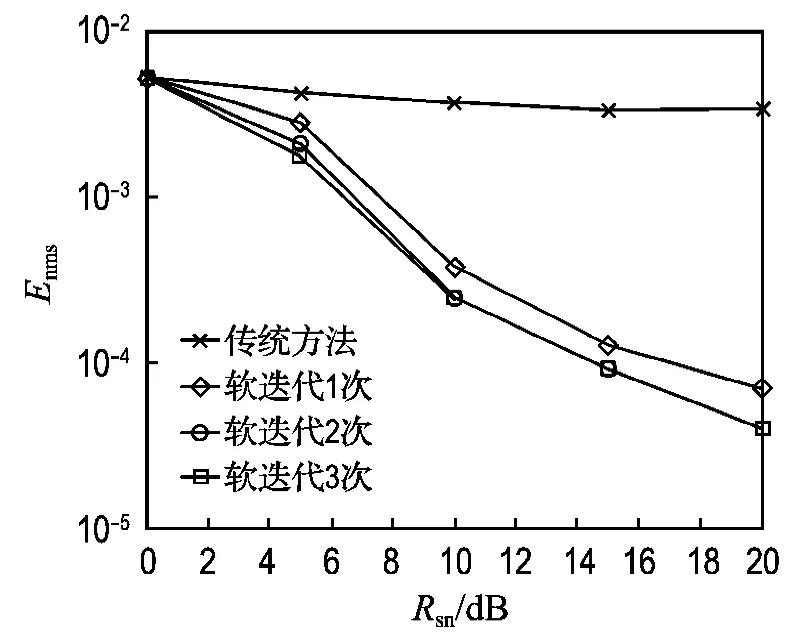
图2 信道估计性能比较Fig.2 Comparisons of channel estimation performance

由于叠加训练序列会造成发射功率的浪费，参数Tir的选择直接影响着系统的功率利用率和估计精度这两个主要性能，本文分别对Tir＝1的非迭代方法、Tir分别等于0.20和0.67的1次软迭代方法的信道估计性能进行了仿真，仿真结果如图3所示.仿真结果表明，在低信噪比情况下，由于一阶统计量估计算法自身的局限，叠加功率较低的训练序列会导致较差的估计性能；但在中高信噪比情况下，将Tir＝1的非迭代方法与Tir＝0.20的1次软迭代方法进行比较，可以看出，软迭代方法在相同估计性能的前提下可以明显地节省发射功率.实验结果表明，在Enms＝10－2左右，软迭代方法可以使功率降低7dB左右.

选取参数Tir＝1，Np＝24，对采用软迭代叠加训练序列信道估计的Turbo均衡接收机的误码率性能进行500次Monte Carlo仿真，结果如图4所示.由图4可见，由于软迭代的信道估计器将修正的信道参数送入SISO均衡器，系统的误码率（bit error rate，Rbe）性能得到明显的改善，在误码率为10－3的条件下，迭代1次可以获得2dB以上的信噪比增益，迭代2次可以获得3dB以上的信噪比增益.此外，估计精度的提高，进一步加快了Turbo均衡接收机的收敛速度，仅需迭代2次，接收机即可获得良好的误码率性能.

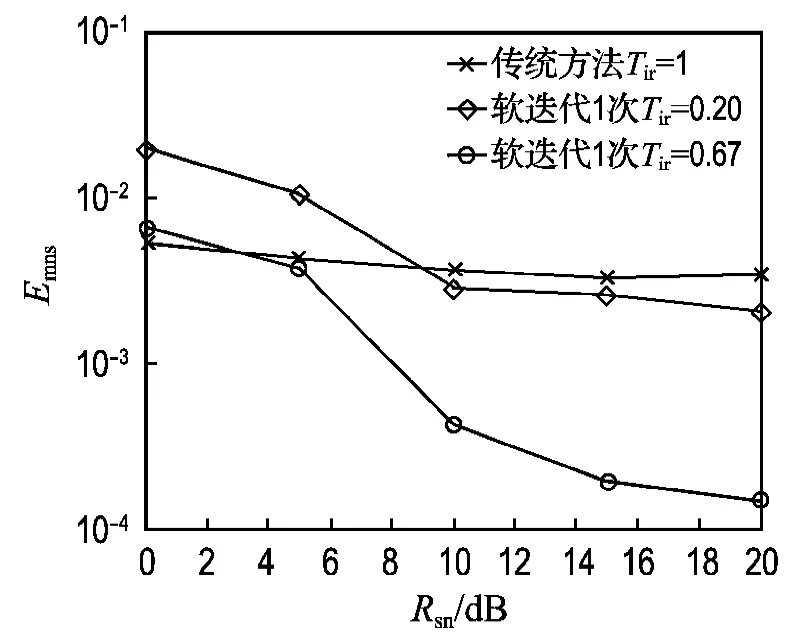
图3 不同功率比值下信道估计性能的比较Fig.3 Comparisons of channel estimation performance with different power ratios

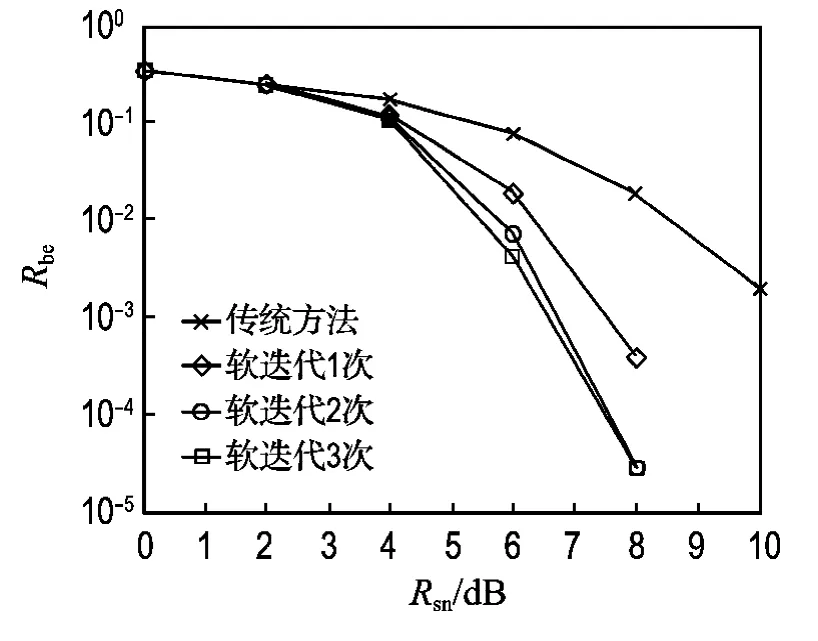
图4 采用软迭代信道估计的Turbo均衡接收机误码率性能Fig.4 Bit error rate performance of Turbo equalizer with soft－iterative channel estimation

4 结 论

本文给出了一种基于软迭代的叠加训练序列信道估计方法.该方法利用信道译码器输出的软信息来消除接收序列一阶统计量中的信息残余，在没有带宽损失的情况下进一步提高了信道估计的精度，在中高信噪比区域，仅需迭代1次就使信道估计误差降低了1～2个数量级.此外，该方法计算复杂度较小，可以适当地降低发射功率，适用于在迭代接收机结构中进一步改善系统性能.

[1] TONG Lang， PERREAU S. Blind channel estimation：from subspace to maximum likelihood methods [J].Proceedings of the IEEE，1998，86（10）：1951－1968

[2] GIANNAKIS G B， HUA Y.Signal Processing Advances in Wireless and Mobile Communications：Trend in Channel Estimation and Equalization[M].London：Prentice－Hall，2001

[3] FRAHANG－BOROUJENY B. Pilot－based channel identification：proposal for semi－blind identification of communications channels [J].Electronics Letters，1995，31（13）：1044－1046

[4] ZHOU G T，VIBERG M，MCKELVEY T.A firstorder statistical method for channel estimation [J].IEEE Signal Processing Letters，2003，10（3）：57－60

[5] TUGNAIT J K，LUO W.On channel estimation using superimposed training and first－order statistics[J].IEEE Communications Letters，2003，7（9）：413－415

[6] MENG X， TUGNAIT J K. MIMO channel estimation using superimposed training[C]//IEEE ICC 2004：2004IEEE International Conference on Communications.Paris：IEEE，2004

[7] GHOGHO M，MCLERNON D.Channel estimation and symbol detection for block transmission using data－dependent superimposed training [J].IEEE Signal Processing Letters，2005，12（3）：226－229

[8] OROZCO－LUGO A G，LARA M M，MCLERNON D C.Channel estimation using implicit training[J].IEEE Transactions on Signal Processing，2004，52（1）：240－254

[9] TUGNAIT J K， MENG Xiao－hong. On superimposed training for channel estimation：performance analysis，training power allocation，and frame synchronization [J].IEEE Transactions on Signal Processing，2006，54（2）：752－765

[10] ANDALIBI Z，NGUYEN H H，SALT J E.Softiterative channel estimator for BICM－ID－SSD over time－varying flat fading channels[C]//WTS 2009：Wireless Telecommunications Symposium 2009.Prague：IEEE，2009

[11] NICOLI M，SFERRARA S，SPGNOLINI U.Softiterative channel estimation：method and performance analysis [J]. IEEE Transactions on Signal Processing，2007，55（6）：240－254