Lévy过程驱动金融市场中最优资产组合复制策略

王 岩， 冯 敬 海， 冯 恩 民

（大连理工大学 数学科学学院，辽宁 大连 116024）

0 引 言

计算欧式期权的对冲策略，即找到一个资产组合，使资产组合复制的财富过程能够模拟期权的价值.因此找到满足一定条件的最优资产组合是金融研究中的一类重要问题.文献[1]论述了最优资产组合可以通过期权价格的鞅表示定理——Clark－Haussmann－Ocone（CHO）定理得到.

近年来，随着白噪声分析理论的发展，它在金融中的应用也受到了广泛的关注.白噪声分析是由Hida[2]首创的无穷维随机分析，是一种无穷维的Schwartz型分布理论.Aase等[3]将CHO定理分别推广到Gauss白噪声分析和Poisson白噪声分析框架下，用于研究布朗运动和Poisson过程驱动的金融市场，用Malliavin导数表示欧式期权的最优复制策略.布朗运动驱动的金融市场和Poisson过程驱动的金融市场是两个经典的分别存在着连续型和跳跃型随机因素的市场.

文献[3]的思想和结果随后被推广到更一般的随机过程驱动的金融市场，如文献[4、5].随着在理论和应用方面的蓬勃发展，Lévy过程已经成为概率论的最热门分支之一.用Lévy过程建立金融市场模型，尤其在描述股票的价格方面，更为贴切[6～9].Lévy过程可以分解为时间变量、布朗运动和纯跳Lévy过程的线性组合[10]，因此布朗运动和Poisson过程都是Lévy过程的特例.L kka等[11]首次构建纯跳 Lévy白噪声分析框架，并应用于随机微分方程的求解.文献[12]在文献[11]的框架下，求解纯跳Lévy白噪声驱动的随机薛定谔方程.L kka[13]利用白噪声分析理论推导了纯跳Lévy过程的CHO定理，用于研究Lévy过程驱动的金融市场的对冲问题.随后，Di Nunno等[14]进一步构建了纯跳Lévy过程的白噪声分析框架，引入Malliavin导数，将CHO定理推广到纯跳Lévy过程的白噪声分析框架下，用于求解纯跳Lévy过程驱动的金融市场中欧式期权的最优复制策略.

本文研究由布朗运动和纯跳Lévy过程复合的Lévy过程驱动的金融市场.此市场既有连续波动的性质，又复合了如金融危机等重大金融事件所造成的不规则跳跃式波动，更切近现实中一般的市场，是文献[3、14]中模型的一般化和复杂化.Lévy白噪声可视为Lévy过程的广义时间导数，因此本文研究的Lévy白噪声是Gauss白噪声和纯跳Lévy白噪声的复合.文献[15]构建了相应的Lévy白噪声分析框架，本文将CHO定理推广到Lévy白噪声分析框架下，用Malliavin导数表示市场中的方差最小资产组合，并研究Lévy过程驱动的金融市场的固有风险.

1 Lévy白噪声分析框架下的Clark－Haussmann－Ocone定理

令（Ω，F，P）为完备的概率空间，｛Ft｝t≥0为其上的滤子.Lévy过程η（t）＝η（t，ω）：[0，∞）×Ω→R为一个平稳独立增量过程，η（0）＝0，且满足E[η2（t）]＜∞，对t≥0都成立.令Δη（t）表示η在t时刻的跳跃，令假 设则变换后的也为一个 Lévy过程[16].

可选取一列实数ai，j，使得为强正交鞅[16].根据Lévy－It分解定理[10]，Lévy过程η（t）可以分解为

其中a∈R，σ∈R，B（t）为布朗运动，（dt，dz）＝N（dt，dz）－ν（dz）dt为补偿 Poisson随机测度，N（dt，dz）为η（t）的Poisson随机测度，ν（dz）为η（t）的Lévy测度，B（t）与dt，dz）独立.

此市场既有连续型的随机因素，又复合了如金融危机等重大金融事件所造成的不规则跳跃式波动.

Lévy白噪声可视为Lévy过程的广义时间导数，本文研究的Lévy白噪声是Gauss白噪声和纯跳Lévy白噪声的复合.文献[15]构建了Lévy白噪声分析框架.

令S（Rd）为Rd上的C∞全体速降函数所组成的Schwartz空间，S′（Rd）为S（Rd）的对偶空间，μG是定义在S′（Rd）空间上的Gauss白噪声测度.令（X）为S（Rd＋1）的商空间，X＝Rd×R0，（X）为（X）的对偶空间，μp是定义在（X）上的纯跳Lévy白噪声测度.因为本文研究的Lévy白噪声的噪声源是二维的——Gauss白噪声和纯跳Lévy白噪声，故令空间Ω＝S′（Rd）×S′（X），θ＝μG×μp.

定义2 令B（Ω）为Borelσ代数，定义（Ω，B（Ω），θ）为Lévy白噪声空间，θ＝μG×μp为Lévy白噪声测度.

引理1[15]令α＝ （α1，α2，…）为多维数组，有限个αi非0，且表 示 多 维 数 组α＝ （α1，α2，…） 的 集 合. 令｛Hα（ω）｝α∈J和｛Kβ（ω）｝β∈J分别为平方可积的白噪声泛函空间L2（μG）和L2（μp）中的混沌分解基.则对平方可积的Lévy白噪声泛函f∈L2（θ），存在着空间L2（θ）中的一组混沌分解基｛Mγ｝γ∈T，使 得 其 中Mγ（ω1，ω2）＝Hα（ω1）Kβ（ω2），T＝J×J，α，β∈J，γ＝ （αβ）∈T，ω1∈S′（Rd），ω2∈（X），Cγ＝（aα，bβ），且有

为了定义f∈L2（θ）在t点对于Gauss型随机元素ω1∈S′（Rd）和纯跳 Lévy型随机元素ω2∈（X）的Malliavin导数，首先给出分布空间的定义，Malliavin导数定义在此随机分布空间上.

定义3 令q∈Z，对平方可积的Gauss白噪声泛函定义范数，定义随机分布空间为并在上配备归纳极限拓扑.另一方面，令q∈Z，对平方可积的纯跳Lévy白噪声泛函， 定 义 范 数令

定义4 对Lévy白噪声泛函f（ω）＝f（ω1，

根据定义3，存在着包含关系L2（θ）

定义在t点关于ω2的Malliavin导数为

这里ξi（t）为 Hermite函数0 … 0），l（i，m）＝m＋ （i＋m－2）（i＋m－1）/2.

下面给出L2（θ）上的CHO定理，此定理的证明是文献[3]中定理3.11和文献[14]中定理4.12的平行推广，在此不再重复.

定理1 （L2（θ）上的CHO定理）令λ表示R上的Lebesgue测度，f∈L2（θ）为FT可测的，则有L2（λθ），并且

这里E为广义期望表示F在t点关于ω1的Malliavin导数表示F在t点关于ω2的Malliavin导数，是Lévy过程η（t）的正交幂跳过程，Y（1）（t）＝η（t），且当m≠n时，Y（m）（t）和Y（n）（t）是正交的.

2 Lévy过程驱动的金融市场模型

本文研究由一种无风险资产S0（t）和K（K＜ ∞）种风险资产S1（t），…，SK（t）组成的金融市场，交割日期为T.市场是由Lévy过程驱动的，即风险资产由Lévy过程来刻画.为了简化计算，可以将标的资产的价值表示为

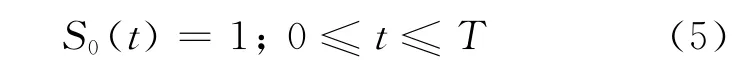
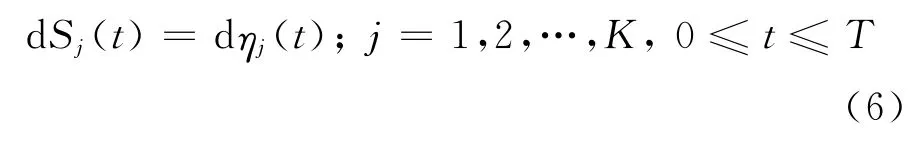
本文讨论如何选择资产组合复制欧式期权F∈L2（θ）的价值，θ为Lévy白噪声测度.在金融模型中有一个信息滤子流｛Ft｝，刻画在每个时间点投资者所能获取的信息总量.通常假设这个信息滤子流与风险资产价格过程生成的信息相一致，即假设资产组合过程是信息滤子流｛Ft｝适应的，称｛Ft｝t∈[0，T]所承载的信息为完全信息.对于投资者来说，通常在决策时所获取的信息是不完全的，即存在着一族子σ－代数｛Ht｝t∈[0，T]表示在t时刻可以获取的信息集，对于t∈[0，T]，有HtFt.称｛Ht｝t∈[0，T]所承载的信息为部分信息.

例1φ（t）∈Ht＝F（t－δ）＋，δ＞0为常数，表示信息流存在着δ时间的延迟，即投资者要在tδ这一时刻，参照F（t－δ）＋所包含的信息，决定t时刻的随机过程φ（t）的取值.

定义5 令φ（t） ＝ （φ0（t），φ1（t），…，φK（t）），0≤t≤T，表示投资在Sj（t），j＝0，1，…，K上的资产份数.如果φ（t）是Ft适应的（或Ht适应的），并且则称φ（t）是Ft可行策略（或Ht可行策略），Ft可行策略（或Ht可行策略）的集合记为AF（或AH）；如果存在着Ft可行策略φ（t）∈AF（或Ht可行策略φ（t）∈AH），使得

称欧式期权F为F可复制的（或H可复制的）；如果市场中的每个欧式期权F∈L2（θ）都是F可复制的（或H可复制的），则称此市场为F完全市场（或H完全市场）.

Lévy过程驱动的市场一般来说不是F完全市场（或H完全市场）.一方面，Lévy过程跳跃的高度是难以获知的；另一方面，资产组合的选择限制在S1（t），…，Sk（t）上，k≤K.当欧式期权不能用资产组合F完全复制（或H完全复制）时，投资者希望找到“最保险”的复制策略，即文献[14]提出的方差最小复制策略.

定义6 对于平方可积的欧式期权F∈L2（θ），若存在着φ（t）∈AH（或φ（t）∈AF）使

则称φ（t）为F的H（或F）方差最小复制策略.

3 方差最小复制策略及市场固有风险

本章用Malliavin导数表示欧式期权F的方差最小复制策略，主要理论依据是L2（θ）上的CHO定理.

定理2 在Lévy过程所驱动的市场式（5）、（6）中，欧式期权F∈L2（θ）的F方差最小复制策略ψ（t）＝ （ψ0（t），ψ1（t），…，ψk（t））表示为

证明 给定平方可积Lévy白噪声泛函F∈L2（θ），根据L2（θ）上的CHO定理，F具有如下分解：

其中Bj（t）为布朗运动是Lévy过程ηj（t）的正交幂跳过程.

令ψ（t）为F的F方差最小复制策略.因为所以由ψ（t）复制的价值为

由于L2（FT，π）是 Hilbert空间，根据方差最小复制策略的定义6，即找到φ＊（t），使得

对于任意的具有下列形式的Ξ∈L2（FT，θ）都成立，这里

其中εj∈AF.将式（9）、（10）和（12）代入式（11），可得

根据Y（m）（t）的正交性[16]，上式写为

由εj∈AF的任意性，根据式（14），可得式（8），定理得证.

由定理2和条件数学期望的性质，可直接得到部分信息的H方差最小复制策略.

推论1 在Lévy过程所驱动的市场式（5）、（6）中，欧式期权F∈L2（θ）的H方差最小复制策略为

在Lévy过程驱动的金融市场中，当投资者对F∈L2（θ）选择复制策略时，由于跳跃过程和资产选择的限制不能实现对欧式期权F完全复制.这是市场本身所存在的不可规避的风险，称之为市场固有风险.市场固有风险不包括信息缺失所带来的风险.

定理3 在Lévy过程驱动的金融市场式（5）、（6）中，系统的固有风险为

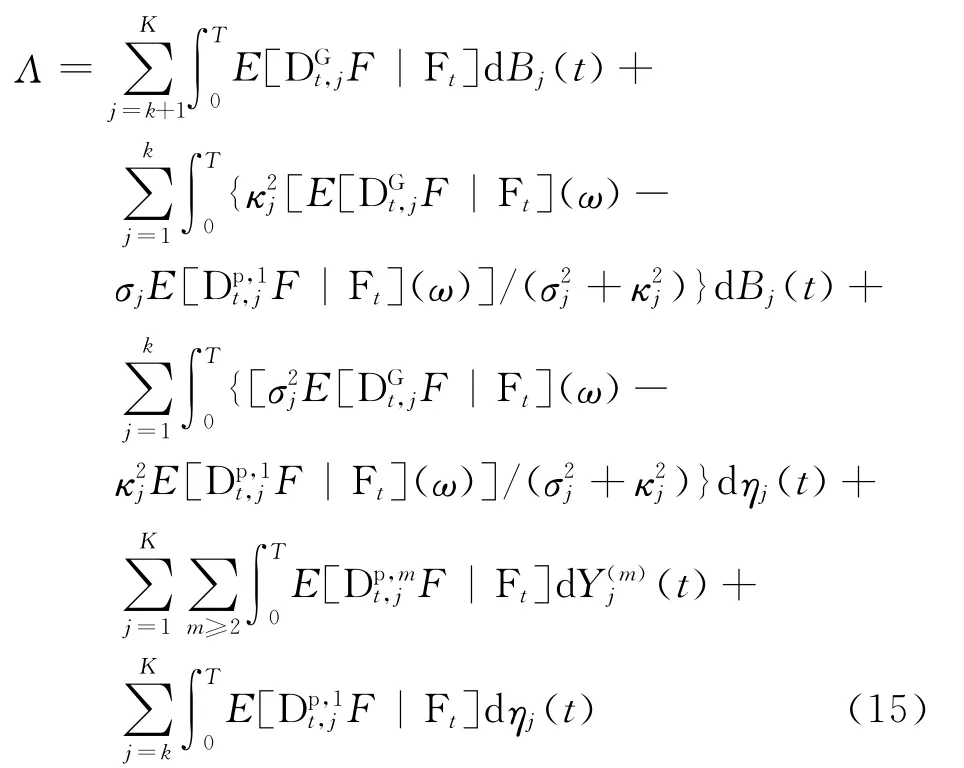
证明 给定平方可积Lévy白噪声泛函F∈L2（θ），根据L2（θ）上的CHO定理，F具有分解

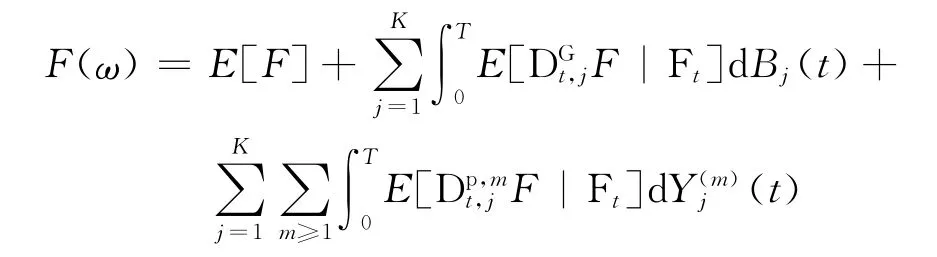
令表示F方差最小复制策略φ（t）＝ （φ0（t），φ1（t），…，φk（t）），0≤t≤T，k≤K所复制的价值，则

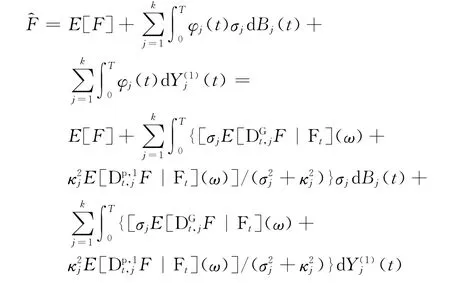
将F和代入固有风险Λ＝F－的定义，可得到式（15），证毕.

推论2 如果金融市场由补偿Poisson过程（t）驱动，即（t）＝（t），且k＝K，则有Λ＝0.

证明 当（t）＝（t）时，对给定平方可积Lévy白噪声泛函F∈L2（μp），根据L2（μp）上的CHO 定 理，F具 有 分 解F（ω） ＝E[F]＋令 表示F方差最小复制 策 略φ（t）＝ （φ0（t），φ1（t），…，φk（t）），0 ≤t≤T，k≤K所复制的价值，则

将F和代入固有风险Λ＝F－的定义，可得Λ＝0，那么Lévy过程驱动的金融市场是完全市场.

由此，当所有的K个风险资产都用来组成复制策略时，Lévy过程的特例（t）＝（t）所驱动的市场是完全的.□

4 结 语

本文研究由布朗运动和纯跳Lévy过程复合的Lévy过程驱动的金融市场.此市场既有连续波动的性质，又复合了如金融危机等重大金融事件所造成的不规则跳跃式波动.白噪声分析的方法应用于金融市场在文献[3]和[14]中都有所研究，文献[3]用Gauss白噪声分析研究布朗运动驱动的金融市场，而文献[14]用纯跳Lévy白噪声分析研究纯跳Lévy过程驱动的金融市场.本文的模型是文献[3]和[14]中模型的复合.在Gauss白噪声和纯跳Lévy白噪声复合的Lévy白噪声框架下，应用CHO定理，用Malliavin导数具体表示了欧式期权的方差最小复制策略和市场固有风险.因此，本文的结果包含了文献[3]和[14]的结果，而且更贴近现实中一般的金融市场.

[1] KARATZAS I，OCONE D.A generalized Clark representation formula，with application to optimal portfolios [J].Stochastics and Stochastic Reports，1991，34（2）：187－220

[2] HIDA Takeyuki. White noise analysis and its applications [J]. North－Holland Mathematical Studies，1982，74：43－48

[3] AASE K， KSENDAL B，PRIVAULT N，etal.White noise generalizations of Clark－Haussmann－Ocone theorem with application to mathematical finance [J].Finance and Stochastics，2000，4（4）：465－496

[4] ELLIOTT R，VAN DER HORK J.A general fractional white noise theory and applications to finance[J].Mathematical Finance，2003，13（2）：301－330

[5] HU Y， KSENDAL B.Fractional white noise calculus and applications to finance [J].Infinite Dimensional Analysis Quantum Probability Related Topics，2003，6（1）：1－32

[6] EBERLEIN E， KELLER U. Hyperbolic distributions in finance[J].Bernoulli，1995，1（3）：281－299

[7] BARNDORFF－NIELSEN E.Processes of normal inverse Gaussian type[J].Finance and Stochastics，1998，2（1）：41－68

[8] SCHOUTENS W.Lévy Processes in Finance[M].Hoboken：Wiley Blackwell，2003

[9] CONT R，TANKOV P.Financial Modeling with Jump Processes[M].London：Chapman ＆ Hall/CRC Press，2003

[10] APPLEBAUM D.Lévy Processes and Stochastic Calculus [M].Cambridge：Cambridge University Press，2004

[11] L KKA A， KSENDAL B， PROSKE F.Stochastic partial differential equations driven by Lévy space－time white noise [J].The Annals of Applied Probability，2004，14（3）：1506－1528

[12] 冯敬海，王 岩，冯恩民.由纯跳Lévy白噪声驱动的随机薛定谔方程[J].大连理工大学学报，2008，48（5）：769－774（FENG Jing－hai， WANG Yan，FENG En－min.Stochastic Schr dinger equation driven by pure jump Lévy white noise[J].Journal of Dalian University of Technology，2008，48（5）：769－774）

[13] L KKA A.Martingale representation of functionals of Lévy processes [J].Stochastic Analysis and Applications，2004，22：867－892

[14] DI NUNNO G， KSENDAL B，PROSKE F.White noise analysis for Lévy processes[J].Journal of Functional Analysis，2004，206（1）：109－148

[15] 冯敬海，王 岩，冯恩民.复合白噪声驱动的输运方程 [J].应用概率统计，2009，25（6）：597－610

[16] NUALART D，SCHOUTENS W.Chaotic and predictable representations for Lévy processes[J].Stochastic Processes and Their Applications，2000，90（1）：109－122