考虑土拱效应的高速铁路路堤基底压力的简化算法

刘俊飞，赵国堂，马建林

(1.中铁第五勘察设计院集团有限公司地路分院，北京 102600;2.西南交通大学土木工程学院，成都 610031;3.京沪高速铁路股份有限公司，北京 100038)

路堤填土自重和路堤上荷载通过路堤本身传递到地基表面，形成路堤与地基界面的接触压力，这个应力称为“基底压力”或“基底应力”。这部分压力也是地基所承受的荷载，即地基表面的附加应力。获知路堤的基底压力是进行地基沉降计算的前提。通常采用“法向荷载近似法［1］”进行路堤基底压力计算，即近似地取为容重γ乘以此处的路堤高度h。然而，实际上路堤填筑后会出现路堤中心处基底压力小于自重，路基两侧基底压力大于自重，即应力分布出现均匀化的现象。有学者把这种现象解释为由于地基盆状沉降，路堤或堤坝中部向下变形量大导致的土拱效应［2］。

基底压力分布的变化将会影响到地基中附加应力的分布和地基沉降变形计算结果的大小。对于以沉降控制为主的高速铁路路基，基底压力的准确计算就显得更为重要。

Perloff和Baladi等假设路堤和地基是连续的一个整体，只受到其自重作用，得到其平面应变条件下的弹性解析解［3］，称为“弹性土堤法”［1，4］。但是弹性土堤法的假定与实际情况存在一定的偏差，例如路堤填土和地基土均有一定的塑性性质，实际工程中路堤与地基的力学性质也常常有所差异，这将给其计算结果带来一定的偏差。另一方面，采用弹性土堤法计算较为复杂，不利于工程应用。

本文将通过使用PLAXIS岩土有限元程序对高速铁路路堤进行了不同填土摩擦角、填土高度和地基土模量情况下基底压力的数值模拟计算分析和反演计算，得出适用于高速铁路路堤的基底压力简化算法。

1 路堤物理模型

高速铁路路堤为满足轨道高平顺、高稳定的要求，通常对软弱地基进行CFG桩复合地基处理等措施，改善地基变形性质，同时采用加强的路基材料，改善了路基的变形性质。

根据《高速铁路设计规范》［5］，正线区间直线地段线间距为5 m时，采用无砟轨道的高速铁路路基面宽度双线为13.6 m，有砟轨道双线为13.8 m。路堤边坡坡度一般采用1∶1.5。路堤填土包含基床和基床以下路堤两个部分，基床分为基床表层和基床底层。基床表层厚度无砟轨道为0.4 m，有砟轨道路为0.7 m，基床底层厚度2.3 m。基床表层多采用级配碎石填筑，基床底层和基床以下路堤多采用A、B组填料填筑，并满足相应的填筑标准。

采用PLAXIS有限元程序模拟路基填筑。填土重度按20 kN/m3计算，压缩模量取60 MPa。

2 路堤下基底压力的有限元计算结果分析

路基填土后地基和路基的沉降变形和应力计算结果如图1所示。在路堤自重荷载作用下，地基沉降呈盆状，路堤中部沉降大，坡脚处沉降小。

图1 路堤填筑后产生的盆状沉降

路基填土后地基和路基的应力计算结果如图2所示。地基的不均匀沉降使土体之间出现相对位移，产生剪切力，在路堤两侧造成主应力方向偏离重力方向，路堤中心的一部分竖向应力向两侧转移而减小，同时路堤两侧竖向应力增大。这种在土体之间产生相对位移的条件下，土体调动自身的抗剪强度产生剪切力，使土压力从位移土体转移到邻近相对静止土体，即路堤中出现了“土拱效应”。路堤中的土拱效应在一定程度上均化了路堤中心与两侧竖向应力分布的差异和沉降差异。

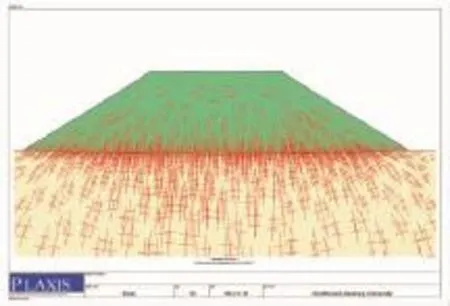
图2 填土中主应力大小和方向

路堤填土高度和地基土的变形性质的变化将改变地基盆状沉降的形态，填土抗剪强度的不同也会导致土体间的剪切力的不同，这些因素都将影响路堤中土拱效应的发挥。下面就对路堤填土摩擦角、填土高度和地基土模量对基底压力的影响进行计算分析。

2.1 路堤填土摩擦角对基底压力的影响

路堤填土高10 m，其他条件相同，填土摩擦角分别为20°、30°、40°时路堤下基底压力分布的计算结果如图3所示。

图3 不同填土摩擦角时路堤下基底压力分布

可以看出，这些不同摩擦角的填土都出现了竖向应力向路堤两侧扩散的现象。在路堤中部，与路堤几何断面的顶面平台相对应，基底压力曲线也有一段相对均匀的“平台”，基底压力分布曲线基本形状仍以路堤断面为基础，大致保持梯形。路堤中部的基底压力随着填土摩擦角的增大而减小，填土摩擦角由20°增加到40°时，基底压力由填土自重的0.88倍降低到其0.78 倍。

2.2 路堤填高对基底压力的影响

填土摩擦角为40°，其他条件相同，不同路堤填高时路堤下基底压力分布见图4。

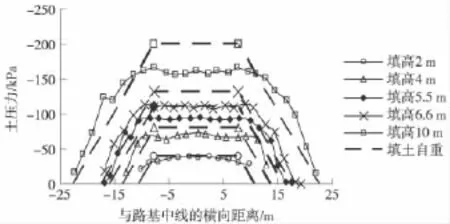
图4 不同填高时路堤下基底压力分布

可以看出，填高较小时路堤中部基底压力与填土自重较为接近，当填土高度为2 m时，路堤中部的基底压力为填土自重的0.96倍。随着填高的增大基底压力与填土自重之间的差值越来越大，基底压力与填土自重的比值随之减小。当填土高度增至10 m时，路堤中部的基底压力为填土自重的0.78倍。

2.3 地基土压缩模量对基底压力的影响

不同地基土压缩模量条件下的基底压力计算结果如图5所示。

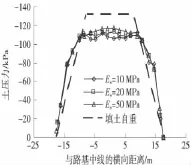
图5 不同地基土压缩模量时路堤基底压力分布

计算表明，随着地基土压缩模量的增大，路堤中部基底压力稍有增大。显示出随着地基沉降差异的减小，土拱效应有所减弱。另一方面，随着地基土模量的增加，基底压力增加的速度逐渐减小。总体上，地基土压缩模量Es由20 MPa增大到50 MPa时，路堤中部基底压力增大的幅度很小。

通过以上PLAXIS数值模拟分析可以认为:

(1)由于路堤中的土拱效应，路堤下基底压力出现由路堤中部向两侧扩散的现象。在路堤中部，与路堤几何断面的顶面平台相对应，扩散后的基底压力曲线也有一段相对均匀的“平台”，基底压力分布曲线基本形状仍以路堤断面为基础，大致保持梯形;

(2)路堤中部的基底压力与填土自重之比随着填土摩擦角的增大而减小，随着填高的增大而增大;

(3)随着地基土压缩模量增大，路堤中部的基底压力与填土自重之比有所增加，但在常见地基土或复合地基压缩模量范围内，总体上变化范围不大。

3 路堤下基底压力的简化算法——扩散角法

通过前面的分析可知，路堤中的土拱效应将导致路堤中部基底压力向两侧“转移”，这种现象类似于土体中常见的应力扩散现象。因此本节将采用应力扩散的方法建立模型，对这一现象进行定量计算。

PLAXIS数值模拟结果显示出，路堤自重作用下基底压力在路堤中部出现有压力相对稳定的平台，基底压力分布曲线大致呈梯形，与路堤基本形状保持一致。因此可以按从路肩开始向下扩散的方法，采用扩散角θ来考虑路堤下基底压力“扩散”，扩散后的基底压力分布曲线仍按梯形简化(图6)。

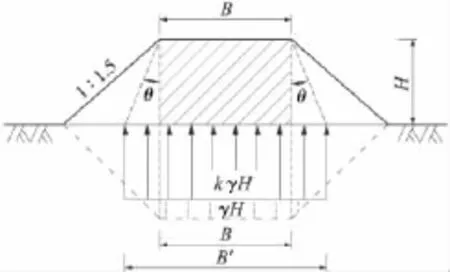
图6 扩散角示意

如图6所示，路堤顶面平台宽度B范围内的土柱按自重压力计算时基底压力为γH，按照θ角扩散后，这些压力分布到宽度为B'=B+2H·tanθ的范围内，基底压力变为

式中，k为路堤中部基底压力折减系数。

θ角的确定采用根据PLAXIS模型计算结果进行反算的方法。根据图3中列出的PLAXIS模型计算结果，对不同填土摩擦角时的路堤中部基底压力进行反算(图7)得到扩散角约为填土摩擦角的1/3，即可取θ=φ/3。代入式(1)可得路堤中部基底压力折减系数

式中，φ为路堤填土摩擦角。

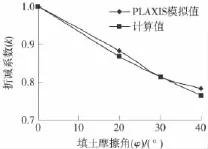
图7 不同填土摩擦角时路堤中部基底压力折减系数反算

然而，此时若取B'=B+2H·tan(φ/3)作为梯形基底压力分布图的底边宽度，则基底压力的合力将小于路堤自重压力，无法满足地基反力与路堤自重之间的平衡条件。这是路堤两侧的2个三角形土柱产生的基底压力并不符合线性简化所致。这也可以从图3～图5中得到体现:即路堤两侧的基底压力曲线略呈上凸状，取其弦线进行线性简化后将会使基底压力略有减小。

为了使扩散角法模型的梯形简化计算仍满足地基反力与路堤自重间的平衡条件，将梯形基底压力分布图的底边宽度由B'扩展到B1，并有

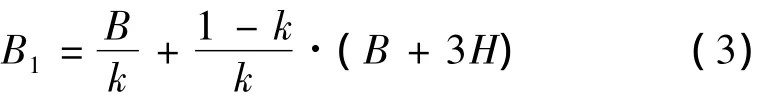
即，扩散角法计算路堤自重作用下基底压力的计算简图如图8所示。

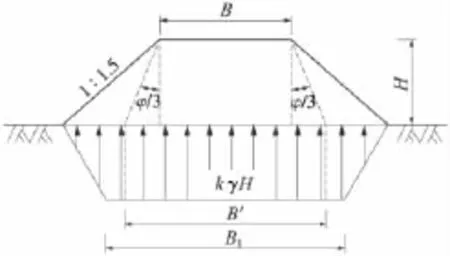
图8 路堤自重作用下地基反力计算简图

当路堤顶面承受宽度为b，大小为q0的均布荷载时，q0作用下地基压力计算简图如图9所示。扩散角仍取θ=φ/3，扩散至地基表面时作用宽度变为b1

q0作用下地基压力折减系数

图9 路堤顶部有均布荷载时路堤下地基反力计算简图

为了检验式(2)的可靠性，采用该式对图4所列出的5个模型模拟结果进行对比，可见，计算值与数值模拟结果吻合(图10)。

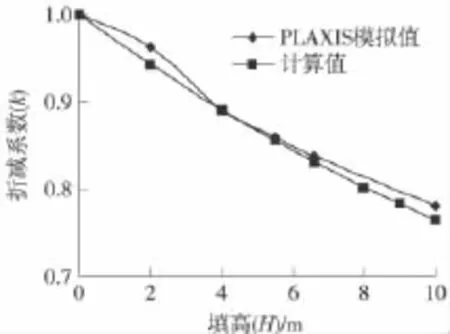
图10 不同填高时路堤中部基底压力折减系数计算对比

4 现场实测结果与计算值的对比

某高速铁路路堤填高约7 m，堆载预压3.5 m，地基采用CFG桩复合地基，桩顶设0.15 m厚碎石垫层，其上设0.5 m厚钢筋混凝土板。路堤A、B组填料填筑后实测湿容重约24 kN/m3。该段路堤中的2个断面从路基填筑起至填筑完成半年后，混凝土板上土压力测试结果见图11、图12。图中，对堆载预压土产生的荷载按照路堤顶面的均布荷载考虑。

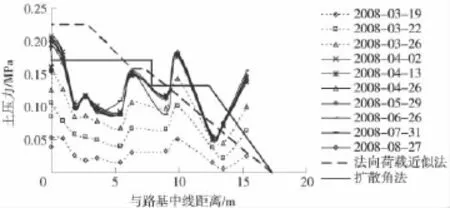
图11 断面1地基压力测试值与计算值对比

图12 断面2地基压力测试值与计算值对比

以上各断面连接各测点形成的土压力分布曲线有明显起伏，但对每个测点而言，数据就表现得较为稳定，这说明土压力盒工作状态正常。土压力分布曲线波动的原因是:这些土压力盒埋设于碎石类A、B组填料中，填料最大粒径一般控制在5 cm。而土压力盒直径仅约10 cm，高度也仅3 cm。土压力盒下表面为刚性混凝土板，而四周的碎石容易相互咬合，限制颗粒间的错动，导致土压力盒感应面受力不足，或应力集中导致感应面受力偏大，这就很容易引起压力盒测试值的不均匀，因此造成测试所得土压力分布曲线的起伏。需要说明的是，土压力盒测试值的不均匀并不能说明实际的桩顶平面土压力也不均匀。可以认为，虽然实测土压力曲线有所波动，但总体上仍能反映出地基压力的大小和变化趋势。

通过测试值与扩散角法计算值之间对比，可以判断:采用法向荷载近似法计算地基压力，会造成路基中部计算值偏大。采用扩散角法进行高速铁路路堤下地基压力计算更加符合实际。

文献［4］中列举了5 个工点［6～9］现场实测资料与法向荷载近似法、弹性土堤法等方法计算值结果的对比。这里增加扩散角法计算值与它们的对比，见表1。

表1 基底压力计算值与实测值的对比

对比结果可以看出，扩散角法对于列举的几个工点基底压力计算也是适用的。

5 结论

在路堤下基底压力数值模拟计算的基础上，建立了适用于高速铁路的路堤下基底压力的扩散角法计算模型。通过数值模拟以及计算值与现场实测值的对比与分析，有以下结论。

(1)由于路堤中的土拱效应，路堤下基底压力出现由路堤中部向两侧扩散的现象。在路堤中部，与路堤几何断面的顶面平台相对应，扩散后的基底压力曲线也有一段相对均匀的“平台”，基底压力分布曲线基本形状仍以路堤断面为基础，大致保持梯形。

(2)路堤中部的基底压力与填土自重之比随着填土摩擦角的增大而减小，随着填高的增大而增大。

(3)采用扩散角法计算路堤基底压力时，扩散角可取为填土摩擦角的1/3。采用扩散角法计算路堤基底压力，可以取得符合实际的计算结果。

［1］温特科恩，方晓阳.基础工程手册［M］.钱鸿缙，叶书麟译.北京:中国建筑工业出版社，1983.

［2］杨雪强，何世秀，庄心善.土木工程中的土拱效应［J］.湖北工学院学报，1994，9(1):1-7.

［3］W.H.Perloff，G.Y.Baladi，M.E.Harr.Stress distribution within and under long elastic embankments［J］.Highway Research Record，1967，181:12-40.

［4］蒋关鲁，王海龙，李安洪.高速铁路路基基底应力计算方法研究［J］.铁道建筑，2009(4).

［5］中华人民共和国铁道部.高速铁路设计规范(试行)［S］.北京:中国铁道出版社，2010.

［6］肖宏.高速铁路无砟轨道桩网结构路基研究［D］.成都:西南交通大学，2007.

［7］陈亚美.路基荷载下水泥搅拌桩复合地基现场测试与FEM分析［D］.成都:西南交通大学，2008.

［8］秦立新.加筋垫层桩承式路堤试验分析及机理研究［D］.武汉:武汉大学，2008.

［9］宋修广，陆洪健，于洪泽.粉喷桩加固高速公路路基的现场试验研究［J］.大坝观测与土工测试，2001，25(3):38-40.