椭圆型弹性球铰链转动性能及疲劳强度研究

李成刚 尤晶晶 吴洪涛

南京航空航天大学，南京，210016

0 引言

在微小型设备中，对实现小范围内偏转的支承，不仅要求分辨率高，而且要求尺寸微型化。弹性铰链符合上述要求，其中部较为薄弱，在弯矩的作用下可以产生弹性角变形，弯矩去除后又能恢复到原形。与传统铰链相比，弹性铰链具有体积小、无机械摩擦、无间隙、无回退空程等优点［1］。1965年，Paros等［2］首次给出了圆弧形弹性铰链的简化计算公式。基于不同的运动精度和运动范围，目前国内外研究的弹性铰链几何转角结构除圆弧形外还有直梁形［3］、椭圆形［4］、抛物线形［5］、双曲线形［6］等。

目前，弹性铰链的研究方法普遍采用数值积分法和有限元方法，研究对象主要集中在单轴和双轴转动［7－8］。由于横截面惯性矩、极惯性矩等几何量的不同，单轴或双轴弹性铰链的理论推导结论对三轴弹性铰链一般不适用；而球铰链在科学研究以及工业生产中被使用的频率相当高。本文系统地对椭圆形弹性球铰链的柔度、精度以及疲劳强度进行理论推导和分析，旨在为弹性球铰链材料的选择以及结构参数的优化设计等提供理论依据。

1 柔度计算

柔度是评价弹性铰链最重要的性能参数之一，在保证强度的前提下，通常希望铰链具有大的柔度以确保较少的能量损耗。椭圆形弹性球铰链的模型如图1所示，其任一轴切面如图2所示。其中，a、b分别为椭圆的长短半轴长；e为弹性铰链中柔性部分长度的一半；t为弹性铰链中厚度的最小值；θm为铰链中椭圆广角的一半；O点、B点所在的横截面分别是铰链柔性部分的起始面和终止面，将它们分别看作为固定端和自由端；球铰链的转动中心A点所在的横截面是铰链上柔性部分的最薄处。

图1 椭圆形弹性球铰链

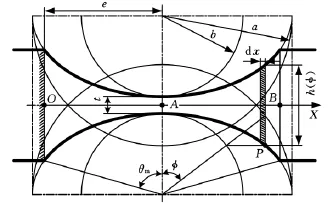
图2 椭圆形弹性球铰链轴切面

设铰链的轴线为X轴，原点选在O点。过铰链上任意点P的横截面的直径h（φ）以及面积A（φ）、惯性矩I（φ）、极惯性矩IP（φ）可以分别表示为

在弹性球铰链的自由端作用弯矩M时，铰链会发生弯曲变形，表现为横截面绕其中性轴转动；作用扭矩T时，铰链会发生扭转变形，表现为各横截面之间绕铰链轴线相对转动了一个角度。为了定量地考察弹性球铰链的柔度特性，定义A、B两个横截面在单位弯矩下的转角差θAB表征弯曲柔度，截面B在单位扭矩下的转角φB表征扭转柔度。

应用卡氏第二定理，可以分别计算在弯矩M的作用下A、B截面绕其中性轴转动的角位移θA和θB：

式中，E为铰链材料的弹性模量；MA为在A截面虚加的弯矩。

根据定义，计算弹性球铰链的弯曲柔度：

应用卡氏第二定理，求解在扭矩T作用下截面B相对于固定端的扭转角：

式中，G为铰链材料的切变模量。

计算弹性球铰链的扭转柔度：

2 精度计算

由于弹性铰链是通过弹性变形来实现铰链运动的，施加在铰链上的广义力会导致铰链中心点偏离其几何中心，进而影响弹性铰链的精度。当在铰链的自由端作用弯矩M时，中心点A会产生一个挠度ωA，定义单位弯矩下的挠度为弯曲精度；当在铰链的自由端作用拉力F时，中心点A会偏移一段距离ΔA，定义单位拉力下的偏移为拉伸精度。

应用卡氏第二定理，计算在弯矩M作用下A点挠度：

计算弹性球铰链的弯曲精度：

在拉力F作用下，计算A点偏移量：

3 柔度精度比

由式（7）、式（9）、式（11）、式（13）可以看出：弹性球铰链的柔度和精度往往是矛盾的，很难同时保证两个指标都高。例如，椭圆的长短半轴之比越大，则铰链的柔度越大，但精度会越低。为了兼顾柔度和精度，本文提出一个全新的概念：将弹性球铰链的柔度精度比作为评价弹性球铰链性能的综合指标，并记作V。定义

显然，V值越大，表征弹性球铰链的综合性能越好。将式（7）、式（9）、式（11）、式（13）代入式（14），得到弹性球铰链柔度精度比的解析表达式：

借助于Mat hematica软件强大的符号运算以及绘图功能，绘制二元函数J（ε，θm）的曲面图，如图3所示，其中，ε、J（ε，θm）均是量纲一参量。

在保证强度的前提下，根据式（15）和图3可以分析得到，椭圆形弹性球铰链的材料特性以及结构参数与其综合性能满足如下关系：

（1）材料的弹性模量越大、切变模量越小，则弹性球铰链的综合性能越好。

（2）椭圆长短半轴之比越小，则铰链的综合性能越好，即圆弧形弹性球铰链的综合性能比椭圆形的综合性能好。

（3）铰链最小厚度与椭圆短半轴之比越大，则其综合性能越差；但当此比例大于0．8时，最小厚度对球铰链性能的影响不再明显。

（4）铰链的广角越大，则其综合性能越差；但当广角大于2．5rad（即θm＞1．25rad）时，其对球铰链性能的影响不再明显。

（5）弹性球铰链的几何尺寸越小，则其综合性能越好。

图3 二元函数J（ε，θm）的曲面图

4 疲劳强度校验

上文通过理论推导，在满足强度的前提下，得到了关于椭圆形弹性球铰链优化设计的5个结论。然而，弹性球铰链通常工作于交变应力环境下，为了使其不发生疲劳破坏，有必要推导出铰链疲劳强度的校验公式。显然，铰链的危险截面是厚度最小的横截面A。在自由端同时作用弯矩M、拉力F和扭矩T时，危险截面上距离中性轴最远处的应力值最大，其最大正应力σmax和最大切应力τmax分别为

根据第三强度理论以及疲劳强度的经验公式［9］，可以推导出在同步的拉弯扭组合对称循环交变应力作用下弹性球铰的疲劳强度校验公式：

式中，nστ、nσ、nτ分别为弹 性 铰 链在组合 交 变 应力、正应力、切应力下的工作安全系数；n为人为规定的弹性铰链工作安全系数；σ－1、τ－1分别为正应力和切应力的疲劳极限；kσ、kτ分别为应力集中对正应力和切应力的影响系数；εσ、ετ分别为弹性铰链的几何尺寸对正应力和切应力的影响系数，β为材料表面加工的影响系数。

由式（16）～式（18），可以计算得到弹性球铰链疲劳强度的校验公式：

施加在弹性球铰链自由端的广义力、铰链的材料特性、最小厚度以及加工工艺等满足不等式（19）时，铰链才能够经受至少107次交变载荷的作用而不产生断裂现象。可见，在设计弹性球铰链时不能只是一味地追求柔度、精度等性能，而不考虑其疲劳强度。

5 应用实例

为了使弹性球铰链具有良好的转动性能，依据第3节最后所得到的第一个结论，设计时应选用弹性模量大而切变模量小的材料。在产品的设计阶段，除了材料的选择之外，设计人员还面临一个合理确定各尺寸参数的难题。例如，在设计椭圆形弹性球铰链时，有几组尺寸参数可供选择，表1列出了其中的4组选择方案。

表1 椭圆形弹性球铰链尺寸参数的选择方案

依据第3节最后所得到的后4个结论，可以对表1中的4组方案做出优劣判断，其中，方案4的弹性球铰链的转动性能最优。确定尺寸参数之后，再根据铰链的材料特性、表面加工处理工艺、作用在铰链上的载荷以及不等式（19）对弹性球铰链的疲劳强度进行校验。如果不等式成立，则该方案满足设计要求；否则，应增大最小厚度t，直到不等式（19）成立为止。这样，设计出来的椭圆形弹性球铰链一定是最优的。

6 结束语

本文系统地研究了椭圆形弹性球铰链的转动能力和转动精度，以力学卡氏第二定理为理论基础，通过引入中间变量，并将椭圆的离心角作为积分变量，推导出弹性球铰链弯曲柔度、扭转柔度、弯曲精度以及拉伸精度的解析表达式。提出弹性球铰链柔度精度比的概念，给出了其定义表达式，并以此作为评价弹性铰链综合性能的指标；通过计算得到了在满足强度的前提下提高该指标的措施，即铰链应选用弹性模量大、切变模量小的材料；椭圆广角、椭圆长短半轴之比以及铰链最小厚度与椭圆短半轴之比都应尽可能小。推导了弹性球铰链疲劳强度的校验公式，用于检验设计出的铰链能否满足工作需求。最后，通过一个应用实例介绍了弹性球铰链的详细设计过程。

［1］ Yeh H C，Ni W T，Pan S S．Digital Closed－loop Nanopositioning Using Rectilinear Flexure Stage and Laser Interfer o metry［J］．Contr ol Engineering Practice，2005，13：559－566．

［2］ Paros J M，Weisboro L．How to Design Flexure Hinges［J］．Machine Design，1965，37：151－157．

［3］ 秦宇，冯之敬．直梁型柔性铰链制造误差对刚度性能影响的建模与分析［J］．中国机械工程，2008，19（18）：2182－2185．

［4］ 陈贵敏，韩琪．深切口椭圆柔性铰链［J］．光学精密工程，2009，17（3）：570－575．

［5］ Nicolae L，Jeffrey S N，Ed ward O M，et al．Parabolic and Hyper bolic Flexure Hinges：Flexibility，Motion Precision and Stress Characterization Based on Co mpliance Closed－for m Equations［J］．Precision Engineering，2002，26：183－192．

［6］ Nicolae L，Jeffrey S N，Ephrahim G．Design of Sy mmetric Conic－section Flexure Hinges Based on Closed－for m Compliance Equations［J］．Mechanism and Machine Theory，2002，37：477－498．

［7］ 吴鹰飞，周兆英．柔性铰链转动刚度计算公式的推导［J］．仪器仪表学报，2004，25（1）：125－128．

［8］ Awtar S，Slocu m A H，Sevincer E．Characteristics of Beam－based Flexure Modules［J］．ASME Journal of Mechanical Design，2007，129（6）：625－639．

［9］ 戴少度．材料力学［M］．北京：国防工业出版社，2000．