基于应力场强法的随机载荷作用下转向节疲劳寿命预估

黄海波 陈星欣 翁胜峰

宁波大学,宁波,315211

0 引言

随着汽车工业的发展,在轻量化设计的同时,对汽车的安全性和可靠性要求越来越高,这就需要一种快速有效的系统级零部件疲劳分析设计方法来缩短产品的设计周期,进而降低开发成本,提高市场竞争力。传统的试验场道路耐久性试验和室内台架试验耗时长,成本高[1-2],同时在概念设计阶段也无法进行实物的耐久性物理试验。传统的疲劳耐久有限元分析的应力应变时间历程是基于线弹性的材料模型来获得的,这与实际的材料特性不符合,导致疲劳寿命误差较大[3]。疲劳寿命的评估精度除了依赖于材料疲劳性能数据、疲劳损伤模型外,还依赖于试件在真实路况下的随机载荷谱和准确的应力应变响应。

转向节是汽车悬架的重要部件之一,承受转向轮的负载以及路面传递来的冲击,同时还承受来自转向器的转向力,实现转向功能,对其强度、抗冲击性以及可靠性方面都有很高的要求。本文结合多体系统动力学、有限元方法以及疲劳损伤计算中的应力场强法理论,充分考虑各个系统部件的非线性特性、边界条件和实际的材料特性,计算了某商用车双横臂悬架转向节的疲劳寿命,为汽车部件的疲劳寿命预测及改进提供了方法和借鉴。

图1 悬架系统各部件及约束位置

1 悬架系统建模

1.1 悬架系统虚拟样机建模

本文研究对象为双横臂扭杆弹簧式悬架系统,如图1所示。利用三维造型软件建立数字模型并导入多体动力学软件中。在建模过程中考虑了减振器、扭杆弹簧以及非对称衬套的非线性影响和预载,各个部件之间的约束关系见表1。整个模型共有5个自由度,除去激励板和轮胎附着板的两个垂向自由度,前悬架共有3个自由度,分别为前轮的垂向运动、绕主销轴线的前后摆动以及垂直面内的内外摆动,与实际情况相符。非线性衬套、弹簧和减振器的非线性建模及预载施加参见文献[4]。

表1 前悬架动力学模型约束说明

由于需要计算转向节的疲劳寿命,因此必须将转向节柔性化,用模态矢量和模态坐标的线性组合来表示转向节的弹性位移,计算每一时刻物体的应力应变。转向节的材料为各向同性弹塑性金属材料 40CR-GB/T3077,密度为 7820 kg/m3,泊松比为0.28,弹性模量为 208GPa。本文中用到的转向节共有3个铰接孔和1个连接轴头,分别为上下横臂铰接孔、转向拉杆铰接孔以及用于连接轮毂的轴头。为保证柔性化的准确性,在连接中心处建立节点并利用Mass 21单元(类似哑物体,无质量,刚度无限大)进行网格划分,对其周围的孔点进行耦合,建立以节点为中心的刚性区域。为了提高数据的计算效率,去除转向节低阶(＜10-3Hz)和高阶(＞104Hz)模态频率,完成后的柔性体如图2所示。

图2 转向节柔性体及其刚性区域

同时,本课题组还对双横臂悬架系统进行了模态分析试验来验证虚拟样机模型的准确性。实验系统如图3所示,采用激振器进行激励,单点激励多点响应,测试悬架系统的模态特性,试验结果与仿真结果有较好的一致性[5],系统的模态频率误差不超过10%,相似频率下的振型一致,验证了虚拟样机的准确性。

1.2 随机激励获取

悬架系统模型以国家B级路面谱[6]为激励,速度为70km/h,该激励是一个随机载荷谱,如图4所示。在这种情况下,转向节在3个铰接孔和1个连接轴头处都会存在包括弯、扭、拉、压等在内的实时应力应变。在多体动力学软件中设置时间步长为0.005s,时间为6s,仿真后截取转向节在3个铰接点和1个固定点处其中的铰接处5的六分力时域曲线,结果如图5所示。利用软件之间的接口,即可将数据流组导入有限元软件中进行应力应变计算。

图3 悬架系统试验

图4 国家B级路面谱

图5 铰接处5的六分力时域曲线

在计算转向节的时间—应力应变历程中,经过统计得到95%的最大应力点出现在连接车轮的横臂附近,因此笔者认为连接车轮的横臂处最易发生疲劳破坏。图6给出了连接车轮处横臂节点的等效应力云图。

由于转向节在受到路面随机激励时,一般发生弹性变形,塑性变形很少,随着循环次数的增加,屈服面移动,具有运动硬化特性,因此在有限元计算过程中,弹塑性材料特性采用多线性运动硬化模型,屈服准则宜采用von Mises准则[7]。本文将采取应力场强法进行疲劳损伤寿命预测,其技术路线如图7所示。

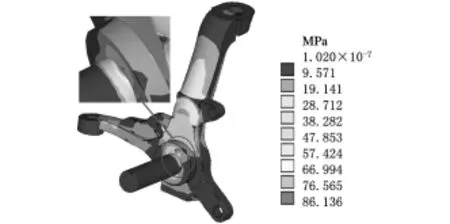
图6 连接车轮横臂处的节点等效应力

图7 疲劳损伤寿命预测方法技术路线

3 转向节疲劳损伤计算

3.1 应力场强法

目前,预测金属材料疲劳寿命的方法主要有名义应力法、局部应力应变法、损伤容限法以及能量法等。名义应力法以名义应力和应力集中系数为控制参数,以S-N曲线为主要依据,能够较好地预测低应力水平的疲劳寿命[8];局部应力应变法以局部危险部位的应力和应变为控制参数,在较高应力水平时预测结果较好[9];损伤容限法用断裂力学关于疲劳裂纹扩展的理论和方法来确定结构存在缺陷或裂纹,主要用于航天航空领域[10];能量法认为塑性功的累积是产生材料不可逆损伤进而导致疲劳破坏的主要原因,将有效损伤能耗作为损伤依据,建立起循环能耗-寿命曲线进行寿命预测。但其本构关系难以得到,工程应用上存在困难[11]。而应力场强法[12]利用应力场强作为疲劳控制参数,突破了点应力准则的限制,能较好地考虑疲劳根部破坏区域内的最大应力、应力梯度和应力状态对缺口强度的影响,符合材料的破坏机理[11],而估算结构疲劳寿命所需要的材料疲劳性能数据与名义应力法或局部应力应变法相同,分析过程也较为类似。因此本文基于应力场强法来计算转向节的疲劳寿命。

应力场强法从场的观点出发研究材料疲劳,基于材料的循环应力应变曲线,通过弹塑性有限元分析计算部件的应力场强度历程作为疲劳控制参数,然后根据材料的p-S-N曲线,结合疲劳累积损伤理论,估算部件的疲劳寿命。利用场强法计算疲劳损伤的思想是基于“外力”作用使材料微观结构产生不可逆的变化。应力场强法估算结构疲劳寿命所需要的材料疲劳性能数据与名义应力法或局部应力应变法相同,分析过程也较为类似,但其能够考虑破坏区周围应力、应变对某一疲劳损伤区域的作用,能较好地解释某些名义应力法和局部应力应变法无法解释的疲劳现象。应力场强法的公式为

式中,σFI为应力场强度;Ω为缺口破坏区;V为Ω的体积;f(σij)为破坏应力函数;φ(r)为权函数。

疲劳裂纹的萌生都与萌生处数个晶粒至数十个晶粒内疲劳损伤的累积有关,Ω的大小和形状与疲劳破坏机理有关,Ω一般为数个晶粒的尺寸。从宏观力学的角度,可以认为破坏区是以缺口根部为圆心的一个圆或椭圆,场径r是衡量局部破坏区域Ω大小的参数,目前主要通过试验和p-S-N曲线确定某种材料的场径,r越大,σFI越小。这里,由于在计算时得到的转向节应力较其屈服应力小(低应力),因此本文引用文献[13]研究成果中的低应力场径值,取r=0.56mm。

破坏应力函数f(σij)反映了材料和应力场两个因素对缺口强度的影响,函数 f(σij)的具体形式涉及材料的破坏机理,它主要解决以下问题：什么因素导致处于均匀应力应变场的光滑试件出现疲劳损伤并逐步累积以至疲劳破坏。材料不同,适用的强度理论也有所不同。对于疲劳破坏,情况也有类似。不同的材料其 f(σij)不同,在比例加载下,对于碳钢、铝合金、钛合金等宏观各向同性韧性金属材料,f(σij)可用von Mises等效应力公式计算[12],即

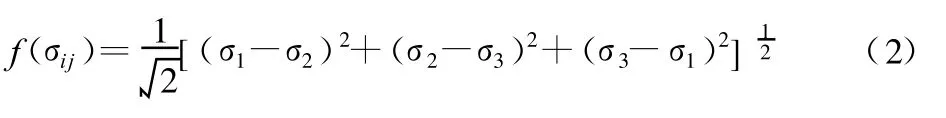
权函数φ(r)为在物理上表征 Ω内的任意一点处应力对|r|处峰值应力的贡献。从疲劳破坏的机理看,材料的疲劳损伤累积不是在缺口根部一“点”处进行的,因此疲劳损伤的累积不仅与缺口根部的最大应力应变有关,而且还与某一范围内的应力应变场有关。因此对于各项同性材料,φ(r)与缺口几何形状有关,0≤φ(r)≤1。一般而言,缺口根部的应力集中最严重,对疲劳裂纹的贡献最大,取 φ(0)=1。这里,考虑距离因素忽略方向的影响,取应力梯度G来计算权函数φ(r),梯度的选择取决于最大应力点周围是否较大范围地进入了塑性流动状态,具体公式为[8]

其中低应力水平时G取应力梯度,高应力水平时G取应变梯度。这里经过计算,转向节的应力在低应力水平,因此G取应力梯度,计算公式为

式中,σei为单元等效应力;σmax为破坏区内的最大等效应力。

由于单元等效应力σei在非静载下是变化的,因此权函数是实时变化的。

按场强计算公式(式(1)),缺口试件的破坏准则为

式中,σf为材料的疲劳极限。

即当缺口试件的场强σFI历程大于等于同种材料的疲劳极限σf时,缺口试件达到疲劳极限。

3.2 转向节材料的p-S-N曲线

p-S-N是疲劳计算中非常关键的参数[12],它是不同成活率p下的S-N曲线集。p-S-N曲线在有限寿命阶段在双对数坐标系上近似为一条直线：

式中,Np为存活率为p时的疲劳寿命;S为应力,它对应于某一应力比的应力幅值Sa或最大应力值Smax;ap和bp为与存活率有关的材料常数。

根据汽车零部件的设计要求,转向节为汽车的重要零部件,本文取存活率p=90%,即在此应力水平下零部件发生疲劳破坏的概率为10%。查表得转向节材料40CR-GB/T3077的材料参数：ap=23.7437,bp=-6.8610。

3.3 线性疲劳累积损伤理论

线性疲劳累积损伤理论[12]是指在循环载荷作用下,疲劳损伤可以线性地累加,各个应力之间相互独立,当累加的损伤达到某一个值时,试件发生疲劳破坏。线性累积损伤理论中比较常用的是Palmgren-Miner理论 ,简称 Miner理论。Miner理论认为,在变幅载荷下,n个循环造成的损伤为

式中,Ni为对应于当前载荷水平Si的疲劳寿命。

Miner理论是一个线性疲劳载荷次序的影响,而实际上加载次序对疲劳寿命的影响很大,对此已有了大量的实验研究。本文中转向节受到的为随机载荷谱,其临界损伤值DCR在1附近,这正是本文使用Miner理论的主要原因[14]。

3.4 转向节疲劳寿命的计算

本文中转向节受到的激励为国家B级路面谱,是一随机过程,采用单参数法只能记录应力的幅值量程,而没有记录幅值的绝对值。使用雨流计数法可以弥补单参数计数法的缺点,保证计数结果安全。因此通过数值分析软件利用公式(式(1))编程计算得到连接轮胎横臂处的场强时间历程,截取6s时历程曲线,如图8所示。在MATLAB中调用雨流统计法工具,即可求得易疲劳损伤点的场强幅值。

图8 场强 —时间历程

利用式(5),根据雨流计数结果,可以求得各幅值下的疲劳寿命N′,然后求得该幅值下的疲劳损伤D=n/N′,结果如表1所示。

表1 转向节的疲劳损伤

根据表1和式(6)可以得到对应场强幅值的应力损伤,求得在一个循环内转向节连接车轮横臂处的疲劳累积损伤为

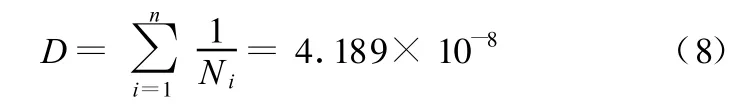
因此,其疲劳寿命为

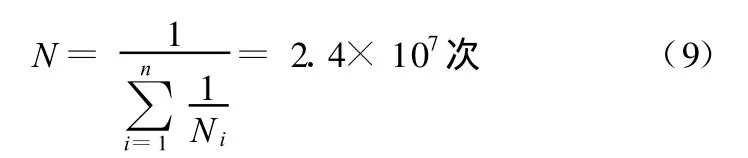
4 结论

(1)建立了经过实验验证的精确悬架系统动力学模型,利用国家B级路面谱进行激励,得到了转向节各铰接处的随机载荷谱,使激励和分析载荷更接近于真实情况,结果的真实性和可靠性更高。

(2)得到了转向节的应力应变集中点,其位置在连接车轮的横臂处,此处也是最早容易发生疲劳损伤的位置,并预估了转向节在B级路面下的疲劳寿命。

(3)基于应力场强法,考虑材料和应力场之间的相互影响、破坏区的范围以及各处应力对峰值应力的影响,利用雨流计数法统计场强应力分布,计算得到不同场强下的疲劳累积损伤,为各种部件的寿命计算提供了一种可供借鉴的方法。由于应力场强法在计算场强应力时考虑了周围点应力的影响,因此与实际情况更接近,其疲劳循环寿命为2.4×107次。

[1] 郭虎,陈文华,樊晓燕,等.汽车试验场可靠性试验强化系数的研究[J].机械工程学报,2004,40(10)：73-76.

[2] 王霄锋,管迪华,何泽民.汽车零部件室内耐久性试验方法研究[J].汽车工程,1992,4：224.

[3] Heyes P,Dakin J,Christopher S J.The Assessment and Useof Linear Static FE Stress Analyses for Durability Calculations[C]//International Conference on Vehicle Structure Mechanics&Cae.Troy：SAE,1995：951101.

[4] 黄海波,俞国强,贺华波,等.车辆底盘关键零部件性能对轮胎异常磨损影响的研究[R].宁波：宁波大学,2010.

[5] 黄兴,段小成.江淮1/4前悬架系统实验模态报告,TPR0911601[R].宁波：宁波拓普减震系统有限公司,2010.

[6] 于至生.汽车理论[M].3版.北京：机械工业出版社,2000.

[7] 姚卫星.金属材料疲劳行为的应力场法描述[J].固体力学学报,1997,18(1)：38-48.

[8] 袁熙,李舜酩.疲劳寿命预测方法的研究现状与发展[J].航空制造技术,2005(12)：80-84.

[9] 周炜,周宏,冯展辉.应用局部应力应变法估算机械疲劳寿命[J].同济大学学报,2001,29(8)：928-931.[10] 翟新康.飞机整体翼梁结构损伤容限试验及分析研究[D].西安：西北工业大学,2007.

[11] 王英玉,姚卫星.材料多轴疲劳破坏准则回顾[J].机械强度,2003,25(3)：246-250.

[12] 姚卫星.结构疲劳寿命分析[M].长沙：国防科技图书出版社,2003.

[13] 郭平.基于场强法的焊接接头疲劳寿命预测及机匣寿命研究[D].南京：南京航天航空大学,2008.

[14] Bush A.Fatigue Strength Calculation[M].Switzerland：Trans.Tech.Publictions,1988.