平面并联机构与电主轴耦合系统动态性能研究*
宋方臻,冯会民,刘 慧
(济南大学机械工程学院,济南 250022)
0 引言
并联机床作为机床技术和机器人技术结合的产物,受到了国内外学者的广泛关注。制约并联机床发展的主要因素是精度问题,影响并联机床加工精度的因素有多种,已有许多的学者针对各影响因素进行了深入的研究[1-5]。Wang[1]建立了实际 Stewart平台机构的反向和前向运动学模型,用仿真的方法研究了机构制造误差对动平台精度的影响;Patel和Ehmann[2]建立了Stewart平台机构的微分误差模型。王海军[3]运用ADMAS软件建立了并联机床的并联机构的虚拟样机,通过运动仿真研究了关节间隙对并联机床加工精度的影响规律;徐轶轲[4]根据并联机构的动力学模型提出了一种控制补偿策略来减小系统的动态误差;史长虹[5]根据虚拟轴数控机床与传统数控机床的本质区别,拟订了新型变轴数控机床定姿态工作精度检验方案,并对变姿态工作精度检验提出建议。杜兆才[6]运用弹性动力学理论和 Lagrange方程推导出了平面柔性并联机器人的动力学方程,研究了杆件的弹性变形对机器人动平台的位置误差和方向误差的影响。何雪浤[7]等人研究了3-TPT型并联机床工作空间内杆长误差和铰链间隙误差对动平台运动精度的影响规律。但是,上述研究主要是针对并联机床的静态误差和准静态误差进行的,关于动态误差的研究还很不充分。实际上,并联机床的动态性能是影响其精度的主要因素之一,有必要进行深入探讨。平面并联机构、电主轴和控制系统是平面并联机床的重要组成部分。在加工过程中,平面并联机构和电主轴形成耦合的动力学系统。因此,必须从平面并联机构与电主轴耦合系统的角度出发,研究动力学参数变化对平面并联机床动态性能的影响,从而提出降低平面并联机床加工误差的有效措施。
1 耦合系统的分析模型
图1为平面并联机构与电主轴耦合系统的结构示意图。

图1 平面并联机构结构示意图(主轴置于节点C)
在文献[8]中,我们已建立了平面并联机构与电主轴耦合系统的动力学方程:

篇幅所限,动力学方程(1)中的参数和变量详见文献[8],这里不再赘述。
描述平面并联机构与电主轴耦合系统动态性能的重要参数有刚度和阻尼。平面并联机床主要由平面并联机构和电主轴构成,因此分别研究刚度和阻尼参数变化对平面并联机构与电主轴耦合系统动态性能的影响。
根据平面并联机构与电主轴耦合系统的动力学方程(1),就可以利用数值分析的方法研究参数变化对耦合系统动态性能的影响。本文研究的耦合系统实例的具体参数如下:
杆件横截面边长为a0=25mm,b0=25mm,各杆的长度为l1=l4=40mm,l2=l3=200mm,弹性模量E=210Gpa,转子质量 m=1.3kg,转子长度 l=210mm,转子两端轴承到转子质心的距离a=b=105mm。
2 刚度变化对耦合系统动态性能影响
通常以幅频特性作为评价机床动态性能的依据。因此,本文通过MATLAB[9]编程来研究刚度和阻尼变化对平面并联机构与电主轴耦合系统动态性能的影响。
(1)平面并联机构的刚度对耦合系统动态性能的影响
杆件尺寸是反映杆件刚度的重要参数,因此可以通过改变并联杆件的截面尺寸来调节并联杆件的刚度,从而研究平面并联机构的刚度对耦合系统动态性能的影响。
由于只考虑平面并联机构的面内变形,主轴在A0、B0端的振动情况是相同的[8],故仅对主轴一端的幅频特性进行研究。图2、3为并联杆件截面高度分别为25mm、35mm和45mm时,主轴在x、y方向上的幅频特性曲线。

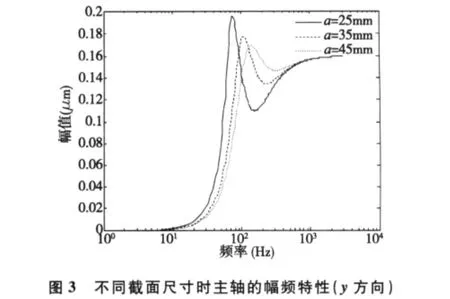
从以上两图可以看出,截面尺寸变化对主轴A0端的振动响应产生了显著的影响。当截面高度由25mm增加到35mm时,A0端在 x方向的振幅由原来的0.32μm减小到0.25μm,即振幅减小了21.9%,在y方向上的振幅减少到0.18μm,减小了10%;同时可以看出,截面尺寸的变化对耦合系统的固有频率也有一定影响。
(2)主轴刚度对耦合系统响应的影响
主轴的刚度kxa变化对耦合系统动态性能的影响如图4、5 所示(图中 kxa1、kxa2、kxa3为 kxa的三个不同取值):


从图4、5中的数据可以看到,主轴刚度kxa变化对耦合系统振动响应的影响不明显。当主轴刚度增加到原来的1.2倍、1.4倍的时候,其振幅基本不变,仅在频率为100Hz时略有变化。
3 阻尼对平面并联机构与电主轴耦合系统响应的影响
(1)平面并联杆件的阻尼对耦合系统响应的影响
图6、7为平面并联杆件的阻尼c变化时,主轴在x、y方向上的振动响应曲线(图中c1、c2、c3为c的三个不同取值,c为比例阻尼,[k]为并联杆件系统的刚度矩阵)。
从上面两图中可以看出,并联杆件的阻尼参数c对耦合系统振动的影响非常显著。阻尼增大为原来1倍的情况下,主轴在x方向上的振幅由原来的0.32μm减小到0.16μm,减小了50%,在y方向上的振幅也由原来的0.195μm减小到0.13μm,减小了33.3%。
(2)主轴阻尼对耦合系统响应的影响
下面研究主轴的阻尼cxa变化对耦合系统的动态性能产生的影响。图8、9为主轴的阻尼发生变化时,主轴在x、y方向上的振动响应(这两幅图中c1、c2、c3为cxa的三个不同取值)。


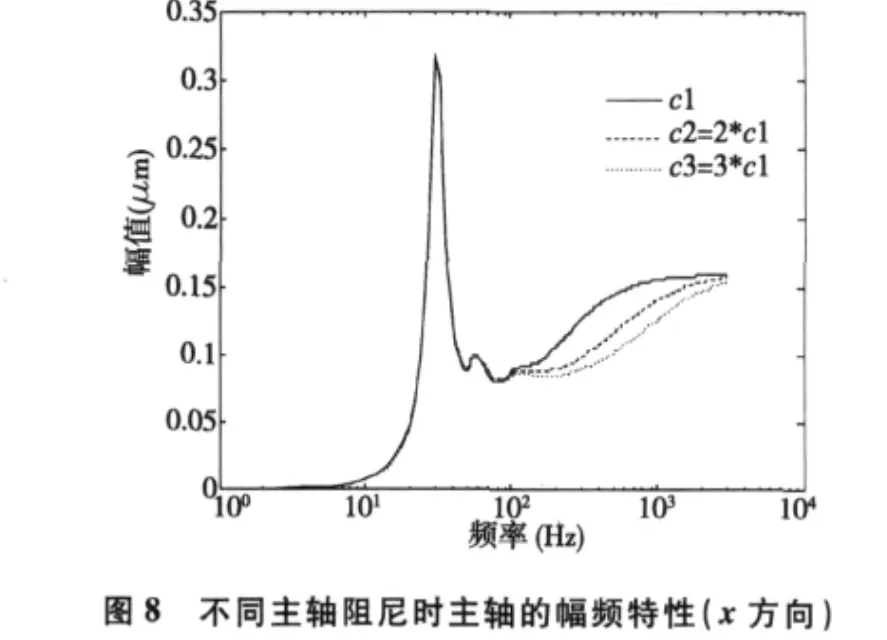

从上面两图中的数据显示可以看出,主轴阻尼cxa变化对耦合系统的振动影响不是很明显,尤其是主轴在x方向上的振幅基本没有发生变化,仅在频率大于100Hz时略微有些差距;在y方向上主轴的振幅变化比x方向上要明显,主轴阻尼增大1倍情况下,幅值大约降低0.03μm,即降低了15.4%。
由此可以得出,平面并联杆件系统的阻尼变化对耦合系统的振动影响较为明显,主轴阻尼变化对耦合系统振动的影响不如杆件系统阻尼的影响大。因此选择增大平面并联杆件系统的阻尼参数是提高平面并联机床加工精度的另外一条可行措施。例如,可以采用阻尼层技术,这样即不会使杆件尺寸显著增大,又能使机床主轴达到减振的效果。
4 系统的瞬态响应
结构在给定载荷激励下的瞬态响应是评价其动态性能优劣的重要指标。在不同的刚度和阻尼情况下,观察脉冲信号激励作用下主轴的运动轨迹,更能直观体现平面并联机构与电主轴耦合系统的动态性能。
(1)刚度变化对主轴运动的影响
当杆件截面高度为25mm,主轴刚度为428750N/m时主轴的运动轨迹如图10所示。仅将杆件截面高度改变为35mm,保持主轴刚度不变,得到的主轴运动轨迹如图11所示。而保持杆件截面高度为25mm不变,将主轴刚度改变为图10所对应刚度的1.2倍,得到的主轴运动轨迹如图12所示。



图12 杆件截面高度为25mm,主轴刚度增大1.2倍后主轴的运动轨迹
从图10、11、12可以看出,当截面高度由25mm增大到35mm时,主轴的振动范围有了明显的降低:在x方向上由原来的0.065μm减小到0.05μm,振幅降低了23%,在 y方向上由原来的 0.036μm降低到0.03μm,降幅为16.7%;而当主轴刚度变化时,主轴的振动范围变化不明显,振幅在x方向仅减小0.002μm,在y方向上仅减小0.001μm。
(2)阻尼变化对主轴运动的影响
当将杆件阻尼增大到图10所对应阻尼一倍,保持系统其它参数不变,得到的主轴运动轨迹如图13所示。而保持系统其它参数不变,仅将主轴阻尼改变为图10所对应阻尼的一倍,得到的主轴运动轨迹如图14所示。


将图13、14与图10中的数据对 比可以看出,当杆件阻尼增大为原来的一倍时,主轴的振动范围变化明显:在x方向上振幅减小了0.004μm,减幅比为6%,在y方向上的振幅减少了8%;相比较而言,当主轴阻尼增大为原来的一倍时,主轴的振动范围变化不大,振幅在x方向仅减小了0.003μm,在y方向上几乎无变化。
5 结束语
在平面并联机构与电主轴耦合系统动力学模型的基础上,分别研究了平面并联机构及主轴的刚度和阻尼参数变化对耦合系统的动态性能响应规律。结果表明,耦合系统的动态性能主要受平面并联杆件的刚度和阻尼的影响,平面并联机床的加工精度随并联杆件截面尺寸(刚度)的增大而提高,相比较而言,受主轴的刚度和阻尼变化的影响较小。因此,在提高平面并联机床的加工精度和动态性能时,应该着重考虑平面并联机构,适当地增大并联杆件的刚度(例如增大杆件的截面尺寸)和阻尼。
[1]Jian Wang,Oren Masory.On the Accuracy of a Stewart Platform-Part I the effect of Manufacturing Tolerances.IEEE,1993:114-120.
[2]A.J.Patel,K.F.Ehmann.Volumetric Error Analysis of a Stewart Platform-Based Machine Tool.Annals of the CIRP,1997,46(1):287-290.
[3]王海军,王君英.关节间隙对并联机床精度的影响规律研究[J]. 中国机械工程,2007,18(4):470-474.
[4]徐轶轲,刘强.两自由度并联机构动力学分析及其控制补偿策略[J].制造业信息化,2006(2):113-114.
[5]史长虹,张建民,张同庄,等.变轴数控机床重复定位精度评定策略探讨[J].北京理工大学学报,2001,21(4):450-453.
[6]杜兆才,余跃庆,张绪平.平面柔性并联机器人动力学建模[J]. 机械工程学报,2007,43(9):96-101.
[7]何雪浤,张敏,谢里阳,等.3-TPT型并联机床的精度分析与仿真[J]. 中国机械工程,2008,19(11):1336-1339.
[8]刘慧,宋方臻,冯会民,等.平面并联机构与电主轴耦合系统动力学分析[J].组合机床与自动化加工技术,2010,437(7):12-16.
[9]王正林,刘明.精通MATLAB 7[M].北京:电子工业出版社,2006.

