水下滑翔机建模与运动PID控制

张福斌, 汪 刚 , 陈宇航, 鲍鸿杰



水下滑翔机建模与运动PID控制

张福斌1,2, 汪 刚1, 陈宇航1, 鲍鸿杰1

(1.西北工业大学 航海学院, 陕西 西安, 710072; 2.水下信息处理与控制国家级重点实验室, 陕西 西安, 710072)

水下滑翔机是一种浮力驱动的新型水下航行器, 其特殊的驱动方式和结构特点增加了建模和控制分析的复杂度。为获得准确有效的水下运动控制方法, 本文通过滑翔机运动学和动力学分析, 建立了较为完善的3D空间数学模型, 并进行了合理的假设和简化, 得到纵平面内小扰动线性化模型。在此基础上, 设计了比例积分微分(PID)控制器。并针对滑翔机的纵平面运动进行了仿真分析, 结果显示, PID控制器有很好的干扰抑制能力和跟踪性能, 由此也验证了纵平面内滑翔机的运动特性。

水下滑翔机; 比例积分微分控制器(PID); 动力学模型; 线性化模型

0 引言

水下滑翔机是一种新型自主式水下航行器(autonomous underwater vehicle, AUV), 它具有水平固定翼和尾翼, 可通过浮力控制装置及内部移动质量块来控制和调节浮力及姿态以实现水下纵平面的锯齿形滑翔运动, 并通过操舵或改变横滚姿态实现转向[1]。与传统水下航行器相比, 它具有机动灵活性强、噪音小及续航力强等特点。可应用于军事情报收集、侦察、监视、网络中心战、环境监测、生物观察及水体特性调查等方面。水下滑翔机可单独工作也可组群协作, 并由远程控制或根据实时数据进行任务使命的自适应调整。

自20世纪末, 美国、法国、加拿大和日本等先后对水下滑翔机展开了深入研究, 促使其技术有了较大发展。Nina等人针对基于由横滚控制转向的模型对滑翔机的运动机理和控制特性作了分析[2]。 Naomi等人针对ROGUE试验级滑翔机的纵平面运动特性有较详细的分析[3-4], 其模型中移动质量块具有2个自由度, 由于移动质量块与滑翔机运动的横滚耦合, 即使在滑翔机的稳态情况下, 滑块位置仍然会受滑翔机的运动影响较大。

本文基于SLOCUM滑翔机建立模型[4], 采用单自由度移动质量块及尾舵来控制俯仰和转向, 建立了滑翔机的3D空间运动学和动力学模型, 并推导了纵平面内滑翔机运动简化模型, 在此基础上, 设计了水下定角滑翔的比例积分微分(proportional integral differential, PID)控制律, 验证了PID控制对滑翔机的控制效果。

1 水下滑翔机的建模

1.1 坐标系定义

1.1.1 地面坐标系o-xyz

1.1.2 载体坐标系-

载体坐标系的原点选在滑翔机的几何中心,轴沿着滑翔机的纵轴指向头部方向,轴沿着滑翔机的横轴指向右,轴沿着滑翔机的立轴指向下, 3个坐标轴组成右手直角坐标系, 如图1所示。

图1 水下滑翔机的坐标系定义

1.2 基本假设

水下滑翔机为刚体, 其外形关于纵平面和水平面对称; 滑翔机浸没在流体介质中, 处于完全沾湿状态; 流体动力位置力及阻尼力满足线性假设; 载体坐标系原点与滑翔机的浮心重合, 并近似地认为地面坐标系为惯性坐标系[6]。

1.3 滑翔机各模块质量定义

滑翔机的总质量

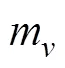
绕浮心的固定质量的惯性张量

体坐标系向地面坐标系的旋转矩阵

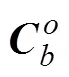
地面坐标系下滑翔机的位置

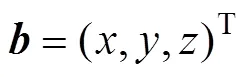
体坐标系下的速度

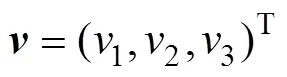
体坐标系下的角速度

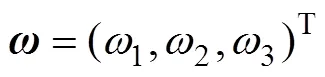
1.4 滑翔机的运动学方程

平动运动学方程

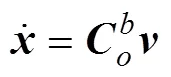
转动运动学方程

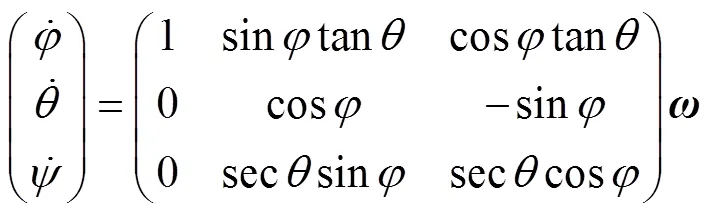
1.5 作用在滑翔机上的力

1.5.1 理想流体作用力

且

1.5.2 流体黏性位置力

流体黏性位置力及力矩在载体坐标系下分量

1.5.3 流体黏性阻尼力

流体黏性阻尼力及力矩在载体坐标系下分量

1.5.4 浮力

浮力在载体坐标系下的分量

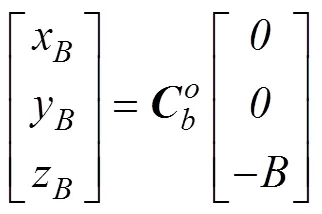
式中:为滑翔机所受到的浮力。

1.5.5 重力

重力及重力矩在载体坐标系下的分量

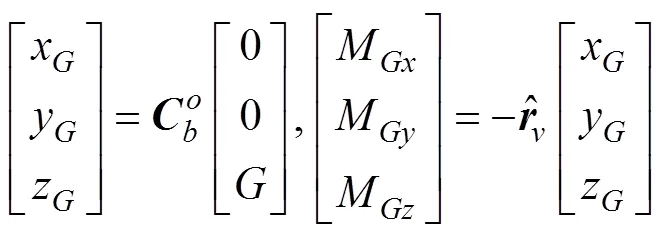
1.6 滑翔机的动力学方程

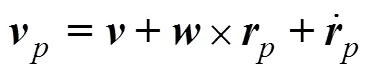
其动量和动量矩矩阵为

滑翔机流体动力系统的动量及动量矩写成矩阵

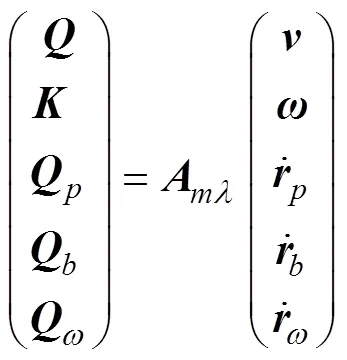
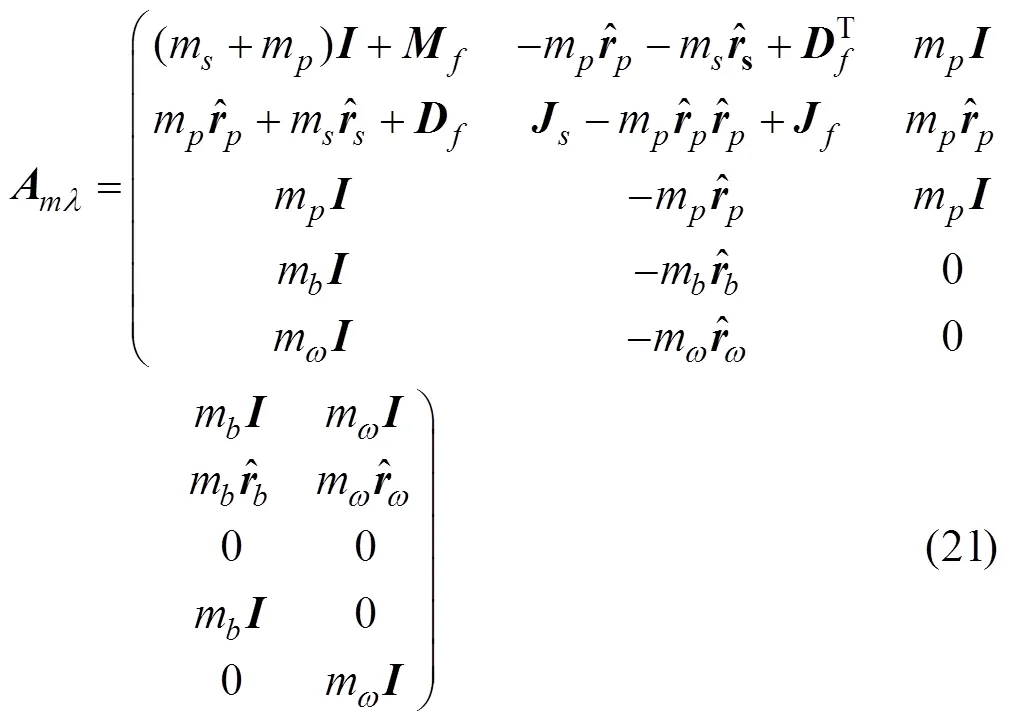
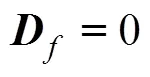
由假设条件可知, 质量矩阵

惯性张量矩阵

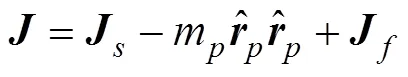
滑翔机动力学方程组根据动量和动量矩定理建立, 在体坐标系中可表示为

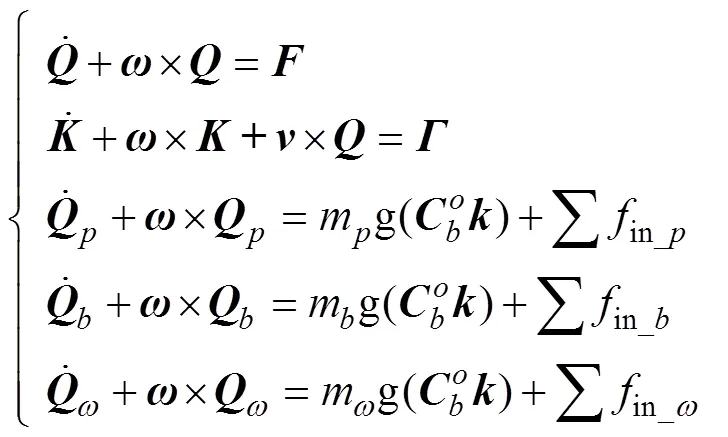
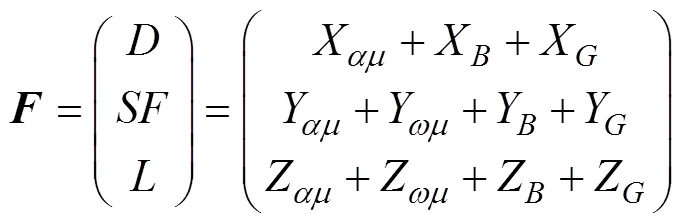
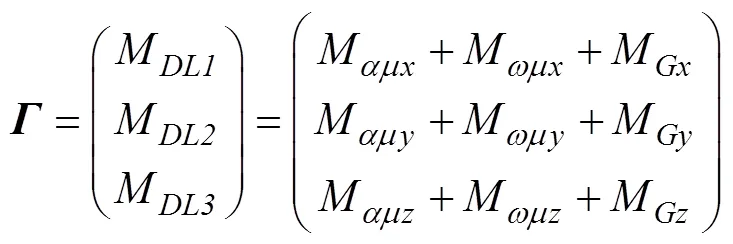
对式(18)两边求导得

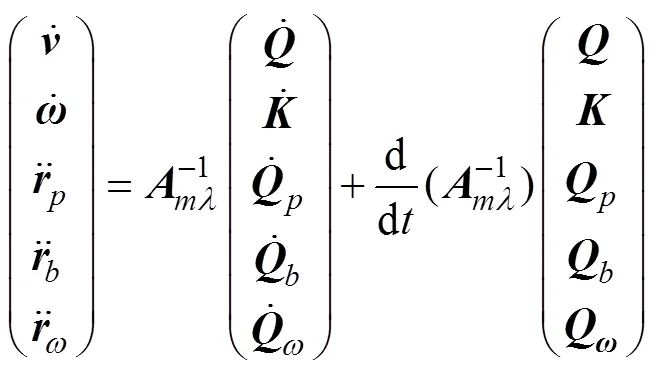
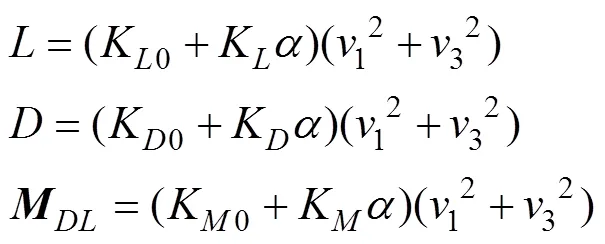
令

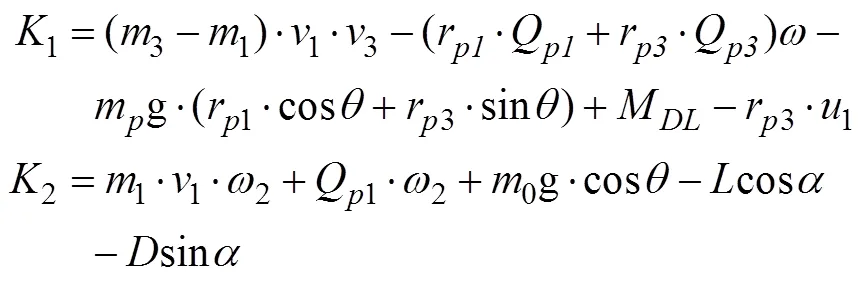
从而得滑翔机在水下纵平面的数学模型

2 纵平面内的稳态滑翔

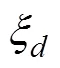
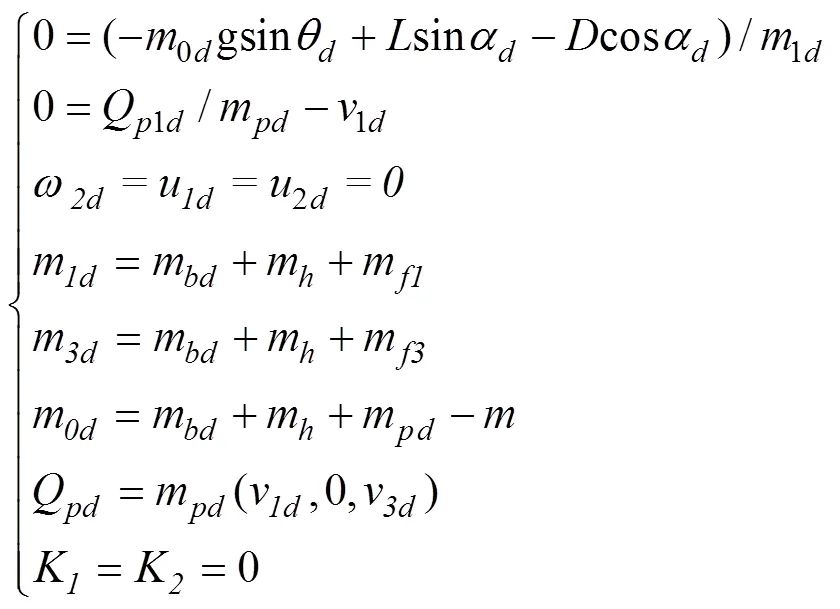
由公式(31)可以计算出稳态滑翔稳态参数, 并且能够得到该平衡点附近的小扰动线性系统。

3 控制器设计

本文拟通过基于过程控制的PID控制器设计方法进行控制器的设计, 分析滑翔机在纵平面内的运动控制问题。

图2 水下滑翔机PID控制系统

选取系统的状态向量和控制输入向量为

对滑翔机纵平面模型式(30)在平衡态处线性化, 得到小扰动线性化模型

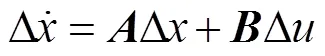
3.1 系统的控制变量选择

3.2 PID控制器设计

实际过程控制中, PID控制器的数学模型为[8]

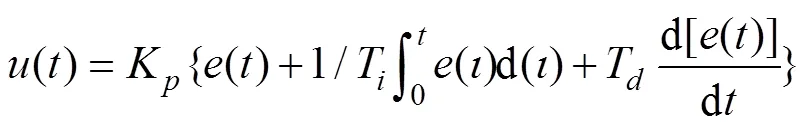
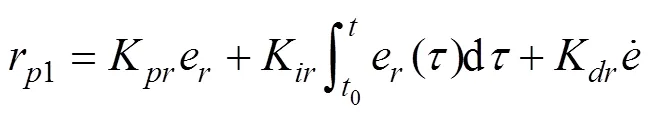
4 仿真结果

4.1 滑翔机下潜过程中PID控制仿真

假设滑翔机预先处于-43°滑翔角, 速度0.37 m/s的稳定滑翔状态, 现在欲将其控制在-27°滑翔角, 速度0.34 m/s的稳定状态下, 并航行到定深20 m, 其滑行轨迹如图3所示。图中和分别为滑翔机下潜的深度和前向位移。选取K=20,K=2,K=3.8,K=10,K=1.2,K=2.2为PID的加权系数。仿真结果显示, 从第0 s的时候, 滑翔机在PID控制器的作用下开始向设定状态运动, 经过约30 s左右的时间达到预定状态,滑翔机滑翔角, 横滚角2, 速度均收敛到预定状态, 控制结果具有很好的指令跟踪响应性能。如图4所示。

图3 滑翔机下潜过程中纵平面航行轨迹

图4 滑翔机下潜时对指令的跟踪响应

4.2 滑翔机下潜过程中滑块的运动仿真

在4.1节的仿真条件下, 控制滑翔机俯仰运动的滑块能迅速收敛到稳态值0.02 m。仿真结果如图5所示。控制输入激励1=Δr也能迅速收敛, 如图6所示。

从仿真图形中可以看出, 滑翔机通过调节作用在移动质量块上的控制力可以快速地改变状态, 及时对控制指令实现跟踪响应, 最后状态稳定到定角稳态滑翔, 仿真图与实际的滑翔机纵平面运动情况相符。

图5 滑翔机下潜时滑块的跟踪响应

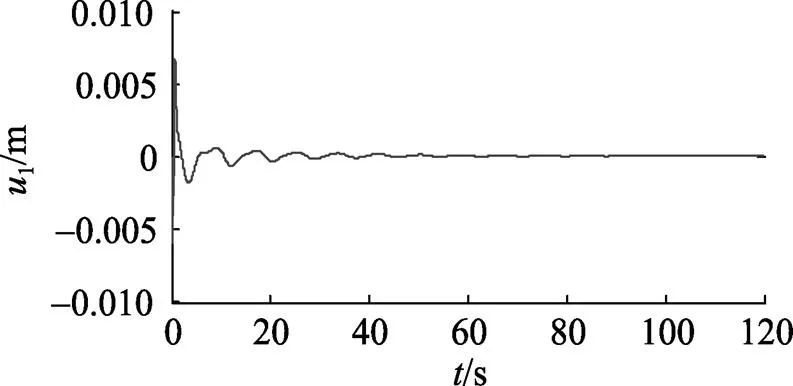
图6 滑翔机下潜时控制输入变化

5 结束语

本文给出了较为完整的水下滑翔机3D空间的模型, 根据小扰动原理简化得到纵平面内的数学模型中, 将移动质量块限制在轴方向运动,,轴方向固定, 分析了滑翔机在纵平面内的运动特性, 在此基础上设计了PID控制器, 并分析控制结果。仿真结果显示, PID控制取得了良好的控制效果。

[1] Jenkins S A, Humphreys D E, Sherman J, et al. Underwater Glider System Study [R]. UC San Diego: Scripps Institution of Oceanography, 2003.

[2] Mahmoudian N, Woolsey C. Underwater Glider Motion Control[C]//Proceedings of the 47th IEEE Conference on Decision and Control, 2008.

[3] Joshua G G. Underwater Gliders: Dynamics, Control And Design[D]. Princeton University, 2005.

[4] Joshua G G, Naomi E L. Underwater Glider Dynamics And Control[C]//12th International Sym- posium on Unmanned Untethered Submersible Technology, 2001.

[5] 严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.

[6] 徐德民. 鱼雷自动控制系统[M]. 西安: 西北工业大学出版社, 2006.

[7] 陈宇航.水下滑翔机建模与控制研究[R].西安: 西北工业大学,2009.

[8] 薛定宇. 控制计算机辅助设计[M]. 北京: 清华大学出版社, 2007.

Modeling and PID Control of Underwater Glider Motion

ZHANG Fu-bin1,2, WANG Gang1, CHEN Yu-hang1, BAO Hong-jie1

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China；2. National Key Laboratory for Underwater Information Processing and Control, Xi′an 710072, China)

Underwater glider is a new kind of autonomous underwater vehicle driven by buoyancy force, however its special drive mode and structural characteristics increase the complexity of modeling and control analysis. To obtain an accurate and efficient control strategy for underwater motion, a complete three-dimensional mathematical model is built by analyzing kinematics and dynamics of the glider via some reasonable assumptions and simplification, thus a small disturbance vertical plane linear model is achieved. On this basis, a proportional integral differential (PID) controller is designed. In addition, the vertical plane motion of the glider is simulated. The simulation results verify the vertical plane motion characteristics of the glider using the PID controller, and demonstrate its better disturbance resistance and tracking performance.

underwater glider; proportional integral differential (PID) controller; dynamic model; linearization model

TJ630; V277; TP273

A

1673-1948(2011)02-0114-06

2000-00-00;

2010-07-27.

水下信息处理与控制国家级重点实验室基金(9140C230503090C23)

张福斌(1972-), 男, 副教授, 主要研究领域为水下航行器导航与控制技术.

(责任编辑: 杨力军)