基于性能退化数据的锂离子电池贮存可靠性评估方法

黄 燕, 宋保维, 谢亚丽



基于性能退化数据的锂离子电池贮存可靠性评估方法

黄 燕, 宋保维, 谢亚丽

(西北工业大学 航海学院, 陕西 西安, 710072)

大功率锂离子二次电池在贮存过程中通常出现失效数较少但性能退化较普遍的现象, 而且测量所得的电池数据不确定和不完整。为评估电池贮存可靠度, 该文提出了一种根据正常电池数据建立模糊隶属函数处理不完整数据的方法, 通过该方法得到电池的贮存可靠度。通过多组数据计算, 证明了该方法的有效性和实用性。

大功率锂离子二次电池; 贮存可靠度; 模糊隶属函数; 可靠性评估

0 引言

锂离子蓄电池是20世纪90年代问世的一种新型蓄电池, 该电池以其比能量高、工作电压高、循环周期长、放电时间长、充电时间短、搁置时间长和使用环境恶劣等优点赢得了电源动力工作者的青睐。进入21世纪后, 各国都致力于将这种电池用于军事领域。在国内, 大功率锂离子二次电池是近3、4年才开始运用的新产品, 对于这项新技术的许多特性还在不断的总结与摸索之中。

由于自放电现象的存在, 在一段时间的贮存后, 电池电压显著降低, 荷电量减少。由于制造质量等原因, 一些单体电池电压下降尤为严重, 明显低于电池组中的其他电池。如果在贮存过程中发现少量电池电量下降, 可通过维护来恢复, 而一旦在搁置过程中出现这种情况, 则会因为电池使用前没有维护或补充充电过程而导致任务不可靠。按常规可靠性概念, 需在电池发生失效时才计为可靠性计算数据, 而出现电量下降的电池并没有失效, 却确实影响着任务, 这显然不符合真实情况。锂离子二次电池随着贮存时间加长、质量差异、循环使用次数增多、滥用情况的发生等因素会导致其荷电性能下降, 使对锂离子二次电池贮存可靠性的研究更加复杂。怎样评估锂离子二次电池的贮存可靠度是本文研究的主要问题。

近几十年来, 很多工程技术人员和统计学者试图通过产品性能退化数据进行可靠性分析, 并在理论研究和工程应用上取得了初步成功[1-3]。基于性能退化数据的可靠性分析理论研究已逐步成为可靠性研究的新方向。性能退化分析相对于传统的可靠性分析, 对信息的利用更加全面, 避免了数据的损失, 在一定程度上提高了分析精度。本文主要针对氧化钴锂锂离子二次电池在贮存过程中较常见的贮存后荷电性能退化的问题展开分析研究, 运用性能退化理论和模糊理论研究电池的贮存可靠性。

1 锂二次电池在使用、贮存中存在的问题

研究的氧化钴锂锂离子二次电池是以某种材料为负极、以氧化钴锂为正极的电池, 化学反应式为

电池中的锂离子由正极供给, 所以正极材料中的锂离子决定着电池的容量, 材料的结构决定电导率、放电速率和性能。负极能嵌入多少锂离子也决定了电池的容量, 储锂能量越高, 电池的能量越大。

对锂离子二次电池出现荷电能力降低的情况, 定义: 二次电池在规定的贮存时间段内, 正常工作条件下的放电量应大于等于规定的电量, 否则为性能发生了退化。

为了保证用电设备能正常工作, 需要准确和可靠地检测电池的荷电状态(即剩余电量), 但要准确量化电池的退化情况是较困难的, 有如下原因。

1) 电池性能退化与电池内部发生的复杂化学反应有关, 从微观的角度是无法进行荷电状态的工程量化的。

2) 在某一状态下, 电池中还有多少剩余电量是与放电电流、电压、温度和充放电历史相关的[4], 无法用一个明确的方程式表示。

3) 在整组电池中出现了性能发生退化的单体电池时, 由于单体电池间存在互充电现象, 已发生性能退化的电池往往在检测时显示虚假的高电压值, 因此, 通过简单的测量难以判断单体电池的性能是否退化, 退化了多少。

确认二次电池发生退化的方法为: 将整组电池恒流放电, 过程中不断采集每只单体电池的电压数据, 当某只单体电池的电压渐渐低于其他电池, 并在某一时刻电压迅速下降至极限电压min以下, 则可确定该单体电池发生了性能退化。通常二次电池的电压一旦低于极限电压, 电池就会发生失效, (锂二次电池在失效前属可修产品, 经维护后退化电池可趋于正常。)显然, 使用这种方法会造成电池的失效, 为了找出发生退化的电池而将其损失掉是得不偿失的。

在工程实际中, 仓库贮存条件下对电池进行定期维护时, 一般对电池组反复进行放电—充电。由于每只单体电池的充放上、下限电压等性能指标不一致, 无法预先设定准确的充放电上、下极限电压。为避免损失, 一般根据经验选定一个值截止作为放电截止值, 该值大于极限电压min, 只要整组电池中有一只单体电池的电压下降到截止电压时即停止放电, 该过程基本杜绝了电池失效。在充、放电的同时进行电压值的检测和记录。通过这样的检测可以得到大量电池放电数据。但要注意, 这样得到的数据是不完整的, 因为当某单体电池到达截止电压时, 可能还有很多退化程度稍低的电池未显露出来。

在电池实际使用时, 由于电池管理(监控)设备较庞大而不可能随使用设备携带, 如: 电动汽车、水下航行器等不可能对单体电池进行监控, 无法对其实施自动断电保护, 所以个别性能退化严重的单体电池可能会在执行任务过程中因过放而失效。

在工程实际中还存在以下一些不确定问题。

1) 在国内现有电池生产水平下, 单体电池质量一致性较差, 在随机抽取单体电池组成电池组时, 有些电池组中可能存在多只性能较差的电池, 有可能在维护放电刚开始即有一只特差的电池到达了截止电压, 使放电中止, 于是整组电池中可能还有多只问题电池未暴露; 从现有数据来看, 根本无法了解在一组电池中到底存在多少只已退化单体电池。

2) 由于制造原因, 单体电池的初始电量和放电极限电压不确定, 导致正常电池组的放电数据差异较大, 不能确定电池组标准的充放电时间, 只能凭人工经验在充放电时具体确定。

3) 放电时电流与放电系统阻值和温升有关, 不可能准确地恒流, 用放电时间长度表征放电量亦带有不确定性。

4) 进行电池组设计时, 一般会留有几只单体电池的余量。例如, 允许有2.5%的电池彻底失效, 其余为满电, 才可保证完成任务。似乎该条件可作为电池组完成任务能力的判据, 但实际情况是, 经贮存后, 同组电池中单体电池彻底失效的情况极少, 而全体单体电池电压均有下降, 且各不相同, 使得电池可靠度判定存在不确定性。

2 电池放电数据的模糊处理

对于上述不确定问题, 工程实际中通常运用模糊理论进行处理[5]。一般采用模糊隶属度对锂二次电池荷电性能的退化程度进行量化, 主要思路如下。

1) 先总结正常电池组的放电数据规律, 得到正常电池组的荷电模糊特征函数。

2) 将需要判断的电池组数据带入进行计算(包括放电过程中中止放电, 或是状态不明确的), 得每组电池对正常电池特征的模糊隶属度。

3) 将各种隶属度综合得到电池组对于正常电池状态的隶属函数。

以下函数是通过对1万多只单体电池满电贮存3个月后, 在规定放电条件下的正常电池检测数据总结得到的模糊特征函数。

其图形见图1, 带入电池组数据即可得模糊特征值。

其图形见图1。

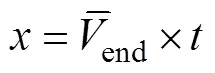
其图形见图1。

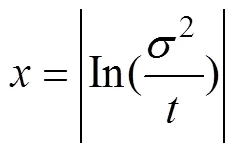
其图形见图1。

需要注意的是, 在不同的种类、贮存时间和充电状态(例如满电状态或充1/3电量)时, 以上函数的取值会有所不同, 可根据专家经验调整模糊特征函数中的参数来适应变化。

取域值, 当()≥时, 即为满足要求的电池组。

3 基于性能理论的可靠性评估

由性能可靠性理论, 产品技术性能的失效按故障性质可分为2类: 一类是由突变性故障引起的突发性失效; 一类是由渐变性故障引起的退化性失效。其中, 渐变失效模式用于计算性能可靠度, 产品的可靠度是上述2种可靠度的综合。文献[3-5]指出, 产品可靠度(产品所有性能指标可靠性的综合)定义: 产品不发生突发性和退化性失效的概率, 记为, 表达式=R·R,其中,R为产品不失效的概率;R为不发生退化性失效的概率。产品的性能指标一般以如下形式给出。

2) 下限型:≤r

3) 上限型:≥r

4) 双限型:≤r≤

由于通过检测无法得到电池准确的荷电量数据, 而由()的构成可知, 该参数模糊表征了电池组的荷电能力, 故取()为电池荷电性能参数进行性能可靠度计算, 由于导致电池荷电性能退化的因素较多, 如制造原因、原材料、装配、搁置时间长短、使用频度、环境和电流等。电池组批量足够大时, 隶属函数值变化呈正态分布。计算时可先剔除异常数据, 进行分布检验, 求解全部电池组的隶属函数及其正态分布平均值和标准差, 然后通过正态函数积分得到该批电池的贮存可靠度计算结果。()≥≥0为下限型, 其性能可靠度计算公式为

4 实例分析

为了验证本文方法的普遍适应性, 得到电池可靠度随贮存次数、批次不同而变化的规律, 试验采用不同批次、不同维护次数的电池; 同时, 为检验算法是否能区分出不合格的数据, 特加入9组不满足贮存条件的电池。具体情况如下：

A组: 常规组, 满电状态贮存3个月后进行维护时的数据。从批次1抽取50组、批次2抽取6组, 批次3抽取6组。

B组: 非常规组, 1/3电量状态经半年贮存后进行维护数据。从各批次中抽取, 共9组。

每组电池含90只单体电池, 每只单体电池数据90~120个。限于篇幅, 这里略去原始数据。

将以上数据带入式(1)～式(5)计算, 计算步骤如下。

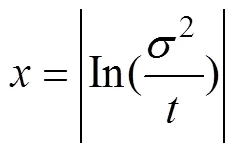
表1 批次1电池第1次维护数据隶属度

表2为批次1第2次维护数据的计算结果。

表2 批次1第2次维护数据隶属度

性能可靠度为

批次1第1次满电搁置3个月后, 无单体电池失效,R=0.999 6, 该50组电池综合可靠度为

1次=R×R=0.9974×0.9996=0.997 (9)

带入批次1第2次维护数据, 计算得性能可靠度R=0.952 5。

此次有7只单体电池失效,R=0.995 46, 得

2次=R×R=0.9482 (10)

带入批次2第3次维护数据, 计算得

3次=R×R=0.9947 (11)

该数据比2次大, 这是由于电池的批次不同, 质量情况不同造成。可见, 制造质量是决定电池可靠度的重要原因。

传统方法对照计算。用取自不同批次的4组电池连续贮存7～8个月、6组电池贮存5个月后检测, 仅观察其有无失效单体, 并按失效单体电池数计算该2组电池组的可靠度分别为0.99663和0.996 62。但根据实际经验, 贮存(搁置)期超过5个月的电池, 其荷电量已大大降低, 如不进行维护而直接用于任务, 将会在任务过程中出现大量失效单体电池, 影响任务完成, 其可靠度不应该有0.996 6这么高。因此, 不考虑性能退化因素计算出的贮存(搁置)可靠度值是不符合实际的。

实际执行任务后对照计算。为验证电池的实际搁置可靠度, 采用6组来自批次1、批次2、批次3的电池满电搁置3个月后执行任务, 按执行任务后失效单体电池数计算电池组执行任务的可靠度为0.996 47, 与第1次维护后用本文方法计算的结果0.997接近。说明本文提出的方法具有一定的可信性。

5 结束语

由对照计算的情况看, 用失效电池数据计算电池组的贮存(搁置)可靠度的方法, 由于没有考虑性能发生退化的情况, 计算结果过于保守。考虑了性能退化的贮存可靠度计算结果较符合实际情况。该方法可推广运用到无损检测所得数据不完整、失效数据少、性能退化情况下的贮存(搁置)可靠度评估。

[1] Jossen A, Spath V, Doring H, et al. Reliable Battery Operation—a Challenge for the Battery Management System[J]. Journal of Power Sources, 1999, 84(2): 283- 286.

[2] 胡超斌.性能可靠性评价指标的初步探讨[J],可靠性与环境适应性理论研究, 2004, 12(6):27-30. Hu Chao-bin. Researching of Measures of Performance Reliability[J]. Researching of Reliability and Environ- mental Adaptability, 2004, 12(6): 27-30.

[3] 黄建新, 边亚琴, 张胜涛, 等. 新型雷达装备系统性能可靠性评估[J], 空军工程大学学报, 2008, 9(5): 57-61. Huang Jian-xin, Bian Ya-qing, Zhang Sheng-tao, et al. The Evaluation of the Performance Reliability of New Type Radar Equipment System[J]. Journal of Air Force Engineering University (Natural Science Edition), 2008, 9(5): 57-61.

[4] 舒服华. 基于最小二乘支持向量机的电池剩余电量预测[J]. 电源技术, 2008, 32(7): 452-455. Shu Fu-hua. A Prediction Model for Remaiming Capa- city in Batteries Based on Least Square Support Vector Machine[J].Electrical Source Technic, 2008, 32 (7): 452-455.

[5] 李正, 宋保维, 梁庆卫, 等. 基于模糊可靠度确定长贮装备检验周期的方法[C]//2003年全国机械可靠性学术交流会论文集, 2003: 90-91. Li Zheng, Song Bao-wei, Liang Qing-wei. A Method of Ensuring Material Testing Period Based on Fuzzy Relia- bility[C]//The Proceedings of Mechanical Reliability Convention in China 2003, 2003: 90-91.

A Storage Reliability Evaluation Method of Lithium Battery Based on Capability Degenerate Data

HUANGyan, SONGBao-wei, XIE Ya-li

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

The high power lithium batteries often display few failures but more energy loss in storage. Their energy parameters and metrical data are indeterminate and incomplete. In order to evaluate the storage reliability of the battery, this paper presents a method, in which a fuzzy membership function is established to estimate the incomplete data of the battery based on normal data. The storage reliability of the battery can be obtained with this method. Comparison of several groups of battery data proved that the method is effective and practical.

high power lithium battery; storage reliability; fuzzy membership function; reliability evaluation

TJ630.32; TB114

A

1673-1948(2011)01-0043-05

2009-10-08;

2010-03-14.

黄 燕(1968-), 博士, 主要从事水下航行器产品的质量与可靠性、维修性研究.

(责任编辑: 陈 曦)