鱼雷声引信目标回波高精度频率估计方法

谢 胜, 陈 航, 于 平



鱼雷声引信目标回波高精度频率估计方法

谢 胜1,2, 陈 航1, 于 平2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 中国人民解放军91388部队, 广东 湛江, 524022)

针对鱼雷与潜艇交会近场区体目标效应对多普勒频率估计精度的影响, 提出了一种快速高精度提取潜艇回波多普勒频率信息的频率估计方法。该方法是基于Rife算法和Quinn算法的联合频率估计方法, 充分利用Rife算法运算量小, 易工程实现的特点, 同时结合Quinn算法良好抗噪性能进行快速频率估计。针对Rife算法和Quinn算法在离散傅立叶变换(DFT)量化频率点附近估计误差偏大的问题, 采用对Rife算法和Quinn算法频率修正项进行加权的方法提高该区域的频率估计精度。仿真结果表明, 该方法计算量小、频率估计性能稳定且估计均方根误差在整个频段上比Rife算法和Quinn算法更接近克拉美-罗下限, 能较好满足反潜鱼雷主动声引信实现精确炸点预测的要求。

鱼雷; 声引信; 频率估计; Rife算法; Quinn算法; 克拉美-罗下限; 离散傅立叶变换(DFT)

0 引言

智能鱼雷在近距离攻击潜艇过程中采用垂直命中和定向聚能爆炸技术来精确打击潜艇, 确定鱼雷引信的炸点位置非常重要, 这对于目标毁伤效果有直接影响。本文基于多普勒频率进行炸点预测的原理, 针对鱼雷与潜艇交会近场区体目标效应对多普勒频率估计精度的影响展开研究。

一般来说, 衡量频率估计方法的性能主要有频率估计范围、实时性(即工程可实现性)以及估计精度3个方面。国内外不少学者提出了一些高精度频率估计的方法。如, 基于多重信号分类算法(multiple signal classification, MUSIC)、子空间旋转不变技术(estimation of signal parameters via rotational invariance techniques, ESPRIT)等现代谱分析方法虽具有频率分辨率高, 但运算量大, 不利于实时处理。而基于离散傅立叶变换(discrete fourier transform, DFT)的谱分析法采用快速傅里叶变换(fast fourier transform, FFT), 运算速度快, 易于实时处理。目前硬件可实现的正弦信号频率估计方法主要是基于FFT采用专用高速数字信号处理器(digital signal processor, DSP)芯片来实现的。常用的基于FFT插值方法有: 双线极值拟合法, 相位差法, 双线幅度Rife法, 修正Rife法(M-Rife法)[1]、结合幅度和相位的双线Quinn法等。其中Rife和Quinn法分别基于FFT主瓣内2根谱线幅度比和实部比进行插值估计频率, 仅需做一次FFT, 计算量少, 实时性好, 简单有效, 被工程实际广泛应用。本文在综合Quinn法与Rife法的优点基础上, 针对本文研究背景的实际, 结合文献[1~2]的算法思想, 提出了改进的基于Quinn法和Rife法快速高精度的频率估计方法。

1 鱼雷主动声引信炸点预测原理

图1为鱼雷攻击目标示意图。图中, 鱼雷主动声引信发射高频窄脉冲并以匀速直线运动经过固定目标, 在观测点处目标回波多普勒频移

f2f V/C (1)

其中:f为载频;为鱼雷与目标连线方向相对速度;为海水的声速。

图1 鱼雷攻击目标原理图

假定鱼雷与目标的径向距离r已给出, 若已准确估算出f, 利用多普勒频移公式可求出, 再根据图1中几何三角关系, 就可估计出观测点处脱靶量及鱼雷与目标水平距离x。图2为脱靶量=2~10 m,f=350 kHz,V=25 m/s,=1500 m/s条件下, 鱼雷从30 m处接近目标, 经过目标和远离目标的多普勒频移及其变化率。

从图2可知, 鱼雷与目标之间多普勒频移及其变化率在目标中部有很好的局位性, 利用多普勒频率信息进行炸点预测, 可望达到较高的精度。此外利用多普勒频率信息完成炸点的精确预测, 可克服回波信号幅度起伏产生的影响, 特别是多普勒频率只与鱼雷目标之间的相互运动有关, 抗干扰能力强。仿真结果表明, 该方法的预测精度主要受频率估计精度的影响。

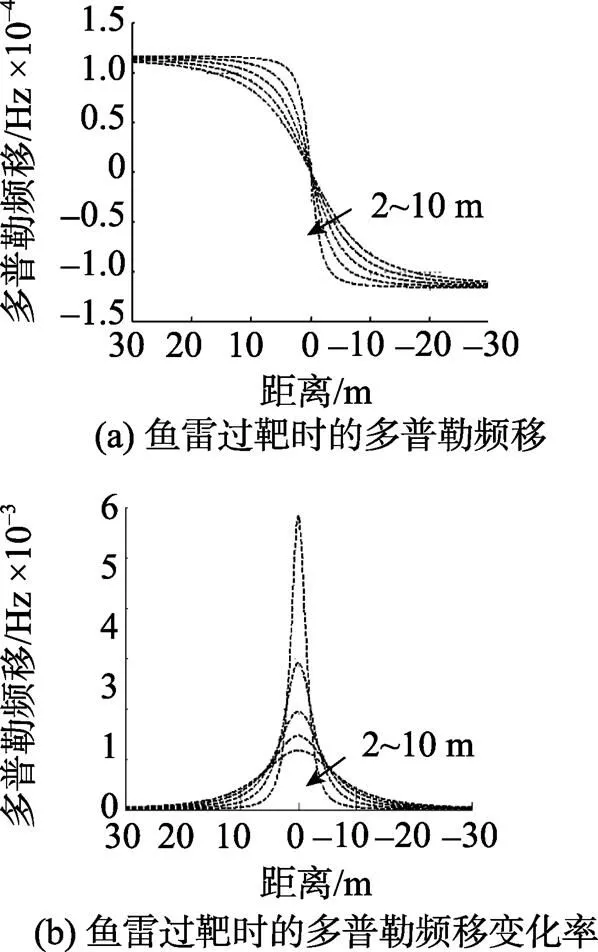
图2 鱼雷通过目标时的多普勒频移及其变化率

工作区域主要在近场区的鱼雷主动声引信所获得的潜艇回波具有显著的体目标特征, 接收信号为多个散射点(亮点)回波信号的组合,回波信号的频谱不再是单一的频率, 而是占据一定谱带的、离散且随时间变化的频谱[3-4]。亮点在距离方向上的散布造成了回波脉冲宽度的延伸, 而在方位方向上的散布造成了回波包络的变化、回波的展宽和目标强度随照射角变化等特性。潜艇亮点模型由幅度因子、频率、时延和相位跳变4个参数确定[5-6], 回波亮点的传递函数[3]

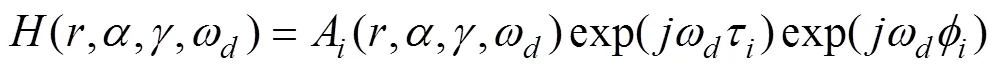
文献[6]在基于改进亮点模型基础上进一步指出, 目标运动速度和旋转角速度对回波频谱的影响最大。

综上所述, 潜艇回波亮点分布主要受声场环境、鱼雷与潜艇相对姿态以及鱼雷主动声引信发射信号参数等多种因素影响, 而且其亮点的数量是相对变化的。在不同观察点处或在某个观测时段, 目标亮点个数可能不同, 而且其多普勒频率也不同, 但不管怎样, 潜艇回波的各亮点频率都将分布在声引信载频附近的1个频段内。鱼雷声引信只要精确估计出潜艇回波各亮点多普勒频率, 就可以采用幅度区间加权等处理方法估计出最终的供精确炸点预测的目标多普勒。由于处于攻击末程, 鱼雷高速攻击目标, 因此快速实时地完成多普勒频率估计至关重要。针对上述问题, 本文提出了一种改进的快速高精度频率估计方法。

2 目标回波多普勒频率估计

2.1 改进的频率估计方法

由于在水声信号处理工程应用中, 往往只关心一个较窄高频段内的信号, 并且在固定水域的固定时间段内, 可以认为其水声环境的传播特性(比如声速传播曲线和信号的多普勒频移等)是固定不变的, 因此假设声引信接收的信号模型为

式中:A, f, 0分别为振幅、频率和初相; Δ为采样间隔;为样本数;()为实部和虚部相互独立的、方差为22的零均值复高斯白噪声。

Rife算法公式可表示如下

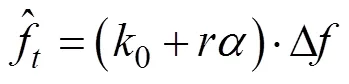
式中:为Rife法修正项;k为FFT最大谱线位置号; |(k)|为()的FFT最大谱线幅值; |(k+r)|为FFT次大谱线幅值。

式(4)、式(5)中，当|(01)≤(0-1)|,=-1, 反之=1。Δf=f/N为FFT的分辨率，f为采样频率。Rife算法特点: 当信号频率位于FFT两相邻量化频率的中心区域, 频率估计精度高, 接近CRLB; 而当信号频率位于FFT量化频率附近时, Rife算法在确定次大谱线时易受噪声干扰发生插值方向错误, 导致估计的误差急剧增加。针对Rife算法的不足, Quinn提出了利用FFT主瓣内的次大谱线与最大谱线系数复数值之比的实部进行频率插值的方法, 即Quinn法。Quinn算法见式(6)~式(10)

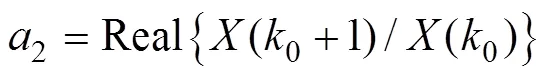
Quinn法利用了相位信息来判断插值方向, 避免了Rife法当信号频率位于DFT量化频率点附近时频率估计误差激增的问题[7]。在同等条件下Quinn法比Rife法具有更小的估计方差。Quinn法比Rife法具有更好的抗噪性能。

针对Rife法和Quinn法的优缺点, 结合两者的优点, 改进方法具体如下。

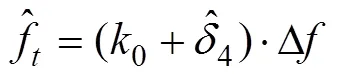
2.2 改进方法仿真与分析

为验证改进方法的正确性和估计性能, 进行计算机仿真。图1取仿真参数如下, 脱靶量为4 m, 鱼雷与目标初始水平距离X为30 m, 鱼雷速度V为25 m/s, 海水声速为1 500 m/s, 载频f为350 kHz, 采样频率f为1.4 MHz, 计算机蒙特卡罗仿真次数为1 000次。图3给出了信噪比(Signal-to-noise ratio，SNR)为3 dB和样本数为512条件下改进方法的估计频率平均值, 其中图3(b)、图3(c)是对图3(a)左右两半部分进行局部放大得到。图4给出了样本数=1 024, 不同SNR条件下Rife法, Quinn法和改进方法的估计均方根误差。对复正弦波信号, 在相位、幅度和频率3个参数均不知道的情况下, 频率无偏估计所能达到最小方差, 即估计频率方差下限——克拉美-罗下限(Cramer-Rao lower bound, CRLB)

图4 N=1 024, SNR=0 dB, 6 dB条件下Rife方法、Quinn方法和改进方法估计频率的均方根误差

从图3、图4知, 在鱼雷接近、经过或远离目标的过程中, 本文方法估计多普勒频率平均值非常接近理论多普勒值, 且估计频率的均方根误差整体上均小于Quinn法和Rife法, 估计稳定性和估计精度优于后两者。当样本数=1 024, SNR=6 dB时改进方法在攻击全程中估计频率的均方根误差最大不超过20 Hz, 接近于CRLB。

为了检验改进方法对信号频率的敏感性, 考虑到潜艇回波所有亮点频率都分布在载波频率0附近的一个频段内, 并且信号真实频率落在FFT量化频率间隔内的概率是均匀分布的, 仿真中取载波频率f= f/4 = 350 kHz, 采样频率f=1.4 MHz, 则Δf=f/N, 令f= f +δΔ,在区间[-0.5,0.5]取值均匀分成10等份, 对每个分点作1 000次蒙特卡罗仿真。为了图示简洁, 横坐标用量化频率表示, 于是f=(4)Δ。Rife法、Quinn法和改进方法在不同SNR和样本数条件下各量化频率点处的估计频率的均方根误差见图5, 图6。

由图5、图6知, 当信号频率位于DFT量化频率附近时, Rife法估计误差很大, 而在中心区域估计精度较高; Quinn法由于具有良好的抗噪声性, 估计误差比Rife法降低了很多, 改进方法利用Quinn法的这一特性并通过两者频率修正项进行加权处理的方法进一步提高了估计精度, 在整个量化频率区间内估计性能比Rife法和Quinn法更稳定, 且估计均方根误差更接近于克拉美罗下限。

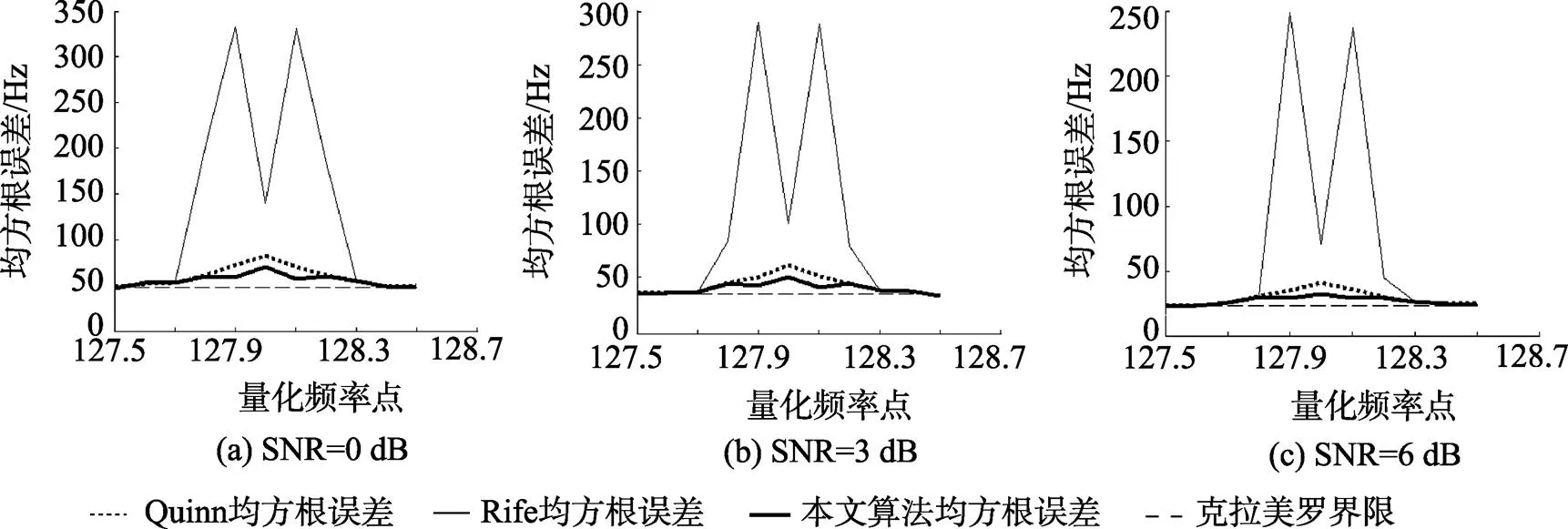
图5 N=512, NR=0 dB，3 dB,dB条件下Rife方法、Quinn方法和改进方法在整个FFT量化频率区间的估计频率均方根误差

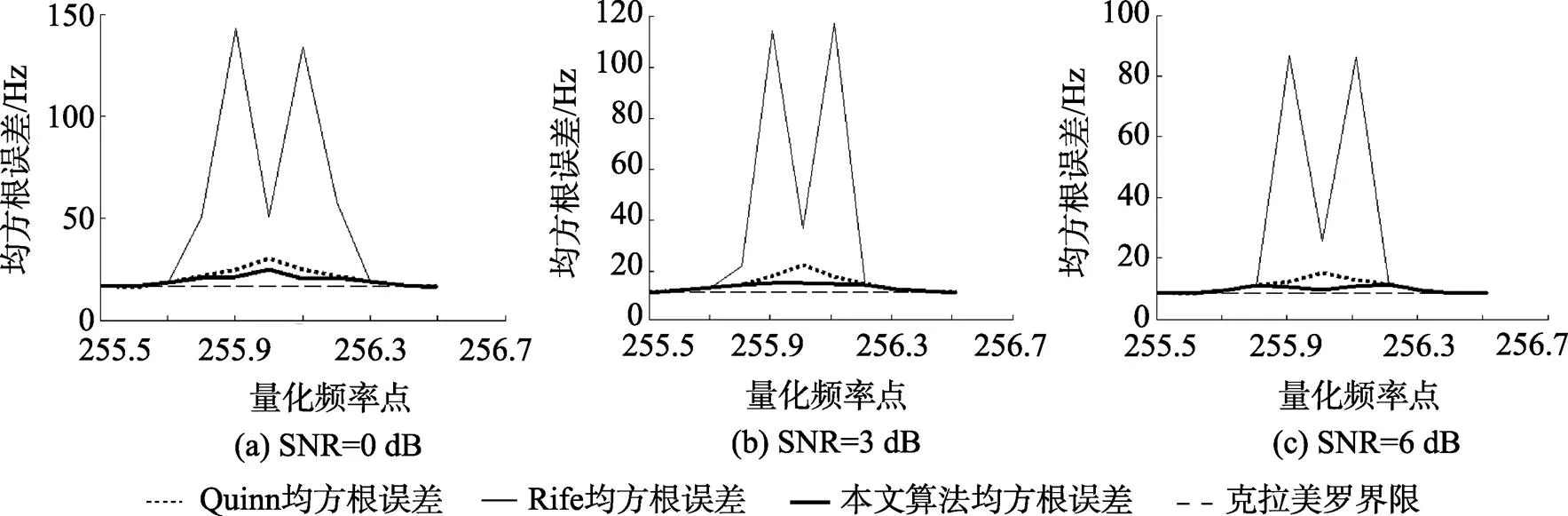
图6 N=1 024, SNR=0 dB，3 dB，6 dB条件下Rife方法、Quinn方法和改进方法在整个FFT量化频率区间的估计频率均方根误差

为检验本文方法在不同SNR条件下估计性能, 仿真条件如下: 取=512,f= 348 950 Hz,f=1.4 MHz。SNR区间为[1 dB,11 dB] , 间隔为1 dB, 每个SNR点做1 000次蒙特卡罗仿真, 见图7。图7表明, 采用改进方法时，当SNR>0 dB时估计频率均方根误差接近CRLB。

图7 不同信噪比条件下本文方法均方根误差

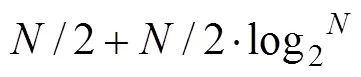
综上所述, 不论从频率估计精度、估计稳定性还是从工程易实现性, 本文方法都能较好地满足鱼雷主动声引信提取目标回波多普勒频率，实现精确炸点预测的要求。

3 结束语

基于多普勒频率实现精确炸点预测的原理, 针对鱼雷与潜艇交会近场区体目标效应对多普勒频率估计精度的影响, 本文提出了一种改进的频率估计方法。仿真结果表明, 方法估计精度高且稳健性好, 能较好地满足鱼雷主动声引信提取目标回波多普勒频率实现精确炸点预测的要求。同时, 本文方法运算量小, 易于实时处理, 具有较好的工程实用性。

[1] 邓振淼, 刘渝, 王志忠. 正弦波频率估计的修正Rife方法[J]. 数据采集与处理, 2006, 21(4): 473-477. Deng Zhen-miao, Liu Yu, Wang Zhi-zhong. Modified Rife Algorithm for Frequency Estimation of Sinusoid Wave[J]. Journal of Data Acquisition＆Processing, 2006, 21(4): 473-477.

[2]孟详儒, 李静, 陶陶, 等. Quinn和Rife-Jane方法用于振弦式传感器频率的精确检测. 数据采集与处理[J], 2008, 23(z1): 136-139.

Meng Xiang-ru, Li Jing, Tao Tao, et al. Accurate Frequency Measurement of Vibrating-Wire Sensor by Quinn and Rife-Jane Estimation[J].Journal of Data Acquisition & Processing, 2008, 23(z1): 136-139.

[3] Hao L, Paknys R. Comparison of Near-field Scattering for Finite and Infinitie Arrays of Parallel Conducting Strips TM Incidence[J].IEEE Transactions on Antennas and Propagations, 2005, 53(11): 3735-3740.

[4] 何心怡, 蒋兴舟, 林建域. 基于亮点模型的潜艇回波仿真[J], 鱼雷技术, 2001, 9(3): 15-18. He Xin-yi, Jiang Xing-zhou, Lin Jian-yu. Submarine Echo Simulation Based on Highlight Model[J], Torpedo Technology, 2001, 9(3): 15-18.

[5] 高天德, 李志舜. 水下目标亮点结构仿真技术[J]. 系统仿真学报. 2000, 3(12): 130-133. Gao Tian-de, Li Zhi-shun. Underwater Target Highlight Structure Simulation Technology[J]. Journal of System Simulation, 2000, 3(12): 130-133.

[6] 刘文远, 张静远, 吕阳, 等. 基于改进亮点模型的尺度目标建模技术[J]. 鱼雷技术. 2009, 17(4): 20-24. Liu Wen-yuan, Zhang Jing-yuan, Lv Yang, et al. Scaling Target Echo Modeling Technology Based on Modified Highlight Model[J]. Torpedo Technology, 2009, 17(4): 20-24.

[7] 齐国清. 几种基于FFT的频率估计方法精度分析[J].振动工程学报. 2006, 19(1): 86-92. Qi Guo-qing. Accuracy Analysis and Comparison of Some FFT-based Frequency Estimators[J]. Journal of Vibration Engineering, 2006, 19(1): 86-92.

High Precision Frequency Estimation Method of Torpedo Acoustic Fuse Target Echo

XIESheng1,2, CHENHang1, YUPing2

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072 , China；2. 91388thUnit，The People′s Liberation Army of China，Zhanjiang 524022, China)

The estimation accuracy of Doppler frequency is affected by the body target effect in near field region of submarine and torpedo, therefore a fast and accurate frequency estimation method is presented in this paper to acquire Doppler frequency in submarine target echo. This method is a combined frequency estimation method based on Rife algorithm and Quinn algorithm, making full use of the low computational complexity of Rife algorithm and the good anti-noise performance of Quinn algorithm. Aiming at the problem that Rife algorithm and Quinn algorithm have larger frequency estimation error when signal frequency is close to the discrete frequency of the discrete Fourier transform (DFT), the modified items of the frequency from Rife algorithm and Quinn algorithm are weighed to improve the frequency estimation precision. The simulation result shows that the present method has stable frequency estimation performance with less computation, and its root mean square error (RMSE) approaches much closer to Cramer- Rao lower bound (CRLB) than the Rife and Quinn algorithms, which can well meet the requirement of torpedo acoustic fuse for predicting burst point accurately.

torpedo; acoustic fuse; frequency estimation; Rife algorithm; Quinn algorithm; Cramer-Rao lower bound; discrete Fourier transform (DFT)

TJ630.34; TJ431.7

A

1673-1948(2011)01-0014-06

2010-06-18;

2010-08-25.

武器装备预研基金资助项目(9140A05030409HK0337).

谢 胜(1976-), 男, 在读硕士, 主要研究方向为水下信号与信息处理.

(责任编辑: 杨力军)