含风电场的电力系统小干扰稳定性分析

刘小林 韩肖清 刘海龙 王鹏敏

（太原理工大学电气与动力工程学院，太原 030024）

1 引言

风力发电是新能源技术中最成熟、最具规模开发和商业化发展前景的发电方式之一，具有安全可靠，无污染，不需消耗燃料，建设周期短，规模大小灵活，可并网运行，还可以美化环境等显著优点，在能源、电力产业中异军突起。风能不但是一种洁净的自然能源，取之不尽，用之不竭，风力发电还没有其他发电方式所伴生的温室气体排放和环境污染问题，而且其蕴量巨大，全球的风能约为2.74×109MW，其中可利用的风能为2×107MW，比地球上可开发利用的水能总量还要大10倍。中国风能储量很大、分布面广，全国10m高度处风能储量为322.6×1010W，即32.26亿kW，这个储量是理论可开发量，当考虑风力机间的湍流影响及风力机叶片的实际扫掠面积等，中国风能实际可开发量为2.53亿kW[1]。

随着我国发电事业的不断发展，风电场的容量将会越来越大，而且随着电力系统的发展，将各个孤立的系统联合起来形成一个大的电力系统，也成为世界各国的普遍趋势，是电力行业向着高水平方向发展的客观要求。这种大型风电场并网运行将会对系统稳定性造成较大的影响。大区互联符合电网发展的一般规律，有利于大范围进行资源优化配置和提高运行经济性、可靠性（水火电互补、减少地区备用容量、错峰效应、事故情况下功率紧急支援等）。大区互联也符合我国能源、负荷的实际分布情况。对于电力系统，特别是区域互联的大电网电力系统，由于出现了与低频振荡相关的小干扰稳定性问题，而引起了人们对大区互联电力系统小干扰稳定性问题的关注[2]。因此，研究风电场接入电网后对电力系统安全稳定的影响有重要的理论意义和实用价值。

文献[3]讨论了风力发电系统建模的思想，对在国内外的风力发电机组建模中已经采用的模型、方法及其应用的优缺点进行了综合分析，并在分析的基础上，介绍了模型的简化方法和线性化方法，结合学科发展的趋势，提出了以后的发展目标，这对有关风力发电机组的建模和控制方面有一定的借鉴意义。文献[4]给出了风力发电机的数学模型及动态仿真曲线。它对风电场电力系统稳定性的研究及风水互补电力系统的研究提供了理论依据，有重要的现实意义。文献[5] 建立基于普通异步发电机的风电机组(异步风电机组)和电力系统模型，分析异步风电机组对电力系统小干扰稳定性及阻尼特性的影响。文献[6]为了研究风电场和电力系统相互作用的稳定性，提出一种用于小干扰稳定分析的风电系统的数学模型，并应用Matlab语言编程对新疆布尔津水电一风电系统进行了小干扰稳定分析。文献[7-9]研究了风电场接入系统后影响系统小干扰稳定性的因素。

本文在文献[3-6]的基础上建立了可用于小干扰稳定性研究的风力发电机组数学模型，在文献[7-9]的基础上通过算例研究含风电场的电力系统小干扰稳定性。

2 数学模型

2.1 风力机模型

风力机主要由叶片、轮毂、齿轮箱、联轴器等传动装置构成。

（1）叶片的主要作用是将风能转换成作用在轮毂上的机械转矩，此转矩与风速、空气密度、叶片半径等有关，关系如下：

其中，WT为风作用在叶片上产生的对转轴的机械力矩；WV 为风速，m/s；inV、outV 分别为风力机的切入和切出风速，m/s；ρ为空气密度；ω为风力机的机械角速度，rad/s；2S=πR为风力机叶片的扫略面积，2m，R为叶片半径，m；pC是风力机的风能利用系数， 根据贝茨理论，pC最大值为0.593。

（2）轮毂的作用是用于连接叶片和齿轮箱，具有较大惯性，其输入和输出转矩可用一阶惯性环节表示：

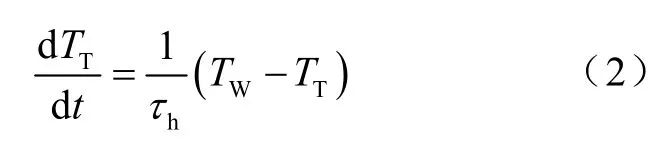
式中，TT为齿轮箱输入侧的转矩，hτ为轮毂的惯性时间常数。

（3）齿轮箱和联轴器为传动装置，传递风轮机和发电机之间的转矩，其动态方程如下：

式中，ω为风轮机转速，mT为齿轮箱输出侧的转矩，ττ为齿轮箱的惯性时间常数。当风力发电机运行于 稳定状态时，转速基本保持不变，即，此时，可近似认为mT与TT相等。

2.2 桨距角控制系统模型

风能利用系数 pC是叶尖速比λ和桨距角β的函数。当风速变化时，风力机运行点将发生变化，为了保证风能的利用效率，并且使风轮机输出平稳，需要对桨距进行调整。通常用下式表达：

式中，β为桨距角；βτ为桨距控制系统的惯性时间常数。

2.3 异步发电机模型

小干扰稳定性分析中，忽略定子磁通暂态过程，而只考虑转子绕组暂态（以下是按电动机惯例的暂态模型）。

（1）定子电压方程

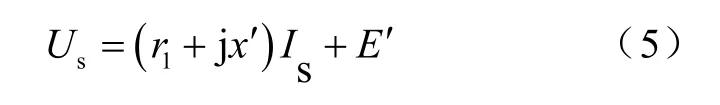
（2）电磁暂态方程式

式中，sU、sI、E′分别为发电机定子电压、定子电流和暂态电势；， 为定子开路时间常数；1r、2r、1x、2x、mx、f0分别为异步发电机定子电阻、转子电阻、定子电抗、转子电抗和激磁电抗标幺值、系统频率基值。

（3）转子运动方程式

从以上分析可知，风力发电机的数学模型是一组非线性方程。研究其小干扰稳定性时需对其在稳定点进行线性化，得到状态方程。然后通过求状态矩阵的特征值，得到系统的小干扰稳定性。非线性方程线性化结果如下：

式中

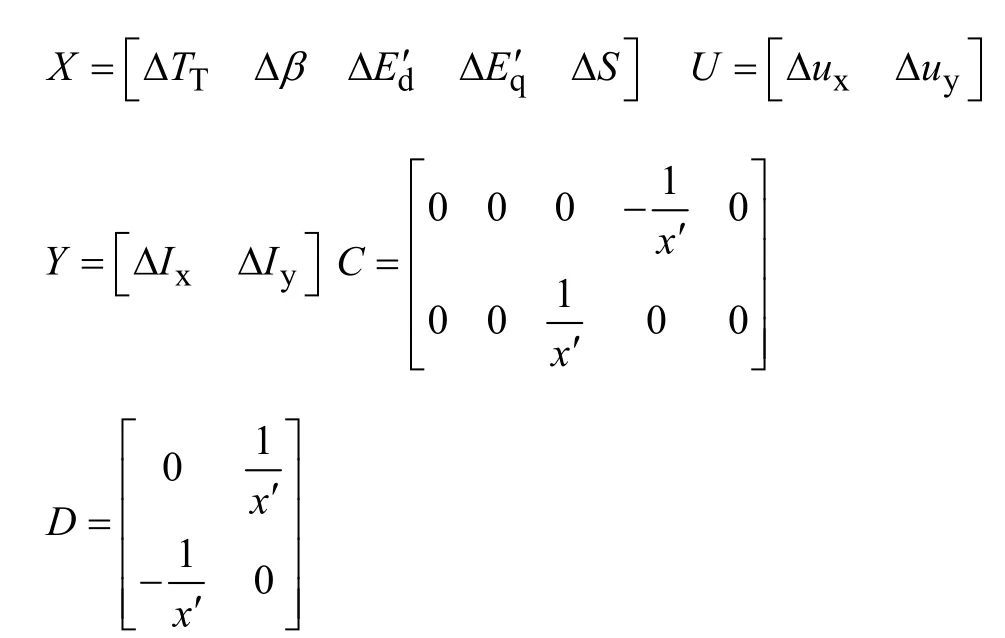
注：设定异步发电机的dq轴与同步坐标XY轴重合。

3 算例分析

3.1 简单系统分析

异步风电机组与无穷大电力系统构成的简单风力发电系统包括普通感应异步发电机、升压变、无穷大母线、无功补偿装置，系统的接线如图1。算例采用标幺值计算。

图1 简单系统

异步发电机的参数如表1。

表1 异步发电机参数（以额定容量为基准值）

每台异步发电机的电容补偿参数：

（1）电容补偿参数变化时的计算结果

风力发电机接入系统时，其出口端通常要安装无功补偿电容来提供异步风力发电机的无功需求。本文通过改变容抗的大小来研究其对系统小干扰稳定性，表2是容抗变化时系统特征值变化的情况。由表2可知，风电机系统在小扰动下具有良好的稳定性，与异步发电机滑差和发电机暂态电势的q轴分量强相关的振荡模态（λ）的阻尼较好，其阻尼比在0.25～0.27之间。随着容抗的增大，其振荡频率和阻尼比变化不大。

表2 风电场电容补偿参数变化时系统的特征值变化（风力机的出力 P= 1.0，功率因数cosφ = 0.99， xl= 0.042）

在风力机有功率和功率因数以及线路长度不变的情况下，随着容抗的增大即功补偿容量的减小，导致风电机机端电压下降。

（2）改变风电场出力时的计算结果

通过增加风电机的台数，即风电机的出力来研究简单系统，研究过程中将多台相同的发电机折合成一台等值机；然后用研究单机的方法来分析多机风电场的小干扰稳定性。表3是改变风电机的台数时系统特征值变化情况。由表3可知，多机风电场系统在小扰动下具有良好的稳定性，与异步机的滑差率（s）和暂态电势的q轴分量（ qE）强相关的振荡模态（λ）的阻尼较好，阻尼比在0.25～0.27之间。随着风电场出力增加，其振荡频率和阻尼比变化不大。

表3 风电场出力变化时系统的特征值变化 （ xl= 0.01，功率因数cosφ = 0.98）

在风力机有功率和功率因数以及线路长度不变的情况下，随着风电机台数的增加，导致风电机机端电压下降。

3.2 风力场接入多机系统

风电场通过变压器和线路接于图2系统上（图2是在IEEE四机两区域系统上增加一个区域3，区域3中的发电机G5、G6分别与区域2中G3和G4相类似），区域1经区域3流向区域2的功率为400MW。

系统基准容量值：100MVA，系统具体数据参看文献[10]。异步感应发电机的参数同上例，每台异步机的功率为0.03-j0.0142。六机系统的出力和负荷如附表8。

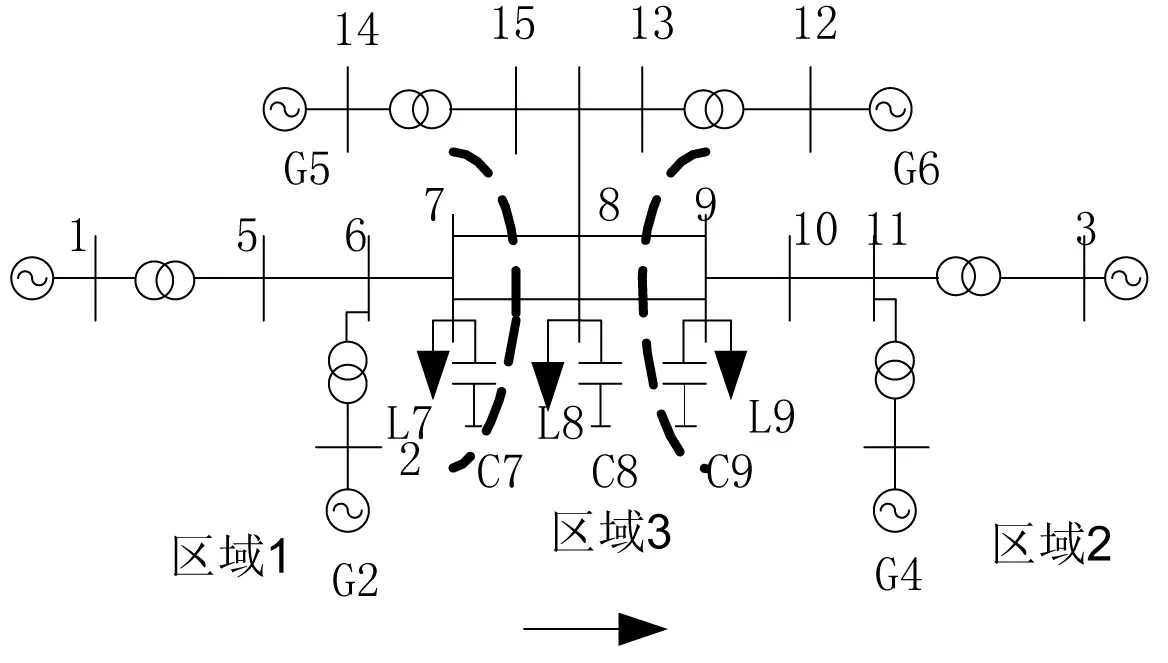
图2 风电场接入六机系统

（1）方案一

风力发电机接入区域1的节点6；改变风电场的出力，为了保持系统的负荷平衡，通改变本区域内的同步发电机的出力来维持系统功率平衡，导致区域内的常规发电机组运行方式发生变化，从而会影响系统振荡模式和振荡特性的变化，计算表明与风力发电机强相关的振荡模式和局部振荡模式有较好的阻尼特性，因而不是本文的研究重点，以下重点是研究阻尼比很低的两种区域间振荡模式的阻尼特性。

从表4-表5可以看出随着风电场出力的增大，区域间的振荡模态1和振荡模态2的阻尼比都有所增加。随着风电场出力的增加（直到常规发电机G2被取代），使得区域之间振荡模式的阻尼阻尼比增大。阻尼比的增大是由于系统运行方式发生变化，因为发电机G2出力逐渐减小直到停机。

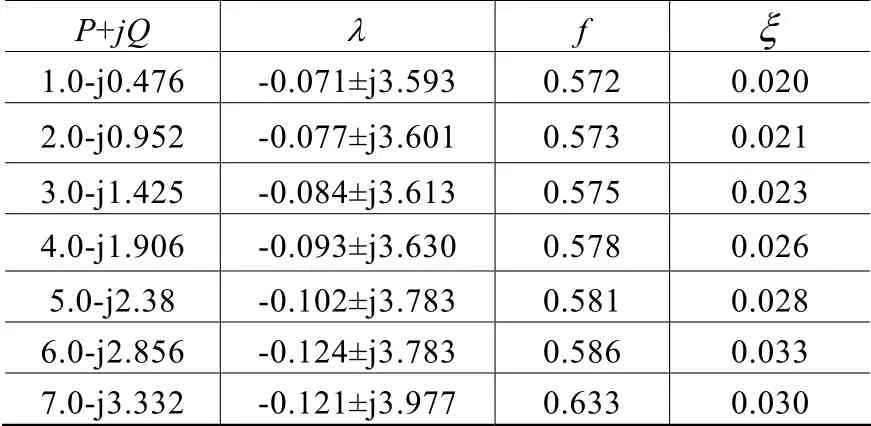
表4 振荡模式1

表5 振荡模式2

（2）方案二

风电场接入区域2的节点10；改变风电场的出力，通过减小区域3的同步发电机的出力来维持系统功率平衡。表5-表6是风电场出力变化时，区域间振荡模式的振荡特性的变化情况。从表5和表6可以看出随着风电场出力的增大（直到常规发电机G5被取代），区域间振荡模态1的阻尼比有所减小而区域间振荡模态2的阻尼比明显增大。阻尼比的变化是由于系统的运行方式发生了变化，因为发电机G5出力逐渐减小直到停机。

表6 振荡模式1

表7 振荡模式2

4 结论

本文通过算例分析，可以得到以下结论：

（1）风电机组接入无穷大系统时，与异步机的转差率和暂态电势的q轴分量强相关的振荡模态有着较好的阻尼比，随着机端无功补偿容抗值和风电机组出力变化时，其振荡频率和阻尼比都变化不大，即风电机系统在小扰动下具有良好的稳定性。

（2）风电场接入多机系统的区域1的节点6，改变风电场的出力，通过改变本区域内的同步发电机的出力来维持系统负荷平衡，随着风电场出力的增大（直到常规发电机G2被取代），区域间振荡模态1和振荡模态2的阻尼比都有所增加，有利于其小干扰稳定性。

（3）风电场接入多机系统的区域2的节点10；改变风电场的出力，通过减小区域3的同步发电机的出力来维持系统负荷平衡。随着风电场出力的增大（直到常规发电机G5被取代），区域间振荡模态1的阻尼比减小，更容易发生振荡，而振荡模态2的阻尼比增大，有利于其小干扰稳定性。

表8

[1] 王承煦,张源.风力发电[M].北京：中国电力出版社,2003.

[2] 关宏亮,杨以涵,戴慧珠.大规模风电场接入电力系统的小干扰稳定性研究[D].保定：华北电力大学,2008.

[3] 董萍,吴捷,杨金明,陈渊睿.风力发电机组建模研究现状[J].太阳能学报,2004,25(5).

[4] 侯书红,蔺红,晁勤.祖拉提风力发电机的建模及动态仿真[J].新疆工学院学报,2000,21(3).

[5] 关宏亮,迟永宁,戴慧珠,杨以涵.异步风电机组接入系统的小干扰稳定及控制[J].电力系统自动化,2008,32 (4).

[6] 樊艳芳,晁勤.水电风电系统的小干稳定性分析[J].水力发电,2008,5(34)：97-99.

[7] 包含风电场电力系统的小干扰稳定性分析建模和仿真[J].电网技术,2004,28(1).

[8] Mendonca.A,Lopes.J.A.P.Impact of large scale wind power integration on small signal stabbility,IEEE,CONFERNCES 2005,5pp.-5

[9] Gautam,D.,Vittal,V.,Harbour,T.,Impact of Increased Penetration of DFIG-Based Wind Turbine Generators on Transient and Small Signal Stability of Power Systems,IEEETrans.2009,24(3)：1426-1434.

[10] (加)昆德(Prabha Kundur)著；电力系统的稳定与控制[M].《电力系统稳定与控制》翻译组译．北京：中国电力出版社,2001.