改进型谐波电流检测的仿真研究

栗文义 王 妍 王川宇

（1.内蒙古工业大学电力学院，呼和浩特 010080； 2.中科院建筑设计研究院有限公司，北京 100190）

1 引言

有源电力滤波器（APF）是一种向电网注入与电网谐波电流大小相等方向相反的谐波电流，从而实现滤波的装置。为了提高有源电力滤波器的工作性能，对电网谐波电流的快速、准确检测非常重要[1]。

目前，国内外应用于APF的谐波电流检测方法主要有傅里叶变换法、基于瞬时无功功率理论的pq变换法和ip-iq变换法。傅里叶变换法基于对周期数据的分析，计算量大，不适宜于快速实时控制[2]；pq变换法和ip-iq变换法能从电流瞬时值中直接分离出谐波分量，但pq变换法和ip-iq变换法都是基于瞬时无功功率理论提出的，其变换过程中的三相到两相及其反变换都是为了求得无功功率值，这在谐波检测中并不需要[3]。传统的pq变换法和ip-iq变换法都需要锁相环（PLL）获取同步旋转角，不可避免地带来延时误差[4]；为了克服这个问题，本文根据基于基波幅值分离法检测谐波电流的方法，论证了略去该系统中的锁相环的可能性。

2 基于基波幅值分离法的谐波检测方法

2.1 基本理论

基于三相电路瞬时无功功率的ip-iq检测算法，其实质是把待测的三相瞬时电流、电压，经线性变换后相乘，从而使得基波电流所对应的瞬时功率为一直流量，以便于分离出去[3]。若电压畸变时，则通过一个锁相环产生与电压同相的正弦信号，代替电压信号，从而准确地测出谐波电流。因此，基于基波幅值分离的瞬时谐波电流实时检测算法的主要特点是对畸变电流中的基波成分和无功电流成分的幅值分别进行计算，然后通过低通滤波器把它们分离出来，最后得到基波有功和无功电流分量。所以称这种谐波检测方法为基波幅值分离法(Fundamental Amplitude Separate)[5]。

设电源电压是一个纯正弦波形，表示为

其中，smu 是电源电压的振幅，f是电源频率，f=50Hz；电网瞬时电流si表示为

基波电流1i分解成两项，即

将式（3）带入式（2）得

其中，1i为基波电流，pi为瞬时有功电流，qi为瞬时无功电流，hi为谐波分量。

2.2 略去锁相环的方法实现与证明

基于瞬时无功功率理论的三相谐波电流检测方法通过正弦信号sinωt和余弦信号cosωt把经过派克坐标变换后的畸变电流分解为直流分量和交流分量，然后再用低通滤波器把它们分离。受此启发，对畸变电流的运算如下[6]。

将式（4）两端分别乘2sinωt，根据三角函数的有关特性得

显然式（5）实际上是由直流分量和交流分量两部分组成，而直流分量正是pI。通过一个低通滤波器（LPF）把它分离出来，与sinωt相乘，得到pi。

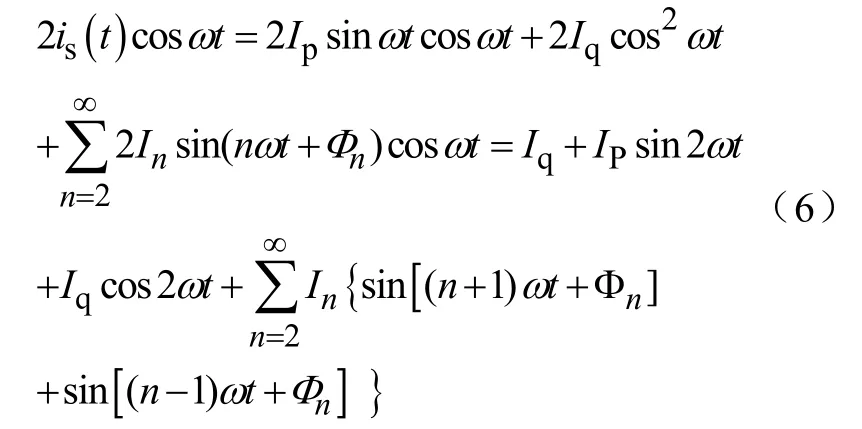
式（6）含有的频率成分与式（5）一样，也是由直流分量和交流分量两部分组成，而直流分量正是qI。通过LPF也能把它分离出来，与 tωcos 相乘，得到的就是pi。在得到pi和qi后，代入式（3）就能得到1i。从式（2）可得到hi，从式（4）即可获得q hi i+等电流分量。

下面以单相电路为例来分析基波幅值分离法的特性。框图如图1所示。

图1 基波幅值分离法原理图

图中Us为电源相电压，通过正弦信号发生电路得到sinωt。PLL为锁相环，它的作用是锁定电压信号，让正弦波发生器产生一个与电网电压同频同相的正弦波。LPF为一低通滤波器，用来滤掉基波以外的其他高次谐波。如果电源电压有畸变，那么它将包含除基波分量之外的其他谐波分量。此时通过PLL及正弦、余弦信号发生电路得到的正弦、余弦信号。由Us的基波分量可知，pi与Us的基波分量同相，而qi与Us的基波分量正交[4]。因此，式（5）和式（6）的计算过程不变，所以Us畸变不会影响到检测的结果。假如电源频率发生了漂移，由于正弦、余弦信号和si中的1i及各次谐波的频率也会同步发生变化，式（5）和（6）的计算过程是一样的，从而不会影响图1电路的性能。研究表明，当进行谐波电流检测时，可以不必跟踪电源电压基波分量的相位，也就是说，图1中的锁相环可以省去，而只需通过控制电路产生与电源电压同频率的正弦、余弦信号，而相位可以任意。

由上述理论可证明，相位差θ并不影响瞬时基波电流的检测，即对谐波电流的检测没有影响，在应用时，可以略去锁相环，而通过控制电路产生与电网电压同频率的正弦、余弦信号参与计算，这样实现起来更加简单。这种单相电路的谐波检测方法，其电路结构简单、动态响应速度快、检测精度高，是一种便于实现的实时检测方法。实际应用时它既可以单独检测出谐波电流，又能得到谐波和无功电流之和。这种方法经适当变形，也可应用于三相电路的谐波电流的检测[4,5,7]。

2.3 仿真分析

（1）电流信号为负载输出的谐波信号。系统中低通滤波器采用二阶Butterworth，截止频率选取为f=20Hz。系统中控制电路所产生的正弦、余弦信号分别为sinωt、cosωt。

系统仿真模型如图2。

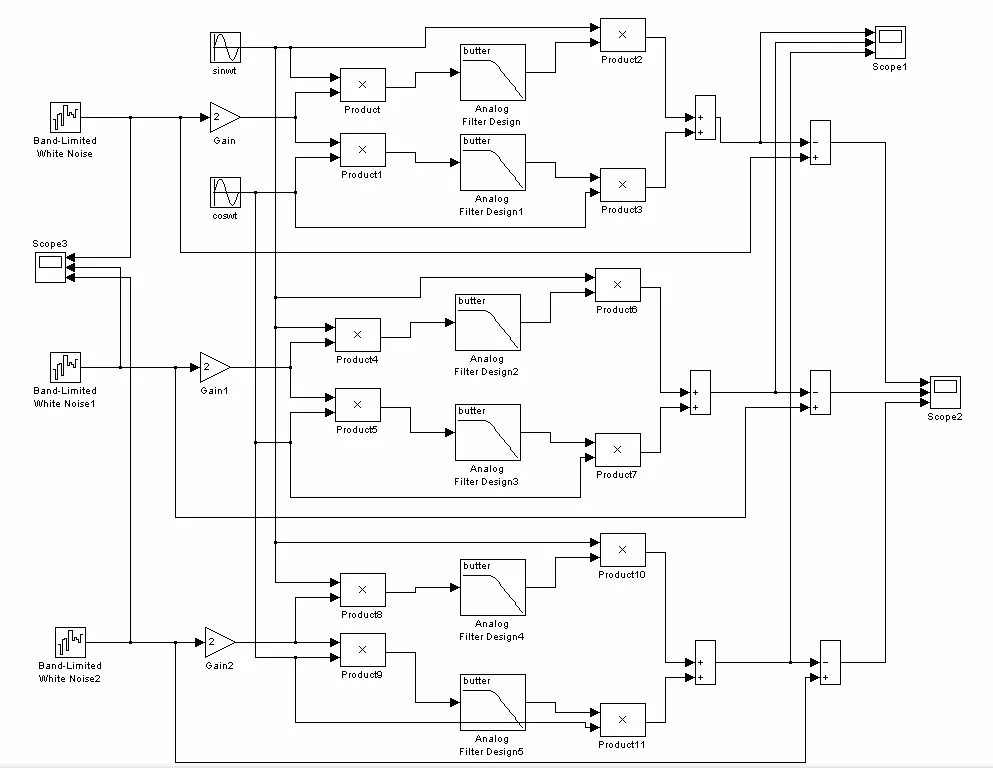
图2 三相电路谐波电流检测的基波 幅值分离法的仿真模型

图3 三相电路谐波电流检测的基波 幅值分离法的仿真波形

（2）电流信号为负载输出的谐波信号。低通滤波器采用二阶Butterworth，截止频率选取为f=20Hz。系统中控制电路所产生的正弦、余弦信号分别为

系统仿真模型如下图4。

图4 三相电路谐波电流检测的基波幅值分离法 （有相位差）的仿真模型

图5 三相电路谐波电流检测的基波幅值分离法 （有相位差）的仿真波形

仿真实验表明，图（5）的仿真波形同图（3）的仿真波形完全一致，因此充分印证了相位差θ并不影响瞬时基波电流的检测。即对谐波电流的检测没有影响。因此在设计电流检测系统时，可以略去锁相环。

3 结论

经过计算与仿真验证了相位差θ并不影响瞬时基波电流的检测，即对谐波电流的检测没有影响。也就是说，当进行谐波电流检测时，可以不必跟踪电源电压基波分量的相位，锁相环可以省去。仿真结果表明，基于基波幅值分离法的仿真方法结构简单，适时性好，不仅适用于三相电路，也适用于单相电路。

[1] 李欣媛.并联型有源电力滤波器的仿真及软件设计[D].北京交通大学,2009.

[2] 李圣清,朱英浩,周有庆．电网谐波检测方法的综述[J].高电压技术,2004,33(3)：39-42.

[3] 王丽,刘会金,王陈．瞬时无功功率理沦的研究综述[J].高电压技术,2006,32(2)：98-101．

[4] 周林,甘元兴,雷鹏等．基于瞬时无功功率理论的谐波检测新方法[J].高电压技术,2005,31(10)：67-70.

[5] 蒋斌,颜钢锋,赵光宙.单相电路瞬时谐波及无功电流实时检测新方法[J].电力系统自动化,2000,24(21)：35-38.

[6] 耿云玲,王群.单相电路的一种谐波和无功电流实时检测方法[J].国防科技大学学报,2000,22(4)：111-115.

[7] 杨君,王兆安.三相电路谐波电流两种检测方法的对比研究[J].电工技术学报,1999(2)：14-17.

[8] 王兆安,杨君等.谐波抑制和无功功率补偿[M].北京：机械工业出版社,2004,70-90.

[9] 公茂忠,刘汉奎,顾建军.并联型有源电力滤波器参考电流获取的新方法[J].中国电机工程学报,2002,22(9)：43-47.

[10] 马宝娟.基于谐波电流快速检测方法的并联型有源电力滤波器设计[D].哈尔滨理工大学,2007.