工序能力指数标准化定义之应用(双侧限)

于善奇 安 军

工序能力指数标准化定义之应用(双侧限)

于善奇 安 军

在双侧规范的情形下,研究了工序能力指数标准化定义的依据;在以不合格品率(p)为质量指标的情形下,不仅证明了p与CP、ε(偏移量)之间的计算公式,而且给出详尽的数值表。此外,还给出了典型的应用示例,供企业参照。

双侧限 工序能力指数 标准化 数值表

1 双侧限工序能力指数标准化定义的依据

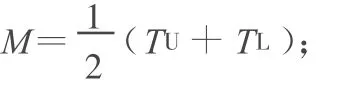
加工过程的偏移量ε=|μ-M|。

1.1 工序无偏的情形

当工序无偏时,即偏移量 ε=|μ-M|=0,双侧限工序能力指数的标准化定义[1]为

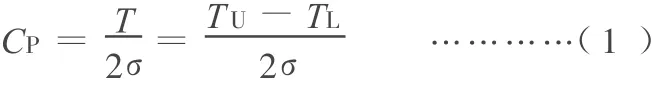
由于TU-M=M-TL,注意到 ε=0,即 μ=M时,TU-TL可改写为

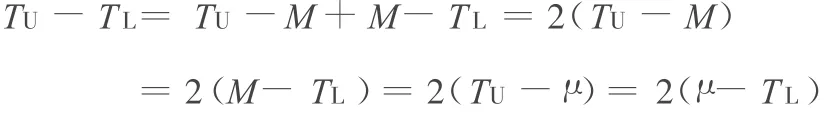
于是,式(1)可改写为

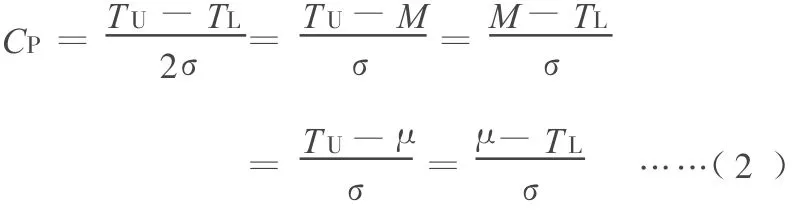
当工序有偏时,偏移量 ε=|μ-M|≠0,双侧限工序能力指数的标准化定义为

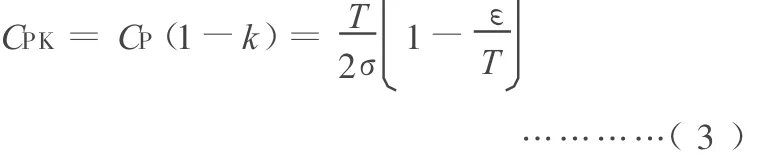
2 在双侧限工序能力指数的标准化定义下,产品质量的分析

2.1 工序无偏的情形

在工序无偏的情形下,注意到式(2),加工过程的不合格品率p与CP间的关系为

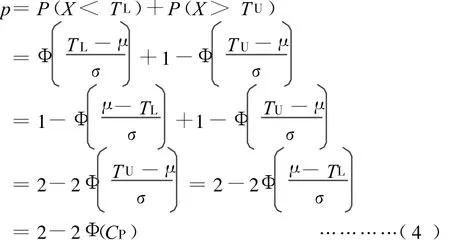
2.2 工序有偏的情形

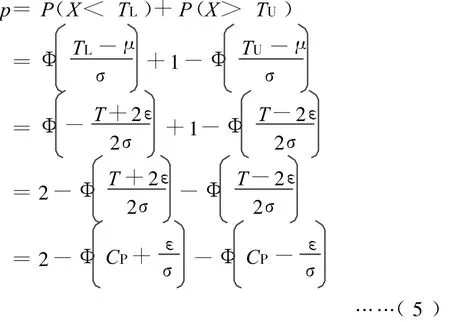
根据式(5),若给定偏移量ε=a·a(这里的系数a为实数,比如 α=1.5,表示偏移 1.5σ),不难得出p与CP间的数值表。显而易见,当 ε=0时,式(4)是式(5)的特例。限于版面,本文仅给出CP值和偏移量ε的常用变化范围,其中CP的步长为0.1,ε的步长为0.05σ,参见表1。必须指出,有的企业不是根据实际偏移状态,一律按偏移1.5σ分析产品质量,是不妥当的。此外,对某一特定企业而言,根据CP值的特定变化范围和偏移量的大小,可以利用式(5)将数值表细化。

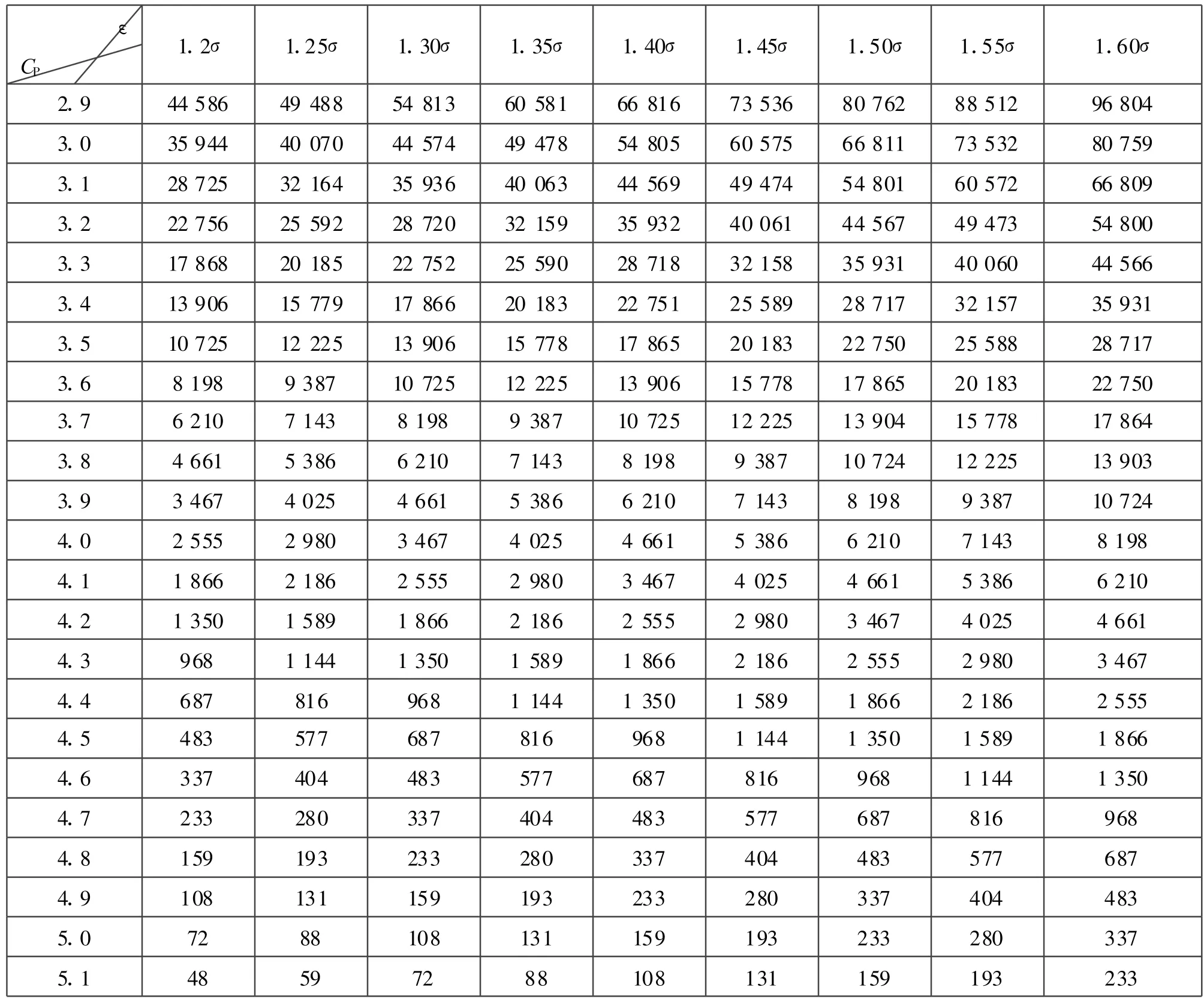
表1 不合格品率 p与CP、ε间数值表(双侧限)

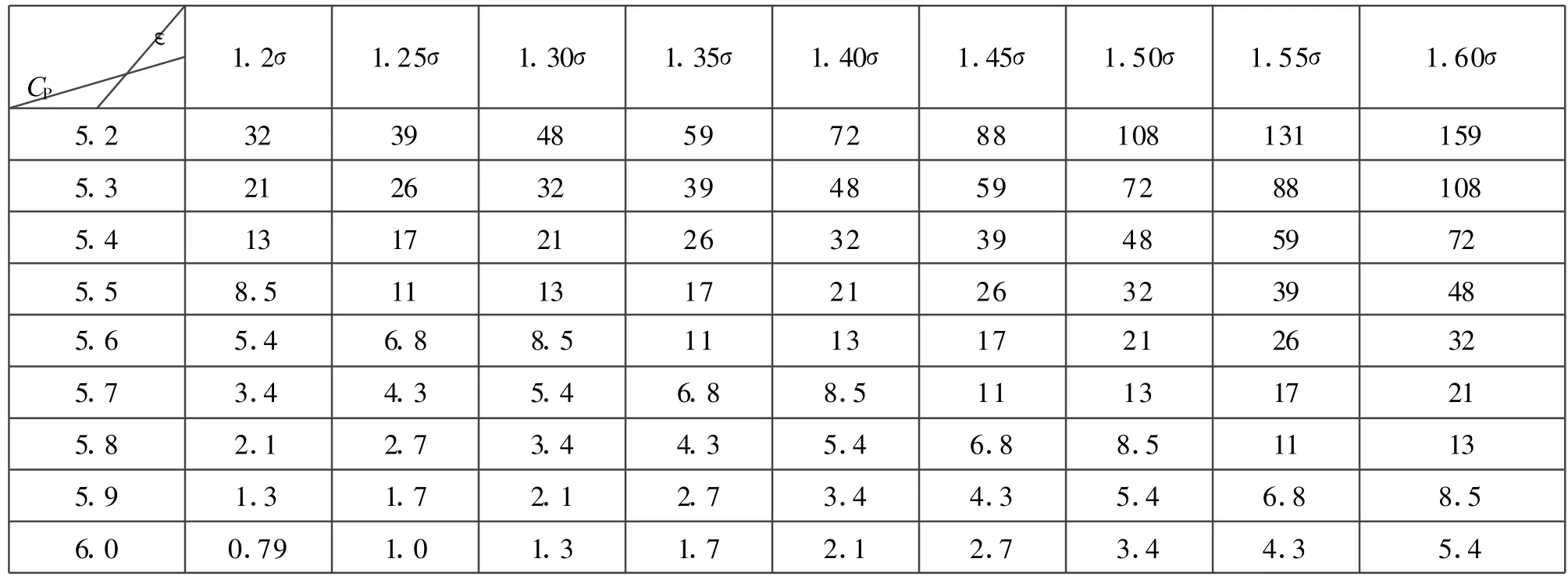
续表1

2.3 应用示例

例1.某产品某项特性的规范上限TU=5.02(mm),规范下限TL=4.98(mm),规范中心M=5.00(mm)。已知加工过程稳定,该工序长期统计结果表明,均值 μ=5.008(mm),标准差 σ=0.0051(mm)。试确定该工序的CP值和加工过程的不合格品率。

解： 先求标准化定义的CP值。这是双侧限的情形,已知标准差σ=0.0051,公差T=TU-TL=0.04,所以

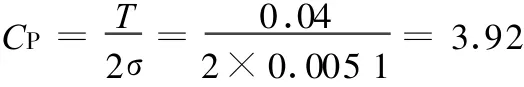
由于偏移量 ε=|μ-M|=0.008,σ=0.0051,所以 ε=1.57σ。具备一定基础的读者,不难依据式(5)计算得到

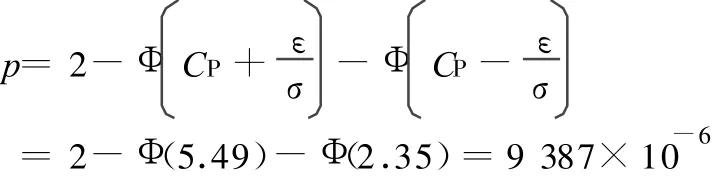
不具备一定基础的读者,可以查表1得出近似结果。

例2.采用某种设备灌注瓶装酒,标准规定每瓶酒净重(500±2)mL,平均净重M=500(mL)。某天上午10点随机抽测8瓶酒,测得样本均值¯x=500.5(mL),样本标准差S=0.482(mL)。试分析该工序的CP值和瓶装酒的不合格品率。

解： 先求标准化定义的CP值。由于样本量n=8,样本标准差S=0.482,所以标准差 σ的无偏估计值为

其中C4称为修偏系数,其值参见表2[2]。已知产品公差T=4,于是CP值为

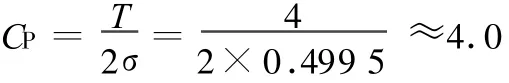
又偏移量ε=|μ-M|≈0.5,≈0.4995,故ε≈1.0,查表1可知,当CP=4.0,ε=1.0σ时,瓶装酒的不合格品率p=1350×10-6。

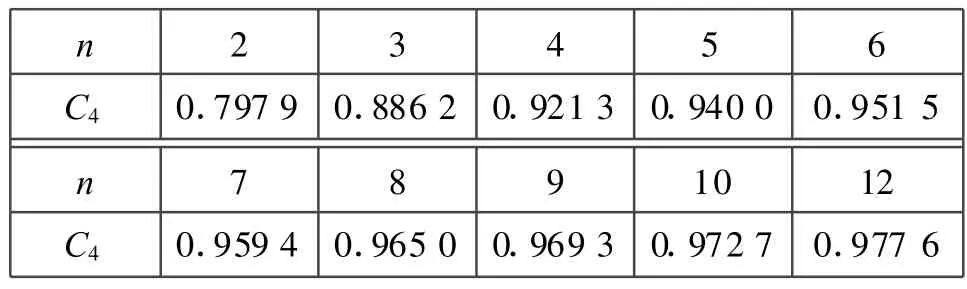
表2 正态分布标准差的修偏系数C4

3 在双侧限工序能力指数的标准化定义下,CP值的评级参考

在双侧限工序能力指数的标准化定义下,CP值的评级参考见表3。

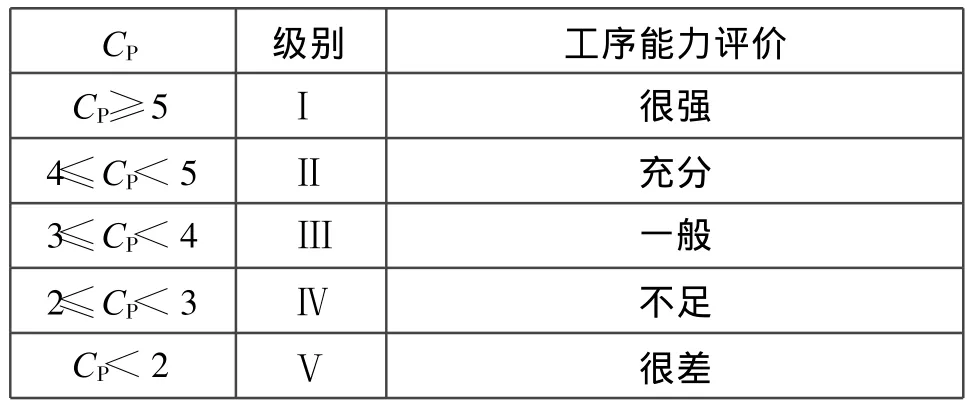
表 3 CP值的评级参考(双侧限)

需要指出,表3中CP值的评价仅是笼统性提法。CP值的大小取决于SMIE,其中最主要的因素是加工设备的精度和原材料的质量水平,其次是操作者的技术水平及工艺方法等因素的影响,这些因素可归纳为技术与管理两大类。比如,对Ⅱ级加工的评价是技术与管理能力都很好,应继续维持;对Ⅲ级加工的评价是技术与管理能力一般,不是很好,应设法提高到Ⅱ级。一般说来,Ⅰ级加工适用于电子行业;Ⅱ级加工适用于机械行业;Ⅲ级加工适用于化工类行业。

[1]于善奇.工序能力指数全新定义的探讨[J].标准科学,2009(2)：9-10.

[2]于善奇.质量专业常用统计技术[M].华龄出版社,2003：70-71.