应用组合预测法对我国月度PPI的预测评价
杜淑女,王斌会
(暨南大学 统计系,广州 510632)
0 引言
PPI是衡量工业企业产品出厂价格变动趋势和变动程度的指数,是反映某一时期生产领域价格变动情况的重要经济指标,也是制定有关经济政策和国民经济核算的重要依据,而经济指标的准确预测是国家对宏观经济正确调控的必要前提,但经济系统是一个非常复杂的系统。因此要准确地预测某一趋势,必须从多个方面进行考虑。每种预测各有其特点,在不同的方面有各自的优劣,因此为了准确地预测结果,可考虑采用组合预测法进行预测。对于同一预测问题而言,由于考虑的角度、方式和层次等不同,可为其提供不同的预测方法,将这些方法进行组合,可增大信息量,能够更好地进行预测。组合预测将各种预测效果进行综合考虑,比单个预测模型更系统、更全面。而且,Bates和 Granger证明了两种或两种以上无偏的单项预测可以组合出优于每个单项的预测结果,即能够有效地提高预测的精度。为了有效地利用各种模型的信息,提高模型的预测精度与模拟评价效果,有必要对PPI进行组合预测。组合预测方法是建立在最大的利用信息的基础上,它通过组合多个单项预测模型,集结这些模型中所包含的信息,因此,在大多数情况下,通过组合模型进行预测,更全面、更可靠,可以达到改善预测结果的目的。
基于组合预测模型的优越性和自回归移动平均模型的建模机理,本文将以 2001年 1月至2010年 7月的月度定基 PPI数据为对象,建立了三个单项 ARIMA模型,为了有效地利用各种模型的信息,提高模型的预测精度与模拟评价效果,本文依据组合预测的原理将这三个单项预测模型进行组合,通过实例分析和精度检验。
1 组合预测理论
组合预测法是指通过建立一个组合预测模型,把多种预测方法所得到的预测结果进行综合,以得到一个较窄的预测取值范围供系统分析和决策使用。由于组合预测模型能够较大限度地利用各种预测样本信息,比单项预测模型考虑问题更系统、更全面,因而能够有效地减少单个预测模型受随机因素的影响,从而提高预测的精度和稳定性,下面分别具体介绍几种组合预测法。
1.1 最优加权法
现在运用最广泛的组合预测法是最优组合预测法,最优组合预测就是对单一预测方法进行组合得到最优权数,也叫最优加权法。最优加权法的基本原理是依据某种最优准则构造目标函数Q,本文中目标函数为残差平方和即Q=eTe,在约束条件下运用最小二乘法极小化 Q求得综合模型的加权系数。
1.2 正权综合法
最小二乘准则下的最优权重可能出现负值,这与实际往往不相符合。所以在约束条件中增加正权重约束以得到次优的权重组合。常用的正权组合类型有算术平均法、方差倒数法和均方倒数法。
(1)算术平均法也可称为等权平均法,即对各模型赋予相同的权重。该法计算简单,应用较为普遍。
(2)方差倒数法的权重是单个模型的方差倒数与所有模型的方差倒数和的比例。
(3)均方倒数法的权重是单个模型的方差倒数的均方与所有模型的方差倒数的均方和的比例。
1.3 AFTER算法
2001年爱荷华州州立大学的Yuhong Yang提出了一种新的组合预测方法,即AFTER算法 (Aggregated Forecast Through Exponential Reweighting),这种算法计算权重只依赖于过去的预测值和观测值,因此被称为AFTER算法。令Y1,Y2,…,Yn为观察序列,权重为 Wj,n,当 n=1 时,Wj,1=1/J ;当n≥2时,权重为:

其中:

2 我国月度PPI时间序列分析建模
2.1 数据来源
通过查阅 2001~2010年的《中国统计年鉴》,得到了我国 2001年 1月~2010年7月的工业品出厂价格指数,具体的数据如表1所示。
2.2 单项预测法方法

表1 工业品出厂价格指数

表2 ARIMA(2,1,4)模型系数

表3 ARIMA(5,1,1)模型系数

表4 ARIMA(2,1,7)模型系数
对以上数据建立单项预测模型,即自回归移动平均模型ARIMA(p,d,q),通过比较每次模拟模型的 AIC值,我们选取AIC值最小的三个模型,分别为 ARIMA(2,1,4)、ARIMA(5,1,1)以及 ARIMA(2,1,7),运用 R软件估计自回归移动平均模型,得到模型的系数如表2、表3、表4所示。
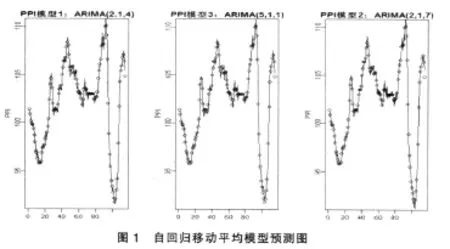
图1描述的是工业品出厂价格指数自回归移动平均模型 ARIMA(2,1,4)、ARIMA(5,1,1)以及 ARIMA(2,1,7)的 预 测图,其中点代表的是实际的观测值,而实线是自回归移动平均模型的预测值,从预测图上可以看出这三个单项自回归模型预测的结果还不错,大部分的预测实线都穿过了实际观测值,但是还有有一部分实线段明显超出了实际观测值的范围。通常单项预测方法会忽略某一方面因素或是对某种预测的不适应,从而导致单项预测的精度大大下降。如果进行组合预测的话,则可以通过增加模型的个数并且把各个模型加权组合起来,从而达到提高组合预测精度的目的,一般单项预测模型的精度越高其组合预测的精度也越高。
2.3 组合预测法方法
为了提高以上建立的单项预测模型的精度,针对以上建立的三个自回归移动平均模型建立组合预测模型。本文中我们分别采用算术平均法、方差倒数法、最优加权法和 AFTER法建立组合预测模型,运用 R软件计算各种方法预测模型的权重:由于算术平均法对每个模型赋予相同的权重,因此有w1=w2=w3=1/3。利用模型估计得到的残差就可以算出方差倒数法的权重,方差倒数法的权重分别为w1=0.3068002,w2=0.3663674,w3=0.3268324。一旦残差算出来了,我们就可以根据残差阵算出最优加权法的权重,分别为w1=-0.4091075,w2=0.9448174,w3=0.4642901。计算 AFTER算法的权重只需知道以上单项模型估计得到的残差就可,那么从AFTER算法的计算公式中看出它是对每个模型的每一个观测值赋予一个权重,因此一共有345个权重。
图2描述的是组合预测模型的预测图,其中点代表的是实际的观测值,而实线是组合预测模型的预测值,和单项自回归移动平均模型预测图相比较组合预测模型预测的更好一些,组合预测模型预测图中实线几乎和所有的点重合了,而单项预测模型预测图中存在一部分线段超出了实际观测值的界限。因此组合预测法的拟合精度明显高于单项预测法的拟合精度。

3 组合预测法的评价
为了更好地评价组合预测法,必须制定一套切实可行的指标来检验组合预测效果的好坏,对组合预测效果进行全方位的综合性衡量和评价。按照预测效果评价原则和惯例,本文提供以下评价指标作为参考,其中 Yt是实际观测值,Y^t是预测值;n为实际观测值个数。
(1)均方误差(MSE):均方误差就是各测量值误差的平方和的平均值的平方根。
(2)平均相对误差(MPE):它度量的是相对误差的平均值,而相对误差是绝对误差与测量值或多次测量的平均值的比值。
(3)Theil不等系数(U):Theil不等系数衡量预测模型预测能力指标,0≤U≤1,当U→0时说明预测精确度高,U→1时说明预测的精确度较低.Theil不等系数计算公式如下:
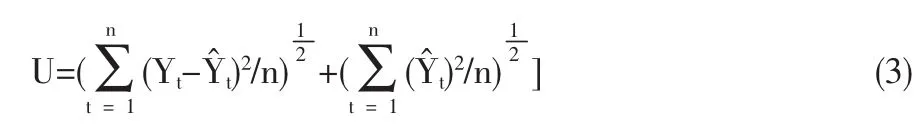
(4)净均方预测误差ANMSEP(net mean square prediction error):下的条件均值,净均方预测误差值越小说明模型预测的越好。四种组合模型预测结果的精度如表5所示。
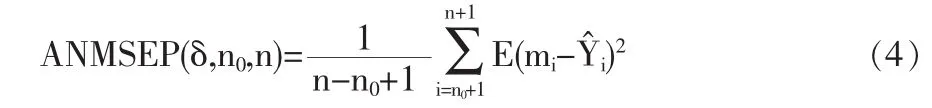
对比一下在这四种组合预测模型的预测评价指标,最优加权法的组合预测模型的均方误差、平均相对误差、Theil不等系数以及净均方预测误差的取值都是最小的,从这个角度
其中mi为 Yi在先前观测值可以看出最优加权法的组合预测模型拟合效果不错;其次AFTER算法的预测评价指标值都小于算术平均法和方差倒数法的预测评价指标,说明 AFTER算法的组合预测模型优于算术平均法和方差倒数法的组合预测模型。尽管最优加权法的预测评价指标值都是最优的,但是前面我们算出最优加权法的权重 w1=-0.4091075为负数,显然这是没有实际的经济意义,因此综合评价预测指标我们得出 AFTER算法的组合预测模型是最优的。

表5 组合模型预测精度表
运用 AFTER算法进行组合预测得到的预测值的预测误差均低于 2.52%,远远小于 10%,因此用 AFTER算法进行组合预测是科学的。最后运用 AFTER算法对我国 2010年月度 PPI进行外推预测,预测得到 2010年 8月的 PPI为 103.82118,最近国家统计局公布出 2010年 8月份的PPI为 104.1,预测误差仅为 0.45%。这进一步证明了用AFTER方法进行组合预测是科学的。
4 结论
PPI是我国物价测度指标体系的核心组成部分,是判断宏观经济走势的重要经济指标,它能够灵敏的反映社会供求变化。本文基于我国 2001年 1月~2010年 7月的月度PPI数据建立 ARIMA模型进行单项预测,然而采用单项预测模型难以做到充分利用已有的信息资源,预测能力欠缺。为了充分利用信息、全面提高预测精度,本文运用算术平均法、方差倒数法、最优加权法以及 AFTER算法这四种组合预测法对我国月度 PPI进行组合预测,并且运用均方误差、平均相对误差、Theil不等系数以及净均方预测误差这四个预测效果评价指标来比较四种组合预测法的预测精度,最后得出 AFTER算法是最佳的。运用该方法进行外推预测,预测结果显示 2010年 8月份的 PPI预测误差仅为 0.45%,表明该方法是科学的。
[1]PPI,百度百科[EB/OL].http://baike.baidu.com/view/101651.htm.
[2]唐小我.最优组合预测的计算方法[J].管理现代化,1992,(1).
[3]李学全.最优组合预测非负权系数的计算方法研究[J].预测,1995,60(4).
[4]Zhuo Chen,Yuhong Yang.Time Series Models for Fore Casting:Testing or Combining?[J].Studies in Nonlinear Dynamics&E-conometrics,2007,11(1).
[5]国家统计局数据库[EB/OL].http://www.stats.gov.cn/tjsj/ndsj/.
[6]王黎明,王连.应用时间序列分析[M].上海:复旦大学出版社,2009.
[7]王斌会.R语言统计分析软件教程[M].北京:中国教育文化出版社,2006.
[8]周巧.湖北省GDP总量的时间序列预测模型的比较分析[J].中南财经政法大学研究生学报,2009,(4).
[9]Hui zou,Yuhong Yang.Combining Time Series Models for Forecasting[J].Internayional Joural of Forecasting,2002,(2~4).

