基数约束下基于CVaR度量的投资组合优化模型

王 波，高岳林

（北方民族大学 信息与系统科学研究所，银川 750021）

0 引言

投资组合选择是现代金融理论的核心问题之一,主要解决的问题就是如何把一定数量的资金分配到不同的资产当中去,使得在小于某一给定的风险水平下最大化收益或者在收益满足一定阈值下最小化风险。因而,如何度量风险就成为非常重要的课题。

风险价值［1］VaR反映一项资产或资产组合在一定的持有期内、给定的置信水平下潜在的最大损失。作为VaR的改进,Uryasey与 Rockafellar［2］提出了条件风险价值 CVaR的优化投资组合的模型,并得出CVaR最优化投资组合与VaR最优化投资组合近似一致的结论。其含义是：组合损失超过VaR的条件均值,也称为平均超额损失,平均短缺或尾部VaR,它反映了损失超过VaR阀值时可能遭受的平均潜在损失的大小。CVaR是一致性的风险度量,已成为金融风险度量的有力工具。

近年来,国内关于基于条件风险价值度量的投资组合以及考虑实际市场摩擦如交易成本方面的文章很多,但是对于考虑基数约束和整手交易下的投资组合问题研究相对较少。胡支军,张珣解决了基数约束下的指数追踪问题,王懿［4］,陈志平等研究了多元t分布下带有基数约束的投资组合问题。本文根据我国实际证券市场条件,考虑整手买入交易和折线交易费用［5］,建立了带有基数约束的投资组合优化模型,利用进化算法求解并进行了实证分析,数值结果表明模型的合理性和算法的有效性。

1 条件风险价值简述

设 f（x，y）是在决策向量 x下的损失函数,其中,向量可以看成是组合中各资产的头寸或者权重，x∈X⊆Rn，X为可行集。向量表示对影响损失的市场因子,如市场价格或收益率。对每一个x，由y引起的损失f（x，y）是R上服从某一分布的随机变量。为方便起见,假设y的概率密度函数为p（y），则损失f（x，y）不超过某一阈值△p的概率为：

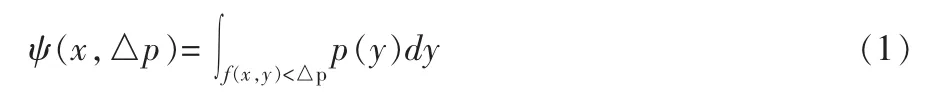
作为在x固定时△p的函数,ψ（x，△p）是与 x对应的损失的累积分布函数,关于△p非减右连续,与给定置信水平α下的损失对应的α-VaR与α-CVaR值分别为：

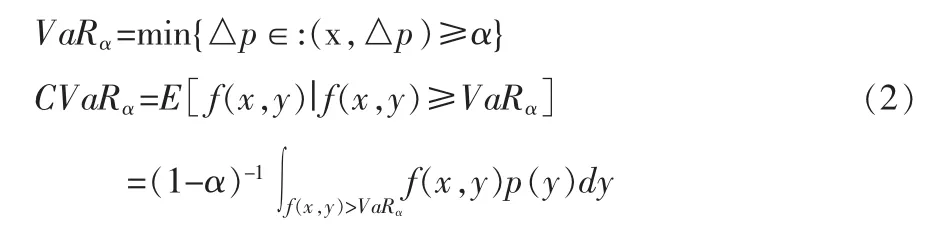
2 基于CVaR度量的投资组合优化模型建立

为了叙述方便,我们做以下符号解释,Qi，i=1，2，…，n 代表第 i种股票;ri，i=1，2，…，n 代表 i种股票的收益率;Pi，i=1，2，…n 代表 i种股票的价格;dbi，i=1，2，…n 代表买入第 i种股票所要征收的交易费用；ratio代表投资在一只股票上的资金比例上限;C代表初始资本（单位：元）；a代表置信水平;Zi={0，1}，Z z代表（0，1）整数变量；l和 u 代表股票持有种数的上下限;k1,k2代表股票的持有量的上下限。

2.1 目标函数

本文假设资产收益率为正态分布,我们在文献的基础上得出本文的目标函数。

记 r=（r1，r2…n） 为收益率向量,x=（x1，x2…n），x∈z为决策变量,假设 rN（μ,V）,其中为组合的期望收益,V为r的方差协方差矩阵,则收益（x）），其中，σ2（x）=（Px）V（Px）PxT，Px=（P1x1，P2x2…Pnxn）。 因此损失f=-记买入证券时的交易费用为则净收益为xi我们给出VaR和CVaR具体公式：

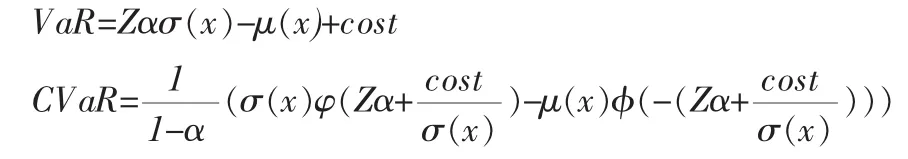
其中,Zα为标准正态分布的α下侧分位数，φ（·）为标准正态分布下的密度函数,φ（·）为标准正态分布下的分布函数。

2.2 约束条件

（1）收益约束

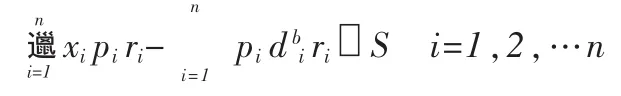
（2）资产价值约束

（3）资产投资比例约束

（4）基数约束

（5）不允许卖空约束

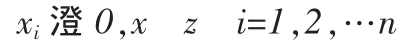
综上我们给出带有基数约束的投资组合模型

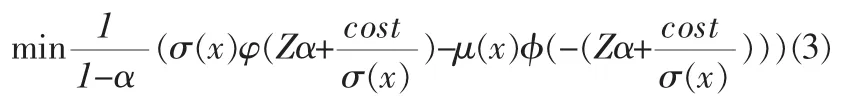
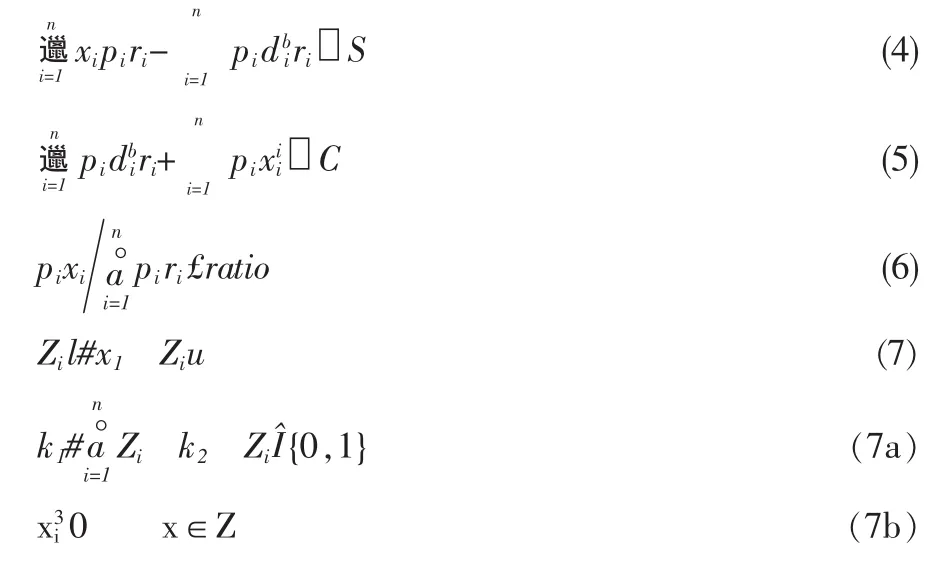
其中 i=1，2，…n.

3 算法描述

3.1 自适应差分进化算法简介[7]

差分进化算法[8-9]是由Rainer Ston和Kenneth price为求解切比雪夫多项式而于1995年共同提出的一种浮点矢量编码在连续空间进行随机搜索的优化算法。DE的原理简单,受控参数少,实施随机、并行、直接的全局搜索,易于理解和实现。DE算法的个体由实值向量组成,它们的维数D即为目标函数变量的个数,NP为种群的规模,由用户自己设置。我们给出解决整数规划的自适应差分进化算法如下:

3.1.1 变异操作

设当前进化个体为xit，i为当前个体在种群中的序号，t为当前进化代数。从当前进化个体重随机选取三个个体xt，取这两个个体向量的差经缩放因子F放大后加到第r1个个体向量上得到变异个体

其中,t代表当前迭代代数,T最大迭代代数,round（·）为取整函数。

3.1.2 交叉操作

变异后的个体ut+1i和种群中当前的进化个体以离散交

3.1.3 选择操作

3.2 约束处理

综上,我们给出求解模型的自适应差分进化算法实现过程如下。

第1步：定义差分进化算法中包含的粒子数目和维数。

第2步：设定变异概率值和缩放因子上下限值。

第 3步：用 round（rand（））命令产生一个每行元素中 1的个数之和在k1到k2之间的矩阵A。

第 4 步：用 round（l+（u-1）+*rand（））产生一个每行元素在l到u之间的矩阵B，其中l为大于0的整数。

第5步：将上述产生的两个矩阵A和B中的元素按照各自的位置对应相乘得到矩阵 C,此过程中已经保证约束（7）、（7a）、（7b）成立。

表1 不同置信水平下的计算结果

第6步：计算出满足约束的粒子的适应值.将适应值最小的个体信息和对应的适应值记录下来。

第 7 步：按照（8）、（9）式进行交叉操作产生实验个体,并判断实验个体trail的每一维是否在l到u之间,如果超出边界约束将该个体的当前维赋值为 round（l+（u-1）+*rand（）。

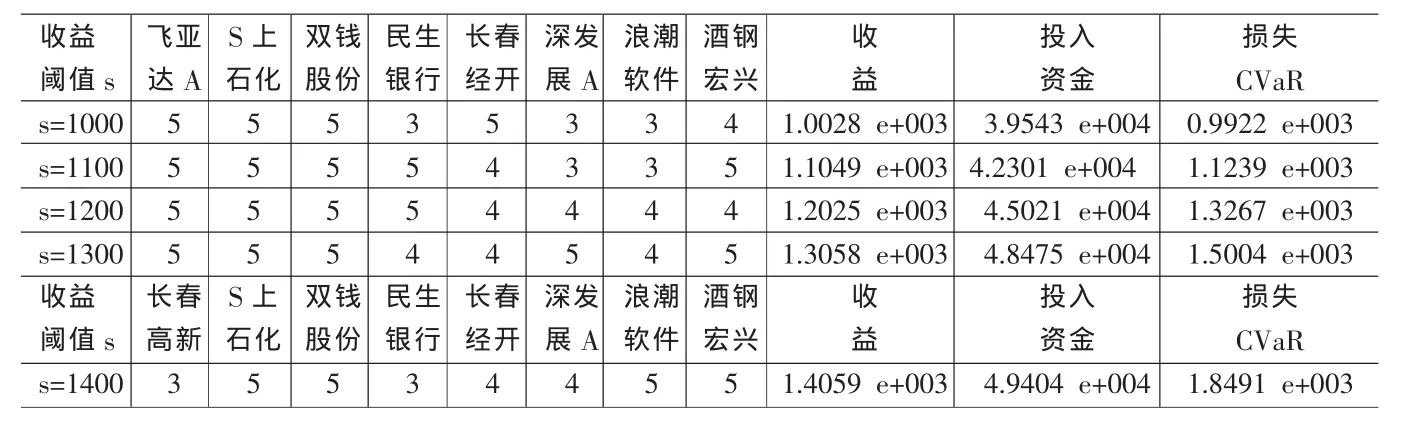
表2 不同收益阈值下的计算结果

第8步：（1）找出上述实验个体trail中非零元素个数,如果非零元素个数超出边界约束k1,k2,我们将按照第3步，第4步的做法产生一个新的个体trail1

（2）对上述产生的个体trail1进行（6）式的约束判断,如果满足执行第9步,否则,按照第3步,第4步的做法产生一个新的个体trail1,直到满足（6）式。

第 9步：按照（10）式进行选择操作,找出最优个体和最有个体对应的最优值。

第10步：不断更新个体的最优值,直到满足程序的终止条件,输出结果。

表3 收益阈值s=1500下的计算结果

表4 不同置信水平和不同收益阈值下的计算结果

4 实证分析

4.1 资产选取

为了分散风险,本节挑选不同行业、不同流通盘的股票进行投资,选取了沪深股票市场八支股票进行投资。十六支股票分别是：长春高新（000661）,新大陆(000997),飞亚达A(000026),S上石化(600688),东方电气(600875),双钱股份(600623),民生银行(600016),长春经开(600215),深发展A(000001),曙光股份(600303),浪潮软件(600756),酒钢宏兴(600307),隆平高科(000998),招商地产(000024),华夏银行(600015),中化国际(600500)。

4.2 数据预处理和算法参数设置

我们选取十六支股票2009年3月20至2009年7月31日20周的收盘价作为计算数据.我们用以下表达式计算股 票 的 周 收 益 率 ri，t=ln（pi，t-ipi，t）,其中pi，t和pi，t-i分 别 代 表 第 i支股票（i=1，2，…，16）t和 t-1 时刻的周收盘价.我们用MATLAB 7.0进行编程计算,算法中参数设置为：种群规模N=80,迭代代数 gen=500,缩放因子 F_max=0.8，F_min=0.4，变异概率CR=0.6惩罚因子sigma=106。

4.3 实验结果分析

我们将初始资金C=50，000（单位：元）,投资资产数目上下限设定为k1=5,k2=8(单位：手,1手=100股),持股数量上下限设定为l=2,u=5,ratio=0.2.

（1）数值试验中,我们首先将期望收益收益率阈值设定为s=1400元,由表1知,在不同的置信度水平下,我们得到投资的资产和买入量,以及收益值、损失值、投入资金值(单位:元).从损失值看,高的置信度表示投资者越厌恶风险,从而估计的风险就越大,这也反映了对于保守的投资者而言,他们将会选择较大的置信度。从投入资金值、收益值上分析,都满足模型中（4）、（5）的约束,从而也说明算法的运行结果是可行的。

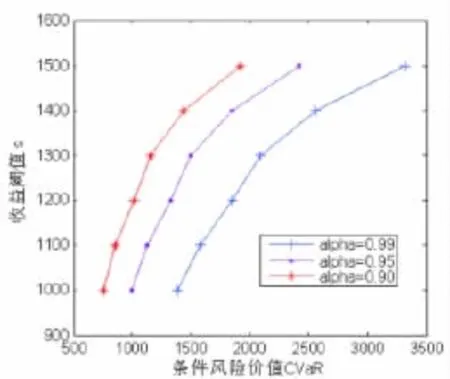
图1 不同置信水平下的风险有效边缘

(2)在置信水平αlpha=0.95水平下,表2,表3分别给出了收益率阈值s从1000元增加到1500时,所投资的资产和买入量,以及收益值、损失值、投入资金值(单位:元)。首先,随着收益阈值s的增加,损失值也不断增加,投入资金值也增加,这也满足高投入高产出,高风险高收益的原则。其次,投资的股票只数也从八只减小到了六只,趋于集中,相对而言不利于分散风险,所以对应的风险损失值也会增大。

（3)表4我们给出了不同置信水平下,收益率阈值 s从1000增大到1500时,对应的CVaR值,从表4中可以看出,随着收益率的增加,条件风险价值CVaR值也随着增加。根据表4数据绘制出收益风险的有效边缘见图1,从图1可以看到,置信水平越小,投资组合有效边缘越靠近图形的左上方,这是因为置信水平越高,投资者厌恶风险的程度越高。在相同的期望收益下,置信水平较低的对应的风险也相应较小,这也符合理论研究结果。

由上述分析我们可知,模型和运行的结果也是合理的,自适应差分算法对解决我们提出的模型是合理的。

5 结论

本文用CVaR来度量投资组合的风险,考虑了我国证券市场不允许卖空的条件,建立带有基数约束的考虑整手买入的投资组合模型.利用罚函数处理约束收益,运用差分进化进行求解,并采用沪市和深市的十六种股票作为备选股票。数值结果表明了模型的合理性和算法的有效.我们计算出了不同收益阈值下的买入量、收益值、损失值、投入资金值,为投资者提供了决策参考。

[1]Philippe J.Value atRisk:the New Benchmark forControlling Market Risk[M].Chicago:Irwn Prefessional，1996.

[2]Rockafellar R T，Uryasev S.Optimization of Conditional Valueat-Risk[J].The Journal of Risk，2000.

[3]胡支军，张珣.带有基数约束的指数跟踪问题及其粒子群算法求解[J].黑龙江大学自然科学学报，2009，26（5）.

[4]YiWang，Zhiping Chen,Kecun Zhang.A Chance-constrained Portfolio Selection Problem Under T-distribution[J].Asia-Pacific Journal of Operational Research，2007，24（4）.

[5]高岳林，苗世清.考虑交易费用的投资组合优化模型研究[J].商业研究，2010，396（4）.

[6]刘小茂，李楚霖，王建华.风险资产组合的均值－CVaR有效前沿(I)[J].管理工程学报，2003，17（1）.

[7]高岳林，刘俊芳.自适应差分进化算法[J].河北工程大学学报，2008，25（4）.

[8]R.Storn,K.Price.Differential Evolution-a Simple and Efficient Adaptive Scheme for Globle Optimization over Continuous Spaces[R].Technical Report,International Computer Seience Institute，1995，（8）.

[9]R.Storn,K.Price.Differential Evolution-a Simple and Efficient Adaptive Scheme for Globle Optimization over Continuous Spaces[J].Journal of Global Optimization，1997，11（4）.