基于遗传算法和小波神经网络的语音识别研究
斯芸芸,徐道连,周卓然
(重庆大学 光电工程学院,重庆400030)
语音识别是要让机器“听懂”人类的语音并做出正确的反应,其终极目标是实现人类与机器的自然交流。随着科学技术的发展,语音识别技术正逐步形成一套比较完整的理论体系,其实用产品也相继推出。
现代语音识别技术以人工神经网络(ANN)为主要发展趋势,自上世纪90年代,神经网络已经成为语音识别的一条重要途径[1]。目前具有代表性的神经网络主要有BP神经网络和RBF神经网络。为了提高网络训练速度和语音识别的识别率,神经网络模型不断地被优化。小波神经网络(WNN)是BP神经网络的一种优化模型,它采用小波函数作为激励函数,具有以下一些优点:(1)高度的并行性;(2)高度的非线性映射功能;(3)十分强的自适应功能;(4)良好的容错性和联想记忆功能;(5)小波函数具有时频局部特性和变焦特性[2]。目前神经网络方法对网络隐层节点数、连接权值(包括阈值)以及学习率的依赖性较大,容易导致陷入局部极小、收敛速度慢,甚至不收敛的状况。而遗传算法具有很强的宏观搜索能力,能以较大的概率找到全局最优解[3,4]。为了克服神经网络的不足,本文将两者结合在一起,提出了一种训练神经网络的混合算法——GA-WNN算法。
1 语音识别的基本原理
语音识别系统实质上是一种模式识别系统,与常规模式识别系统一样包括特征提取、模式匹配、参考模式库等三个基本单元。基于神经网络的语音识别系统识别功能要经过从特征参数提取到应用识别算法进行识别的过程,它的系统原理框图如图1所示。

图1 语音识别系统原理框图
由图1可知,要进行语音识别,首先要对输入的语音信号进行预处理。预处理主要包括预加重、加窗、分帧和端点检测等过程。
(1)预加重:预加重的主要目的是提升语音信号中的高频部分进而减小噪声 (主要是50 Hz或60 Hz的工频干扰),提高信噪比。本文选择用预加重数字滤波器来实现对语言信号的预加重,若S(n)为预加重前语音信号,则经过预加重滤波器的信号R(n)为∶
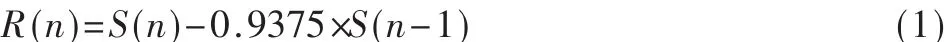
(2)加窗和分帧:语音信号随时间变化而变化,研究表明语音信号通常可以假定为短时平稳,通常认为在10 ms~30 ms时间长度内是相对平稳的。分帧可用窗函数乘以语音信号来形成加窗的语音信号。本文选用汉明窗(Hamming)作为加窗函数,用汉明窗将语音切割成长短一致的语音帧,每帧语音采样点数为256点,帧移为128点。
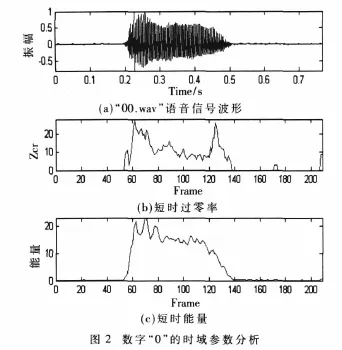
(3)端点检测:端点检测的目的是判断找到有用语音信号的起点和终点,然后根据语音段的起点和终点,分离出真正有用的语音信号,为后续的语音识别奠定可靠的基础。本文采用目前比较流行的双门限端点检测算法,通过语音信号的短时平均能量和短时过零率来判断语音信号的起点和终点。图2和图3分别是一个数字“0”的时域参数分析及其端点检测结果。语音信号是用多媒体声卡在比较安静的实验室环境下录制的,其信噪比较高,双门限端点检测算法可以较准确地判断出语音信号的起始位置,由图可知,实验结果与理论分析一致。
语音信号经过预处理后,将进行语音识别中的一个重要环节——特征参数提取。好的特征参数不仅能很好地反应语音特征,而且计算方便,这对系统的实现非常重要。常用的特征参数包括线性预测系数(LPC)、线性预测倒谱系数(LPCC)和美尔频率倒谱系数(MFCC)。综合三者的优缺点,本文选用MFCC作为研究的特征参数。每帧语音信号分别提取12维的MFCC作为特征向量,为减少运算量,每个语音信号只选择中间的6帧来进行实验。
2 语音识别中的小波神经网络构造
小波神经网络是以小波函数为神经元激励函数的前馈网络模型,与基于Sigmoid函数的BP网络相比,具有较强的函数逼近能力和容错能力,同时具有结构收敛可控性和收敛速度快等优点。小波神经网络构造主要包括网络层数、输入节点数、输出节点数、隐层节点数、初始权值、学习速率及期望误差的选取[5,6]。
(1)网络层数:理论上早已证明,具有偏差和至少一个隐含层加上一个线性输出网络就能够逼近任何有理函数。本文是针对数字孤立词的识别,小波神经网络采用3层结构,包括一个输入层、一个隐含层和一个输出层。输入层激励函数为线性变换(输出=输入),隐含层激励函数为小波函数,输出层激励函数为Sigmoid。
(2)输入节点数:输入层节点数与所选取的语音信号特征参数的维度和阶数有关。本文中每个语音信号都得到相应的6个12维一阶MFCC系数,故输入层的节点数为 6×12=72。
(3)输出节点数:输出层的节点数取决于输出数据的类型和表示该类型所需的数据大小。本文数字孤立词识别的10个数是0~9,所以设定输出节点数为10,分别对应于 0~9。
(4)隐层节点数:通过采用一个隐层,增加其神经元个数的方法来达到网络训练精度的提高。隐层的神经元个数选择可以通过仿真试验来确定,也可以用以下公式[5]作为参考:

其中,m为输入层节点数,n为输出层节点数,a为取 1~10的常数。本文采用公式(2)来确定隐层节点数,已知输入节点数为72,输出节点数为10,a取常数5,因此隐层节点数n1=14。
(5)初始权值:由于系统是非线性的,初始值对学习是否达到局部最小、是否能收敛以及训练时间的长短关系很大。一般总是希望经过初始加权后的每个神经元的输出值都接近于零,所以,通常初始值取(-1,1)之间的随机数。
(6)学习速率:学习速率决定循环训练中所产生的权值变化量。大的学习速率可能导致系统的不稳定,小的学习速率虽然会导致收敛速度慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小值。所以一般情况下,学习速率的选取值范围在0.01~0.8之间。本文设定学习速率为0.8。
(7)期望误差的选取:在设计网络的训练过程中,期望误差也应通过对比选取一个合适的值,可以同时对两个不同时期的期望误差的网络进行训练,通过综合考虑来确定。本文研究的期望误差为0.001[7]。
3 基于遗传算法和神经网络的语音识别
小波神经网络的学习对网络隐层节点数、初始权值(包括阈值)、伸缩和平移因子以及学习速率的依赖性较大,致使其全局搜索能力弱,易陷入局部极小,收敛速度慢甚至不收敛,而遗传算法具有很强的宏观搜索能力,能以较大的概率找到全局最优解,因此把遗传算法和小波神经网络相结合,采用遗传算法对网络的初始权值(包括阈值)进行优化处理,用小波神经网络完成给定精度的学习。
3.1 遗传算法实现的关键技术
(1)编码方案
编码对网络进化过程的性能和效率影响很大,因此,编码技术是连接权值进化过程中需要解决的首要问题和关键步骤。考虑到网络参数的规模较大,若遗传算法采用二进制编码,会导致染色体长度偏长、搜索空间大、搜索效率低等问题,本文中小波神经网络的节点数和结构已经固定,可以采用实数编码方案,将网络的权值和各节点的阀值依次排列得到一个向量。
(2)适应度函数的选择
衡量网络性能的主要指标是网络的实际输出与期望输出值之间的误差平方和。神经网络中误差平方和越小,则表示该网络性能越好。
定义适应度函数为:

(3)遗传操作
选择算子:从当前种群中选择优胜(即适应度高)个体而淘汰劣质个体。目前常用的选择算子有以下几种:适应度比例选择法、最佳个体保存法、期望值法与排序选择法等。本文采用适应度比例选择法来进行选择操作[3]。
交叉算子:交叉是通过替换重组两个父代个体的部分结构而产生新的个体。在遗传算法中,交叉操作是最主要的遗传操作。交叉率Pc是指各代中交叉产生的后代数与种群规模之比,这个概率表明有 Pc×pop_size(种群规模)个染色体来进行交叉操作。常用的交叉率取值范围为 0.6~1.0,在本文中 Pc取 0.6。
变异算子:变异就是对群体中的个体串的某些基因位上的基因值作变动。变异率是指种群中变异的基因数占总基因数的比例,其值控制了新基因引入的比例,这个概率表明有Pm×pop_size(种群规模)个染色体来进行变异操作。常用变异率的数量级范围为0.1~0.001,在本文中Pm取0.1。
(4)终止条件
采用给定的迭代次数和适应度来控制遗传算法的终止。如果迭代次数已经用完或某代的最优个体的适应度值大于等于预先给定的值,算法就结束。
3.2 GA-WNN算法实现的步骤和流程
采用遗传算法来优化小波神经网络的权值和阈值,具体实现的步骤如下:
(1)设定参数:种群规模pop_size=100,交叉概率 Pc=0.8,变异概率 Pm=0.1。
(2)随机产生一组实值串种群,每一个个体由网络的初始权值和阀值构成。
(3)对实值串中的个体进行解码,生成相应的网络结构,网络结构为72-14-10。
(4)运行网络,根据式(4)计算群体个体的适应度值,评价网络性能。
(5)根据适应度大小,通过相应的选择算法进行选择操作,以交叉概率Pc执行交叉操作,以遗传概率Pm执行变异操作,保留适应度大的个体产生下一代种群,形成下一代网络。
(6)如果网络误差满足要求或达到一定的进化代数,则停止进化,输出结果;否则重复操作步骤(3)~步骤(5)。
(7)将GA优化后的初始权值(包括阈值)作为小波神经网络使用的参数。
3.3 基于GA-WNN算法的语音识别过程
将本文提出的新算法(GA-WNN算法)应用于语音识别,具体的识别过程如下:
(1)语音数据由三男二女的发音(0~9共 10个数字的普通话发音)数据组成,每个音每人发20遍,共计1 000次发音,其中以每人每个发音的前10次作为训练样本,后10次作为测试样本。
(2)用数字滤波器分别对两组语音数据进行预加重,再通过加汉明窗对语音信号进行分帧,然后逐帧计算语音信号的MFCC系数,并将其保存。
(3)构造一个三层的小波神经网络,设置初始的网络参数,网络结构为72-14-10,取学习速率为0.8,训练误差精度为0.001。
(4)对每个人的语音特征系数用 WNN算法来训练网络,同时用遗传算法来优化神经网络的权值,直到网络收敛并达到期望的训练误差精度0.001,保存最优权值。每个语音信号对应一组网络权值。
(5)在网络的输入层中输入语音特征参数系数,分别调用已保存的网络权值计算出结果得出网络输出矩阵,与期望输出矩阵逐一比较,误差最小的那个语音信号为识别结果。
4 仿真实验结果
为了验证GA-WNN算法的优越性,对算法的性能进行了测试,并与小波神经网络算法的性能进行了比较。
仿真实验是针对非特定人的孤立词数字语音识别,语音数据由三男二女的发音 (0~9共10个数字的普通话发音)数据组成,本实验是在PC机上进行,通过PC话筒输入,每个音每人发20遍,共计 1 000次发音,其中以每人每个发音的前10次作为训练样本,后10次作为测试样本。
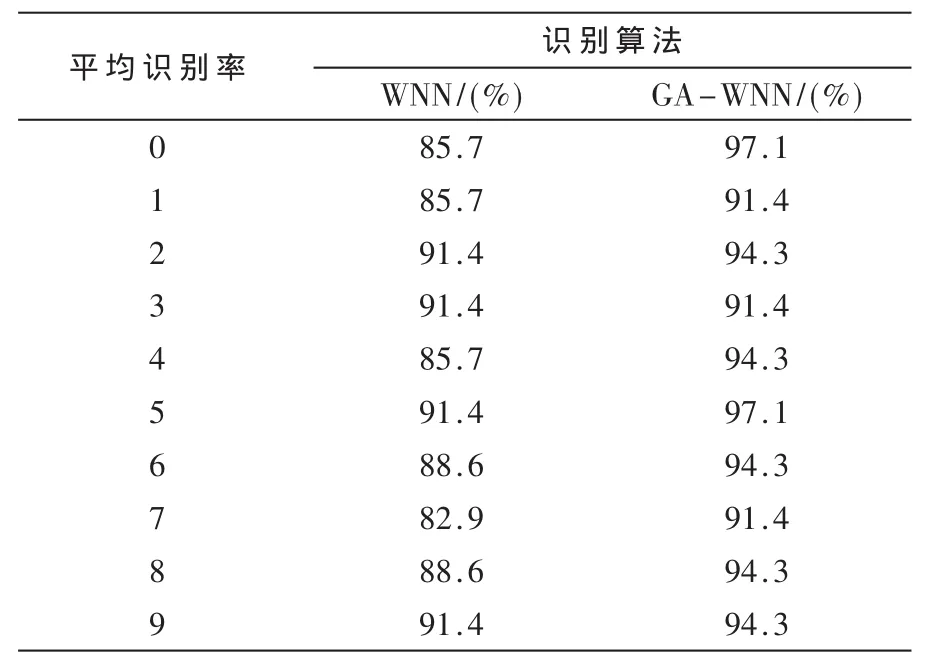
表1 孤立词识别结果
经过试验仿真,得到实验结果如表1。对实验结果进行对比分析,发现基于GA-WNN算法的语音识别系统得到了相对较高的识别率,基于GA-WNN学习算法只迭代了105次便使得误差为0.001,而小波神经网络算法需要迭代741次才达到相同的误差精度。由此可见,相比小波神经网络算法,基于GA-WNN算法,无论是在精度上还是收敛速度上,都取得了更好的效果,同时该算法还避免了局部极小,从而能快速地找到最优解,降低学习时间。
从实验结果得出:对于孤立词的识别,WNN的平均识别率为88.6%,而GA-WNN的平均识别率达到94.0%,明显高于WNN的识别率,验证了理论的正确性。
将遗传算法和小波神经网络结合起来形成GAWNN算法,仿真实验结果表明,此算法在孤立词的识别中不仅缩短了识别时间还有效地提高了系统的识别率。该算法还可以应用于图像处理或其他领域,需要作进一步的验证。
[1]ROBERT E U.Application of artificial neural networks in industrial technology[J].IEEE Trans,1994,10(3)∶371-377.
[2]唐军.基于HMM与小波神经网络的语音识别系统研究[D].南京:南京理工大学,2007.
[3]BRINDLE A.Genetic algorithms for function optimization[M].Ph.DDissertation,University of Alberta,1981.
[4]SELOUANI TS A,SHAUGHNESSY D O.Robustness of speeeh recognition using genetie algorithm and a mel-cepstral subspace approach[J].ICASSP,2004,12(2):201-204.
[5]赵峰.遗传神经网络在语音识别中的研究[J].电脑知识与技 术,2008,3(4)∶774-776.
[6]刘俊华,颜运昌,荆琦.遗传算法与神经网络在语音识别中的应用[J].机电工程,2007,24(12)∶20-24.
[7]韩志艳,王健,伦淑娴.基于遗传小波神经网络的语音识别分类器设计[J].计算机科学,2010,37(11)∶243-246.

