基于OpenMP多核架构下并行蚁群算法研究*
赵 辉 , 徐俊刚
(1.中国科学院研究生院,北京 100049;2.北华航天工业学院 计算机科学与工程系,河北 廊坊065000)
蚁群算法是由意大利学者DORIGO M提出的,主要应用于求解组合优化问题,该算法首先应用在旅行商(TSP)问题并取得较好的效果。蚁群算法不仅能够智能搜索、全局优化,而且具有稳健性、正反馈、分布式计算、易与其他算法结合等特点。然而该算法基本上都是基于单CPU串行执行的,在求解问题规模较大时,存在收敛速度较慢等缺点。
随着多核处理器的普及,如何让传统的单CPU串行程序充分发挥高性能多核处理器的功效,是一个现实而严峻的问题。解决这一难题的有效途径之一就是并行计算。为了将计算能力最大化,需要将算法代码中的计算任务划分为多个部分,并交由多个处理器核心同时处理。要实现这一目标,需要一种全新的程序设计模型,目前比较流行的并行程序设计模型之一就是用于共享内存编程的OpenMP。本文将对基于OpenMP的多核架构下并行蚁群算法的实现进行介绍,并通过对大规模TSP问题进行实验验证OpenMP多核并行计算技术能够大大提高蚁群算法的运行效率。
1 OpenMP简介
OpenMP是一种面向共享内存以及分布式共享内存的多处理器多线程并行编程语言,具有良好的可移植性,同时支持Fortran、C和 C++。OpenMP程序设计模型提供了一组与平台无关的编译指导、指导命令、函数调用和环境变量,可以显式地指导编译器利用应用程序中的并行性。它能够为编写多线程应用程序提供一种简单的方法,通过编译指导语句,可以将串行的程序逐步地改造成一个并行程序,从而减少程序编写人员的负担。
OpenMP程序开始于一个单独的主线程。主线程会一直串行地执行,直到遇见第一个并行域才开始并行执行。并行域表示该部分程序计算量大,需要多个处理器共同处理以提高效率和运行速度。并行域以外的部分表示该部分的程序不适宜或者不能并行执行,只能由一个处理器来执行。主线程创建一组并行线程,然后并行域中的代码在不同的线程中并行执行,当主线程在并行域中执行完后,它们可能被同步或被中断,最后只有主线程在执行。OpenMP的并行执行过程如图1所示。例如对于 for循环语句 for(int i=0;i<100;i++),按常规串行处理时,i要按顺序执行从0~99。如果在双核环境下,则分成两个线程,两个CPU执行核同时处理,核0执行i从0~49,核 1执行 i从 50~99,理论上可以节省一半的时间。而这种从串行执行到并行执行的改变,只需要一条OpenMP编译指导指令就可以完成。编译指导语句的含义是在编译器编译程序时,会识别特定的注释,而这些特定的注释就包含着OpenMP程序的一些语义。例如在C/C++程序中,用#pragma omp parallel来标识一段并行程序块。在一个无法识别OpenMP语义的普通编译器中,会将这些特定的注释当作是普通的注释而被忽略。因此,如果仅仅使用编译指导语句,编写完成的OpenMP程序就能够同时被普通编译器与支持OpenMP的编译器处理。这种性质带来的好处就是可以用同一份代码来编写串行或者并行程序,或者在把串行程序改编成并行程序时,保持串行源代码部分不变,大量的工作都由编译器自动执行,从而极大地方便了程序编写人员。
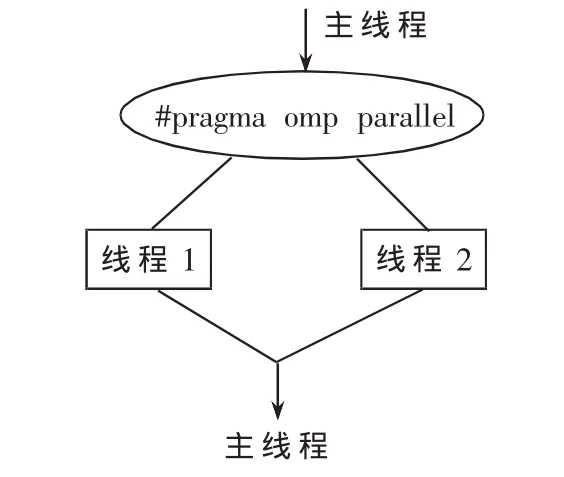
图1 OpenMP并行执行模型
2 蚁群算法
2.1 基本原理
根据仿生学家长期的研究发现∶蚂蚁虽然没有视觉,但运动时会在路径上释放出一种名为信息素的特殊分泌物来寻找路径。蚂蚁走的路径越长,则释放的信息素数量越小。当后来的蚂蚁再次碰到这个路口的时候,选择信息素数量较大路径的概率就会相对较大,这样形成了一个正反馈机制。蚂蚁之间交换着路径信息,最终通过蚁群的集体自催化行为找出最优路径。
2.2 蚁群算法的数学模型
为了能够清楚地表达蚁群算法的数学模型,本文借助了经典的TSP问题。给定n个城市的集合{1,2,3,…,n-1}及城市之间环游的花费 Cij(0≤i≤n-1,0≤j≤n-1,i≠j)。TSP问题是指找到一条经过每个城市一次且回到起点的最小花费的环路。若将每个顶点看成是图上的节点,花费Cij为连接顶点Vi和 Vj边上的权,则TSP问题就是在一个具有n个节点的完全图上找到一条花费最小的汉密尔顿路。
设在TSP问题中有n个城市和m个蚂蚁,把m个蚂蚁随机放在n个城市中(m≤n)。每个蚂蚁的行为符合下列规律:根据路径上的信息素浓度,以相应的概率来选取下一步路径;不再选取自己本次循环已经走过的路径为下一步路径。用禁忌表tabuk(k=1,2,…,m)来记录蚂蚁k当前所走过的城市,集合tabuk随着进化过程作动态调整;当完成了一次循环后,根据整个路径长度来释放相应浓度的信息素,并更新走过的路径上的信息素浓度。
现用τij(t)表示在t时刻边(i,j)上的信息素浓度。经过n个时刻,当蚂蚁完成了一次循环之后,相应边上的信息素浓度必须进行更新处理,对旧的信息进行削弱,同时将最新的蚂蚁访问路径的信息素加入到τij(t),得到:

式中ρ为一个取值范围在0~1之间的常数,表示信息素的残留部分,(1-ρ)表示信息素的挥发程度,其中∶
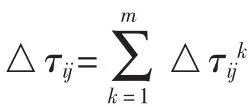
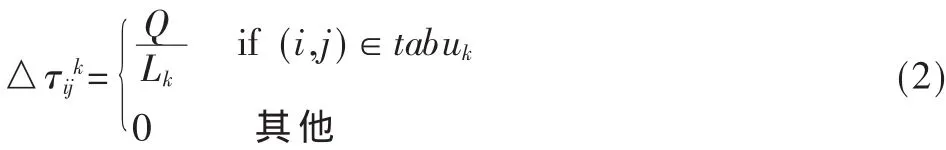
式中,Q是一个常量,用来表示蚂蚁完成一次完整的路径搜索后,所释放的信息素总量;Lk是第k个蚂蚁的路径总花费,它等于第k只蚂蚁经过的各段路径上所需的花费Cij的总和。如果蚂蚁的路径总花费越高,则其在单位路径上所释放的信息素浓度就越低。很显然,蚂蚁不会在其没有经过的路径上释放信息素。
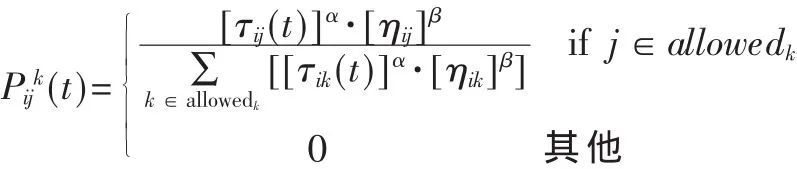
式中,ηij=1/Cij,Cij为经过路径(i,j)所需的花费。α和β两个参数,分别用来控制信息素和路径长度的相对重要程度。allowedk是第k只蚂蚁下一步可以选择的城市的集合 。 allowedk={0,1,2,…,n-1}-tabuk。
3 基于OpenMP的并行蚁群算法实现
蚁群算法本身具有很高的并行性,所有蚂蚁能够独立构建问题的可行解,每个蚂蚁在构建解的过程中只与当前的信息素和启发函数有关,只有在所有蚂蚁均完成了可行解的构造之后,信息素更新时存在蚂蚁间的通信。因此可以将各个蚂蚁构建可行解的过程分配到不同的线程中并行执行。
在蚁群算法中,运算量主要集中在每一只蚂蚁重新计算建立回路以及每次循环结束前更新路径上的信息素,即串行蚁群算法的大部分计算集中在for循环部分,同时也是算法复杂度的主要来源。当节点数目很大时,可以将计算循环分割成若干个部分,每个部分就可以在一个独立的硬件线程上完成。本文给出基于OpenMP的并行算法设计,目的是在不改变算法行为的前提下提高算法的执行效率,充分利用多核处理器的优势。基于OpenMP的并行蚁群算法的主要过程为∶
(1)初始化过程∶通过OpenMP中的编译指令 #pragma omp parallel for对算法进行初始化。初始化工作主要包括计算任意两个节点间的距离、计算τij的初始值、把m个蚂蚁随机放到n个城市上和设置蚂蚁的禁忌表tabuk。通过OpenMP中的#pragma omp parallel for对初始化操作进行并行处理,把初始化工作中大量的循环迭代和循环赋值任务分配到不同的处理器核上并行执行。
(3)更新最短路径。当所有蚂蚁遍历完所有节点后,通过OpenMP中的编译指令#pragma omp parallel for并行计算每个蚂蚁走过的总路径长度Lk,并更新找到的最短路径。
(4)更新信息素。计算蚂蚁产生的信息增量,更新路径上的信息素。节点间的信息素是残留的信息素和信息素增量的叠加。残留信息素的循环计算是独立的,可以通过#pragma omp parallel for进行并行处理。而信息素增量的计算需要各个蚂蚁之间的通信,为了避免并行过程中频繁的通信,不使用OpenMP并行优化,而采用串行计算。
(5)运行结束。若循环次数没有达到预定次数,则重复执行第(2)步,否则运行结束,打印最佳路径。
算法的执行过程如图2所示。

4 实验结果及分析
本文所设计的算法在Intel酷睿2双核E7500处理器上进行实验,串行蚁群算法和基于OpenMP的并行蚁群算法的实验比较结果如表1所示。实验结果表明:当问题规模比较小时,串行蚁群算法和基于OpenMP的并行蚁群算法的运行时间相差不大,但随着问题规模的扩大,并行算法的运行时间将会缩短到原来的50%左右,明显提高了算法的运行效率。
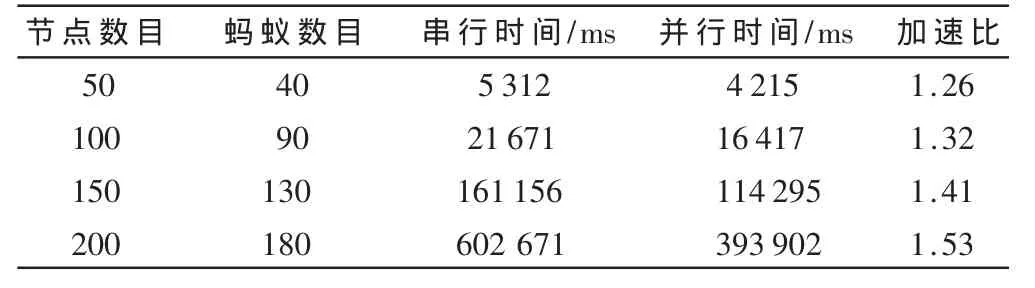
表1 串行蚁群算法和基于OpenMP的并行蚁群算法的比较
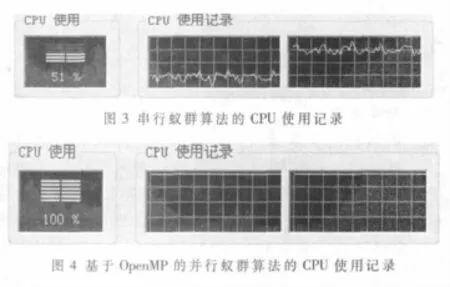
串行蚁群算法和基于OpenMP的并行蚁群算法在解决同样规模问题时,CPU的使用情况如图3和图4所示。结果表明:串行算法不能充分利用两个处理核心的资源,CPU的使用率在50%左右,造成了资源的浪费,而OpenMP设计的并行算法充分利用了两个处理核心资源,使CPU的使用率达到100%,这也正是蚁群算法运行效率提高的原因。
本文研究了一种基于OpenMP的多核架构下并行蚁群算法,并在TSP问题中对算法进行了验证。并行优化计算过程简单灵活,易于操作,而且充分利用了多核处理器的优势,提高了算法的运行时间效率,为解决大规模组合优化问题提供了可能。
[1]夏鸿斌,须文波,刘渊.基于多蚁群的并行 ACO算法[J].计算机工程,2009,35(22)∶23-28.
[2]黄亚平,王万良,熊婧.基于自适应蚁群算法的作业车间模糊调度研究[J].计算机仿真,2009,26(4)∶244-248.
[3]何丽莉,王克淼,白洪涛,等.基于 CMP的多种并行蚁群算法及比较[J].吉林大学学报(理学版),2010,48(5)∶787-792.
[4]多核系列教材编写组.多核程序设计[M].北京∶清华大学出版社,2007.
[5]姜长元.蚁群算法的理论及其应用[J].计算机时代,2004(6)∶1-3.
[6]阎芳,杨玺,陈蕾.基于 OpenMP的并行蚁群物流调度算法研究[J].物流技术,2010(13)∶91-93.
[7]李妮,高栋栋,龚光红.基于 TBB多核平台的并行蚁群算法 实 现[OL-EB].http∶//www.paper.edu.cn.

