基于广域信号的区域间低频振荡监视
常勇,吴靖,王超
(1.国家电网公司 运行分公司,北京 100053,2.杭州市电力局,浙江 杭州 310009;3.浙江省电力公司,浙江 杭州 310027)
当联络线传输功率过重时,同步发电机阻尼转矩不足而导致的低频振荡是限制跨区交换容量的瓶颈之一,它严重威胁到电力系统的安全稳定运行[1-3]。1996年北美大停电的初始阶段,主要潮流断面上均观察到明显的低频振荡现象,并最终导致大范围的电网解裂,而整个事故发展时间跨度有几十分钟。2003年美加大停电事后,对事故发展过程的调查表明,这次大停电事故也是由区域性故障逐步发展而来[4]。可以想见,如果在系统振荡发生的初始阶段及时判断发现动态不稳定现象,并经分析给出合理的控制策略,就能及时缓解故障对系统的冲击,避免故障大范围扩散。
传统上研究大型系统低频振荡问题常采用特征值分析的方法,如QR算法等。但是当前实际电力系统规模较大、维数较高、实际计算有较大困难,而在线辨识的方法则可以避免维数灾问题[5]。广域测量系统(Wide Area Measurement System,WAMS)给电力系统的实时动态监测控制手段带来了新的发展契机[6-8]。WAMS系统可以直接量测电力系统电压电流等相量,并且利用GPS同步授时,各数据量被加上同步绝对时间时标,数据间的理论时间误差只是GPS系统误差。测量数据较之SCADA测量数据精度及时间准确性大大提高,借助高速的通讯手段,这些数据可以用作全网动态实时监测的宝贵数据源[9]。
本文首先提出了实时同步监测和实时控制的双层低频振荡监控中心体系结构,然后比较了已有报道的若干种低频振荡实时监测算法,最后针对若干测试系统及一个实际系统小扰动后的时域响应曲线详细比较了Prony方法和ESPRIT方法辨识低频振荡的技术特性,获得了一些指导其在线应用的结论。
1 电力系统低频振荡监控系统结构
在全网同步相量监测的基础上,在线电压稳定控制、在线频率稳定控制、实时网架拓扑连通性分析、以及实时事件记录等高级功能都可以实现。构想中的全网实时低频振荡监控中心在概念上应该属于全网动态监控系统(AEMS)中的一个功能模块,在物理实现上,可以与其余高级功能共用PMU、数据集中器、网关、工作站等设备[10]。
特征值分析方法和模态辨识方法各有其优缺点:特征值分析可以获得详尽的系统信息,然而其耗时多,准确性取决于对电力系统模拟的精度。模态辨识的方法具有实时性好的优点,但是其分析结果受信号噪声影响较大。低频振荡监控中心的信号流程如图1所示。

图1 低频振荡监控系统信号流程图
实时的电力系统运行工况信号与EMS系统信号相结合,在线更新电力系统小扰动模型。在此基础上可以进行准实时的特征值分析以及时域仿真分析。特征值分析可以方便地得到整个系统的振型、阻尼、振荡频率等关键量,可以决定反馈信号、设计控制器结构以及控制施加地点。时域仿真结果同样可用于时/频域分析,其结果可以和实时反馈信号的时/频域分析结果相互校核。电力系统实时信号经过频域或时域分析后,结合在线准实时特征值分析的结果调整闭环控制器参数,然后系统将控制信号反馈回电力系统实现实时控制。直接对反馈信号进行时/频域分析速度较快,其结果可以作为在线监视以及在线调整控制器参数的主要依据。
2 电力系统低频振荡在线辨识方法
实现低频振荡实时监控的基础是振荡模式等特征量的实时在线辨识,模态辨识方法层出不穷,但是从辨识方法上归纳,主要可以分为基于模型参数的辨识方法和非参数化辨识方法。前者主要包括基于模型参数的AR方法[11-12]、Prony方法[13]。另外,近年来发展起来的子空间方法 (Subspace)也有其可取的优点[14],从本质上说,也属于基于模型参数的模态辨识方法。非参数化的方法以傅里叶变换算法为主,在其基础之上发展了滑动窗傅里叶变换(Sliding Window Fourier Transformer)等算法提高了算法的工程适用性[15]。
2.1 ESPRIT方法
ESPRIT方法(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)即基于总体最小二乘法——旋转不变技术的信号参数估计方法,是一种基于子空间的高分辨率的模式辨识算法,最初该算法多用于雷达信号处理[16],在文献[17]中将其应用到电力系统低频振荡特性辨识上。类似Prony算法,此方法可利用电力系统测量数据或者时域仿真数据分析电力系统的低频振荡问题,不受电网规模的限制,克服了传统特征值分析法的局限性。但ESPRIT是一种基于子空间的辨识方法,直接以数据序列构成的Hankel数据矩阵为基础,把信号空间分解为信号子空间和噪声子空间,理论上可以高精度地辨识电力系统中任意组合的衰减/非衰减正弦信号的频率、相位和幅值等参数信息,具有较强的抗噪声能力。它避免了求取信号的自相关矩阵(correlation matrix),简化了计算。另外ESPRIT方法采用奇异值分解(Singular value decomposition,SVD)等计算方法,数值计算稳定性和鲁棒性更好,能够在较短的信号长度内准确辨识出系统低频振荡的主导模式(dominant mode)。TLS-ESPRIT是ESPRIT的改进算法,作为谐波恢复,振荡衰减正弦信号参数估计的有效工具,目前已被广泛地应用于雷达阵列信号,语音信号,生物信号处理等场合[18]。TLS-ESPRIT算法近年来也被引入到电力系统中,应用于谐波和间谐波高精度检测,暂态信号分解[19]等场合。该算法的原理框图如图2所示。
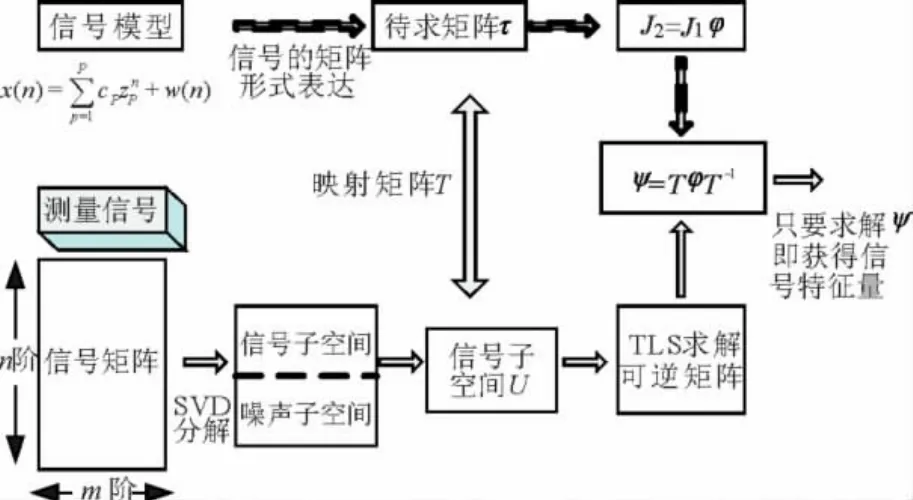
图2 ESPRIT算法的原理框图
2.2 Prony方法
Prony方法是用指数函数的线性组合来拟合等间隔采样数据的方法,可以从中分析出信号的频率、衰减因子、幅值和相位。和特征值分析方法相比,Prony方法是模态参数辨识的时域方法,不用求解大规模系统的特征值,其系统模型的阶数可以根据辨识的目的和需要等确定。Prony方法对实时测量的系统数据进行分析,最大的问题是如何避免噪声信号的影响[20-21]。
2.3 FFT方法
傅里叶变换算法是谱分析非参数化方法中常用的一种,它的优点很多,例如:对信号噪声不敏感;可利用FFT快速傅里叶算法,计算速度快,有利于在线使用;另外不易出现模型失配的情况。考虑到算法的栅栏效应,为了避免频谱泄漏,文献[22]利用滑动窗FFT算法提高了在线模态辨识的精度。
2.4 子空间方法
近年来子空间方法被广泛地应用于随机信号模型辨识,文献[14]给出了子空间模型辨识方法的主要原理及步骤。与传统方法相比,子空间方法具有数值稳定性好(采用QR算法、最小二乘法、以及奇异值分解等算法)、无须优化过程计算速度快、可以方便地进行多输入多输出(MIMO)系统辨识等优点。子空间方法的核心思想是首先基于输入输出数据构建系统状态相量,然后在此基础上求解最小二乘问题,得到系统的传递函数矩阵,最后求解此传递函数矩阵即可以获得表征系统动态特性的各量。子空间辨识基本算法主要有3种,即:MOESP(multivariable output error state space)、N4SID(numerical algorithm for subspace state space system identification)以及CVA(canonical variable analysis)。
3 在线辨识算法综合分析
3.1 在线辨识算法的普适要求
实际应用于电力系统辨识的算法则需要满足以下几个性能要求。
1)准确性。实际电力系统采样信号往往被噪声污染,通过上一节的分析,考虑到计算效率以及在线实现的方便性,Prony方法和ESPRIT方法更加适合于低频振荡的在线实时分析。笔者将以若干参考系统和一个实际系统为例,检验比较这两种算法的计算精度和实际效率。
从工程实际出发,不同辨识算法的比较主要从辨识精度和算法耗时两个角度评价。衡量分析结果有两个指标:信噪比和百分比误差。假设真实数据为x(k),算法模型输出为x(k),k=0,1,…,N-1。
一是信噪比(Signal/Noise Ratio,SNR),它是最常用的指标,其定义为
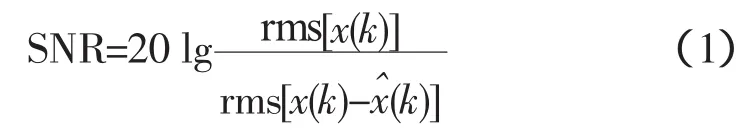
式中,rms表示均方根(root mean square),单位为dB。有些程序中的SNR表达式略有不同。
二是百分比误差Dp,其定义为
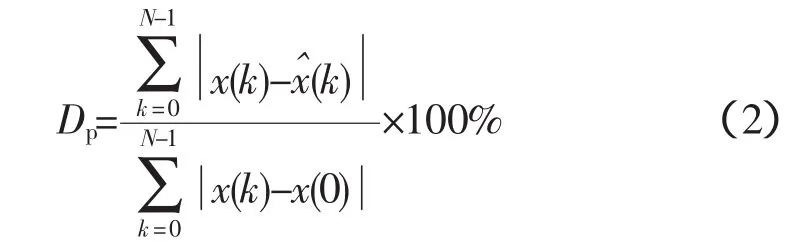
一般认为,百分比误差小于10%以及SNR达到20dB以上时,算法分析得到可以接受的结果,接近40 dB,则更加理想。另外,通过比较真实数据曲线和拟合数据曲线,也可以作为一种辅助手段直观地判断拟合的效果。
当各模态参数都已获得时,即可以重构所辨识信号,与真实采样值进行比较。在同一幅图形中分别描绘出它们的波形,以查看拟合的效果。
2)抗噪声。实际电力系统信号在采样和传输过程中不可避免地受到噪声干扰,故障后系统的响应中更是会有许多杂散的频率分量。因此算法对噪声的敏感性应该比较低,算法本身最好具有一定的滤波效果。
3)快速性。为了达到在线实时或者准实时辨识的目的,对算法的耗时有较高的要求。实际工程中,采用哪种算法,很大程度上受算法时间性限制。
4)分辨率。辨识算法多种多样,辨识结果往往是一系列的频率分量。实际采用的算法应能够在这一系列频率分量中准确地找到所关心的系统主导振荡模式。
5)稳定性。辨识算法应具有算法稳定性,实际应用中是循环辨识过程,算法可能需要复用历史数据,这时要求算法在做长时间计算过程中不会受到误差积累等因素的影响。
3.2 辨识模型定阶
模型阶数P的确定是辨识算法的重要问题,但实际大型互联电力系统动态过程中,系统阶数是未知的,并且是高维的,用于拟合的模型都只能是一个降阶的近似模型。但是需要指出的是,通常我们最关心的是系统低频振荡的主导模式,并不要求获得所有的振荡模式。
本文提出一种辨识自适应定阶方法,首先取定一个初始定阶分辨率,然后进行信号辨识,最后通过判断Dp、SNR等指标是否满足预设要求,满足则输出结果,否则调整定阶分辨率,继续求解,整个计算流程如图3所示。
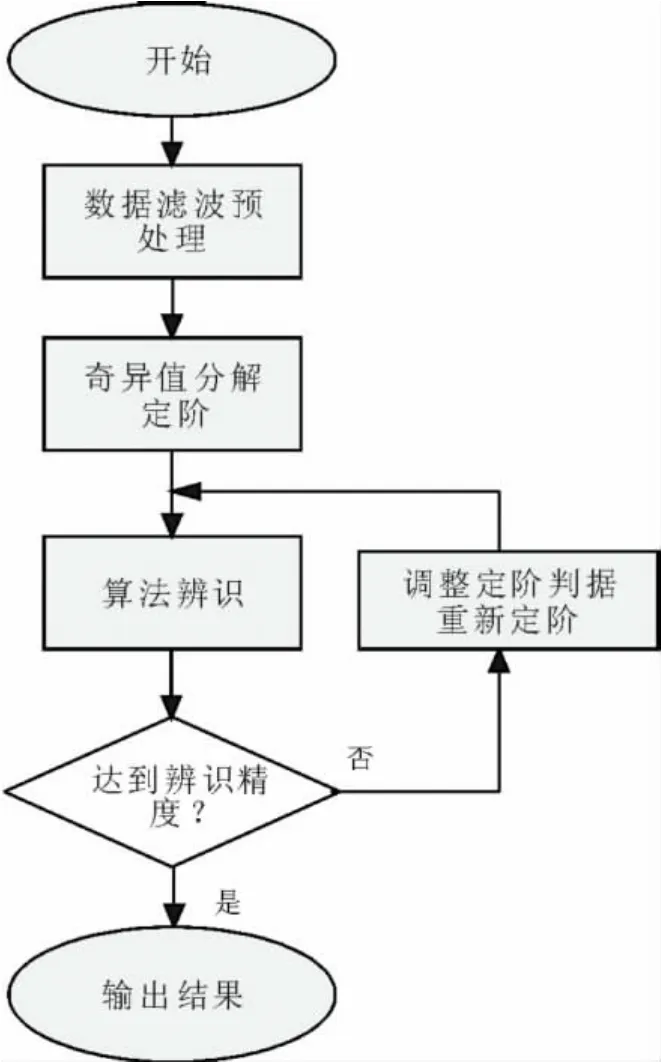
图3 自适应定阶算法的原理框图
4 算例分析
文献[5]中的四机两区域系统是一个典型的包含区域间振荡模式和区域内振荡模式的测试系统。其潮流分布见图4。

图4 四机两区域交直流系统
首先利用PSS/E自带的小信号分析工具LSYSAN,对该系统进行小扰动分析,结果见表1。
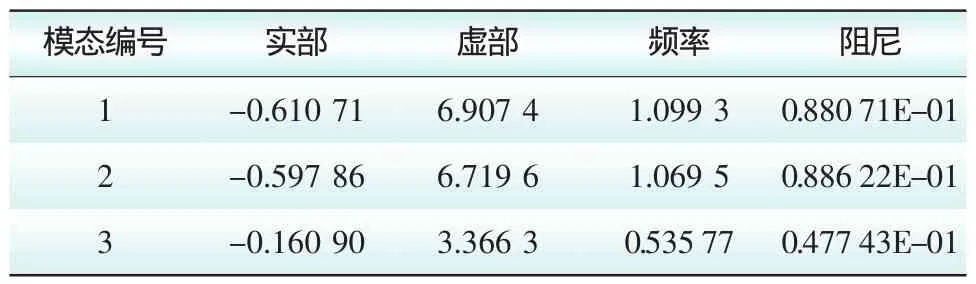
表1 四机两区域系统的特征值分析结果
由分析结果可见,该系统存在3个振荡模式,其中1、2两个模式振荡频率在1 Hz左右,是区域内振荡模式,模式3振荡频率是0.536 Hz,为典型的区域间振荡模式。同时,3个振荡模式的阻尼都小于10%,系统阻尼不足。
其次,利用PSS/E的时域仿真功能获取系统小扰动下的动态响应曲线。需要特别注意施加的扰动必须足够小,其标准是系统仍然在初始平衡点附近工作。否则在大扰动下系统已经偏离初始稳定运行点,那么以线性化的方法套用到非线性系统,势必得不到准确的结果。因此在这里采用微调系统负荷的方法获得系统的线性化响应,具体为调整母线7上的负荷5 MW[23-25],仿真结果见图5。

图5 发电机1的转速偏差
观察图5后,截取扰动后的振荡线性化部分,即6.5 ~10 s之间的部分进行辨识,模态辨识的结果以及相关的辨识评价指标如表2所示,重构分析结果见图6、图7。注意这里仅列出了区域间振荡模式的辨识结果(以下的讨论中也相同)。
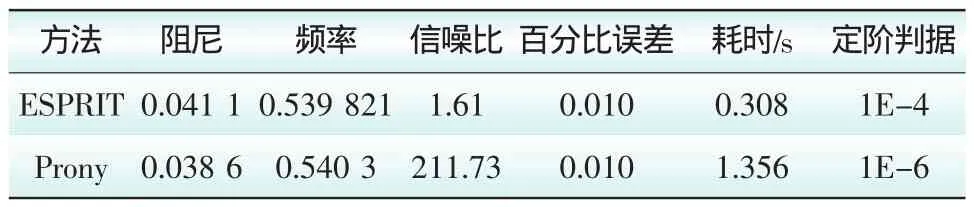
表2 四机两区域系统的小信号分析结果
接着对7 ~8支路上传输的有功功率分别利用两种方法进行辨识,所得的结果如图8所示。
模态辨识的结果以及相关的辨识评价指标如表3所示,重构分析结果见图9、图10。
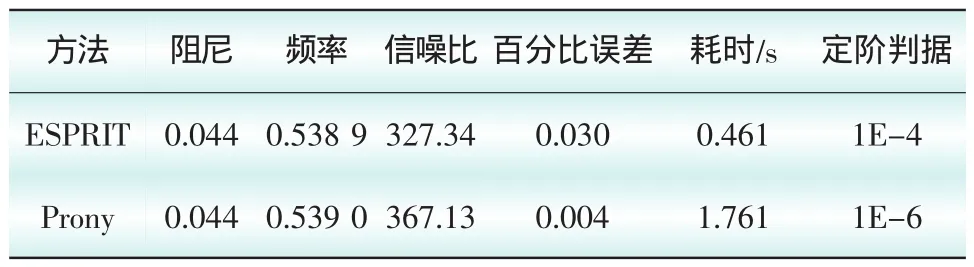
表3 四机两区域系统的小信号分析结果
接下来取1号和3号发电机之间功角差为辨识对象,其形如图11所示。

图6 ESPRIT方法的重构图形比较
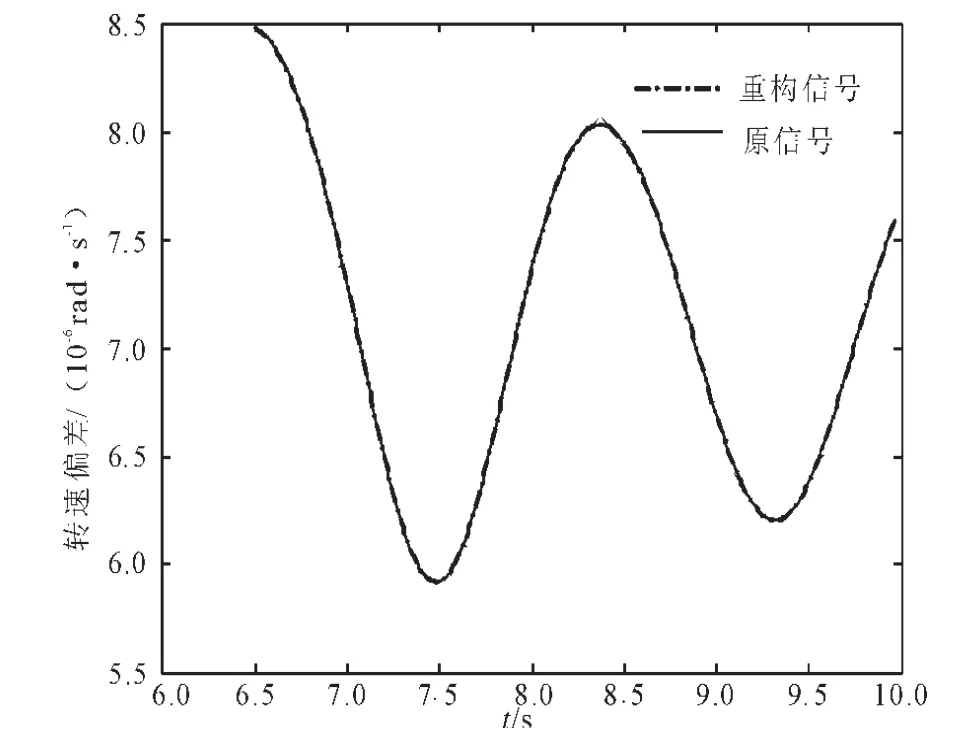
图7 Prony方法的重构图形比较

图8 7 ~8支路功率
模态辨识的结果以及相关的辨识评价指标如表4所示,重构和结果见图12、图13。

表4 四机两区域系统的小信号分析结果

图9 ESPRIT方法的重构图形比较
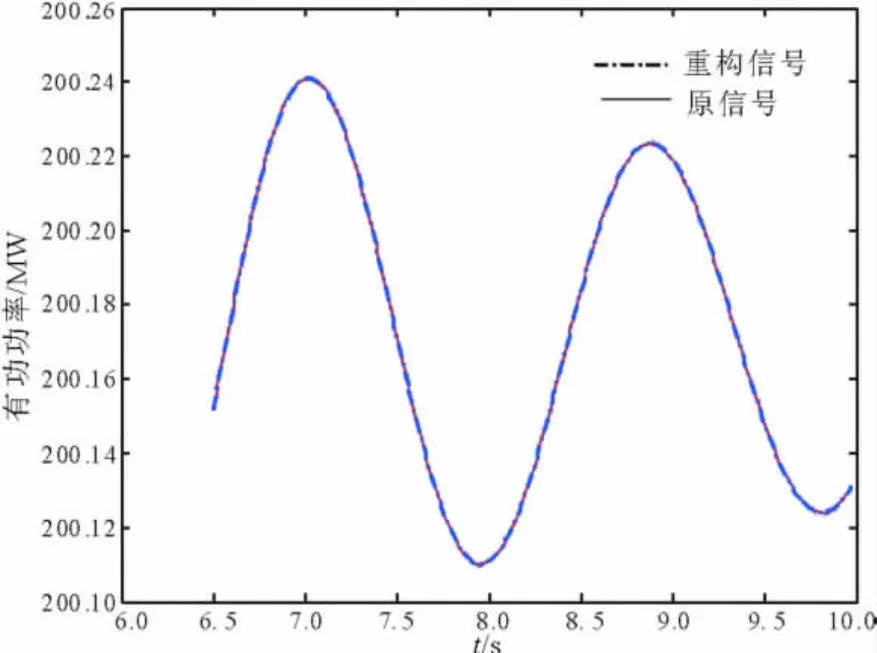
图10 Prony方法的重构图形比较

图11 发电机1,3的功角差
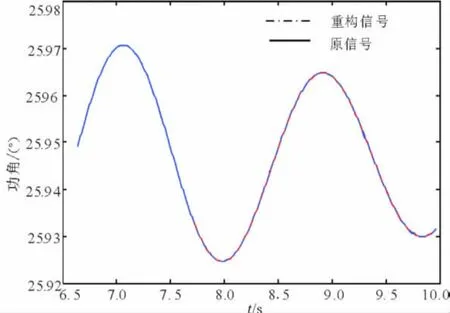
图12 ESPRIT方法的重构图形比较

图13 Prony方法的重构图形比较
经上述算例验证,可见Prony方法和ESPRIT方法均能很好地实现辨识,在选择适当的定阶判据后,百分比误差均小于5%。同时两种方法进行在线辨识的耗时均不超过2 s,这对于在线发现和判定动态失稳有重要的意义,有利于后续补救控制的实施。
5 结论
本文围绕电力系统低频振荡监控系统的组成结构展开研究。第一个核心内容是提出了从监测到控制的双层体系结构。其次针对监测时需要用到的模式辨识方法做了研讨,分析比较了不同辨识方法的优劣,重点比较了Prony和ESPRIT两种方法。从在线辨识算法的工程要求出发讨论了辨识窗长度、噪声影响等关键问题,在分析重构定阶标准对重构精度的基础上提出一种适用于Prony以及ESPRIT方法的电力系统低频振荡实时监测定阶算法。得出的主要结论如下:
1)在线辨识算法应用时,取不同长度的数据段计算复杂度显然不同,耗时也有明显的区别。过长的辨识窗可能引入更多的噪声,给辨识算法定阶带来困难。
2)通过对不同信号的算例检验发现,相对功角信号作为辨识对象往往可以大大缩减定阶数,定性地看,功角信号和转速信号更直接地反映了发电机的动态过程,信号本身受噪声影响较小。
[1] 刘振亚.加快建设坚强国家电网促进中国能源可持续发展[J].中国电力,2006,39(9):1-3.
[2] 李丹,苏为民,张晶,等.“9.1”内蒙古西部电网振荡的仿真研究[J].电网技术,2006,30(6):41-47.
[3] 余贻鑫,李鹏.大区电网弱互联对互联系统阻尼和动态稳定性的影响[J].中国电机工程学报,2005,25(1):6-11.
[4] 蔡洋.电网调度管理须与电网发展俱进—北美东北电网事故浅析[J].电网技术,2004,28(8):6-10.
[5] K UND UR P.Power System Stability and Control[M].New York:McGraw-Hill Inc,1994.
[6] 王克英,穆钢,陈学允.计及PMU的状态估计精度分析及配置研究[J].中国电机工程学报,2001,21(8):29-33.
[7] 李丹,韩福坤,肖晋宇,等.华北电网广域实时监测系统[J].电网技术,2004,28(23):52-56.
[8] 胡志祥,谢小荣,肖晋宇,等.广域测量系统的延迟分析及测试[J].电力系统自动化,2004,28(15):39-43.
[9] GRIGSBY L L.The Electric Power Engineering Handbook[M].Cleveland:CRC Press,2000.
[10] 卢强.南方电网的灾变防治体系——南方电网的Super EMS[J].电力系统自动化,2005,29(24):1-2.
[11] KORBA P,LARSSON M,REHTANZ C.Detection of Oscillations in Power Systems Using Kalman Filtering Techniques[C].IEEE Conference on Control Applications,2003.CCA 2003.Turkey:Istanbul,CCA 2003(1):183-188.
[12] ZHANG Xiaoping,CHRISTIAN Rehtanz,BIKASH Pal.Flexible ACTransmission SystemsModelingand Control[M].New York:Springer,2006.
[13] HAUER J F,DEMEURE C J,Scharf L L.Initial result in Prony Analysis of Power System Response Signals[J].IEEE Transactions on power system,1990,5(1):80-89.
[14] OVERSCHEE P,MOOR B D.Subspace Identification for Linear Systems:Theory,Implementation,Applicalions[M].Boston:Kluwer AcademicPublishers,1996.
[15] TAKASHIHiyama,NAOTOSuzuki,TAKAHIKOFunakoshi.Online Identification of Power System Oscillation Modes by Using Real Time FFT[J].IEEE Power Engineering Society Winter Meeting,2000,2(1):1521-1526.
[16] 张贤达.现代信号处理[M].北京:清华大学出版社,2000.
[17] 张静,徐政,王峰,等.TLS-ESPRIT在低频振荡分析中的应用[J].电力系统自动化2007,31(20):84-88.
[18] DIMITRIS G,VINAY K INGLE,STEPHEN M,et al.Statistical and Adaptive Signal Processing[M].London,Artech House Press,2005.
[19] BOLLEN M H J,STYVAKTAKIS E,IRENE G,et al.Categorization and Analysis of Power System Transients.IEEE Transactions on Power Delivery[J].2005,20(3):2298-2306.
[20] 芦晶晶,郭剑,田芳,等.基于Prony方法的电力系统振荡模式分析及PSS参数设计[J].电网技术,2004,28(15):31-34.
[21] 刘红超,李兴源.基于Prony辨识的交直流并联输电系统直流阻尼控制的研究[J].中国电机工程学报,2002,22(7):54-57.
[22] 鞠平,谢欢,孟远景,等.基于广域测量信息在线辨识低频振荡[J].中国电机工程学报,2005,25(22):56-60.
[23] 肖晋宇,谢小荣,胡志祥,等.电力系统低频振荡在线辨识的改进Prony算法[J].清华大学学报:自然科学版,2004,44(7):883-887.
[24] 姚李孝,宁卜,沈东方,等.异步运行状态下振荡中心研究[J].电网与清洁能源,2008,24(12):16-20.
[25] 李鹏,徐光虎,刘春晓,等.从时频角度重新审视南方电网的区间功率振荡[J].南方电网技术,2010,4(1):6-10.

