基于行程时间可靠性的弹性需求SUE配流模型

吴开信，牟瑞芳

(西南交通大学 交通运输与物流学院，四川 成都 610031)

交通网络可靠性最早由 Asakura Y 和 Kashiwadani M 于 1991年提出[1]，其后各国学者从不同侧面对其进行了研究，其中，行程时间可靠性一直是研究的热点。行程时间和行程时间可靠性不仅是用户关心的路网性能评价指标，也是交通规划和管理部门为用户提供服务的质量评价指标。对于用户，希望在一定的出行时间范围内到达目的地；作为管理者，希望提供更多可靠的服务，使用户出行时间波动性较小[2]。OD (origin-destination) 需求量会受到网络运营状况的影响。当网络中两个节点之间的拥挤程度增加时，部分用户可能会因广义出行费用的增加而改变自己的出行目的地或放弃出行；当通过投资使路段通行能力提高，OD 需求量也会明显改变。为了精确描述出行者和路网状况之间的交互作用，引入弹性需求表示用户的路径选择行为将更加符合实际。为此提出基于行程时间可靠性的弹性需求随机用户平衡 (Stochastic User Equilibrium，SUE) 配流模型，给出与其等价的变分不等式形式，并分析相应的算法。

1 行程时间可靠性和广义出行费用

1.1 路段行程时间和路径行程时间

交通网络G＝(N,A)，N为网络中的节点集合，A为网络中的路段集合。W为 OD 对集合，w为W中的一个元素，Pw为所有有效路径集合。假设路段a的设计容量为，通行能力是一个非负的连续随机变量，而且服从于区间[]上的均匀分布，ρa表示路段a由于突发交通事故、自然灾害等原因而造成的实际容量下降程度，ρa∈[0,1)。路段上的实际行程时间会随路段通行能力的变化而变化，因而也是一个随机变量，在此采用 BPR (Bureau of Public Roads) 函数确定路段上的实际行程时间：

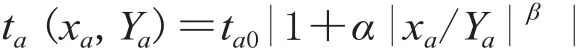
式中：ta、ta0、xa和xa/Ya分别表示路段a上的实际行程时间、自由行程时间、交通流量和饱和度；α和β为 BPR 函数中的确定性参数，可从统计资料中获得。假设路段通行能力的随机变化独立于路段上的交通流量，可以求得路段a上的行程时间均值[3]：

当交叉口的延误忽略时，路径行程时间Tkz是由组成路径的各路段行程时间ta决定的，即

式中：表示路段a和路径k的关联系数，如果a∈k，则＝1；否则，＝0。根据中心极限定理，可知Tk服从正态分布，并且有：

1.2 路段行程时间可靠性和广义出行费用

定义路段行程时间可靠性为出行者在某一路段上完成一次出行所需时间在规定时间范围内的概率。

路段时间可靠性用数学表达式表示为：ra＝P(ta≤ta0＋Δa)，即实际行程时间小于自由行程时间加上出行者可接受延误 Δa的概率。显然，路段不同，Δa的值也会不同，可根据统计资料进行确定。

出行者在选择路径时一般需考虑两个指标：行程时间和行程时间可靠性。这两个指标具有以下 3个特点。

（1）不可公度性，即量纲不同，不便于相互之间进行运算。

（2）变化范围不同。

（3）矛盾性，即一种方案能使某个指标值得到改善，但可能以另一个指标值的变坏为代价。

根据出行者对行程时间和行程时间可靠性所持的不同态度，定义出行者在路段a上的广义出行费用：

式中：αa为路段a上的行程时间费用系数，表示将行程时间转换成相应的出行费用；βa为路段a上的行程时间可靠性费用系数，表示将行程时间的不可靠性转换成相应的出行费用。

由此，确定了一个综合意义上的具有相同量纲的阻抗值。费用系数αa和βa分别反映出行者对行程时间和行程时间可靠性的态度。αa越大、βa越小则出行者越倾向于以行程时间作为择路标准；反之，则越倾向于以行程时间可靠性作为择路标准。在此规定：路段上的广义出行费用是该路段交通流量的严格增函数，即 dca/dxa＞0，∀a∈A；路段上的广义出行费用只与组成该路段的交通流量有关，与其他路段的交通流量无关，即 dca/dxb＝0，∀a、b∈A，a≠b。由路径和路段之间的相互关系，出行者在路径k上的广义出行费用为所包含路段的广义出行费用之和，即

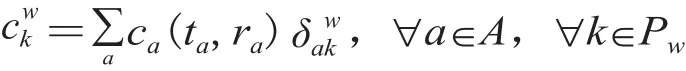
2 基于行程时间可靠性的弹性需求SUE模型

2.1 建立模型

研究行程时间可靠性应考虑出行者的路径选择行为，目前国内外学者对行程时间可靠性的研究大多是基于 Logit 模型或 Probit 模型。Chen 等考虑了出行者对行程时间的意识误差和行程时间本身的随机性，将用户选择进行了分类，利用 Monte Carlo 技术，计算了不同路径选择模型下的行程时间可靠性[4]。Lam 等通过交通流模拟仿真估计行程时间可靠性[5]。通过比较可知，Logit 模型简单易于理解，因此研究采用此模型评价行程时间可靠性。对研究的有关假设如下。

（1）路径k上的交通流量满足 Logit 模型：

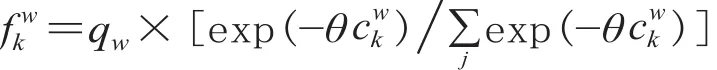
式中：随机变量与路径行程时间及其可靠性有关；qw表示第w个 OD 对之间的交通需求量；θ是一个非负系数，可理解为出行者对路网的熟悉程度，θ越大，说明出行者对出行费用的认识越准确，估计的阻抗方差越小。

（2）Sw(cw) 是关于cw的凹函数。Sw(cw) 和cw分别表示第w个 OD 对之间的期望最小估计广义出行费用和广义出行费用。由定义可知：

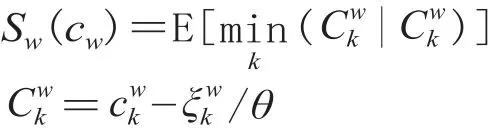
式中：表示估计路径出行费用；为服从 Gumbel 分布的随机变量。

一般情况下，OD 矩阵随广义出行费用矩阵的变化而变化，为了更好地描述需求量的可变性和用户选择行为的随机性，现假设qw是Sw(cw) 的连续单调下降函数，并有上确界Qw，即

在实际运用中，需求函数可采用线性形式[5]：

式中：表示路网处于理想状态时第w个 OD 对之间最大交通量；常数ψ表示需求量对期望最小估计广义出行费用的灵敏度。

基于行程时间可靠性的弹性需求SUE配流问题可用以下数学规划模型表示：

模型中为第w个 OD 对之间交通量需求函数的反函数。

2.2 解的惟一性与等价性证明

2.2.1 惟一性证明

将约束条件⑵代入目标函数⑴，可得：

此时，目标函数的第三项是xa的严格凸函数，但相对于路径流量来说是凸函数，其余3项是关于的严格凸函数。因此，目标函数是关于的严格凸函数，又由于约束条件都是线性的，此数学规划模型有惟一最优解。

2.2.2 等价性证明

构造模型⑴的Lagrange 函数：

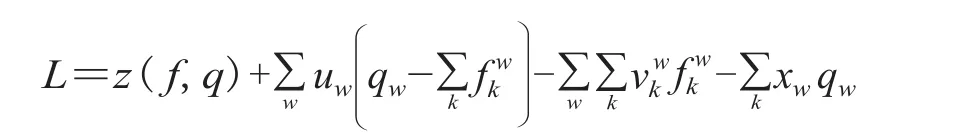
由于此数学规划模型是一个凸规划模型，因此有惟一的路径流量最优解，并且 K-T 条件是惟一解的充分必要条件。K-T 条件如下。

式中：uw、和xw分别是公式⑵、公式⑷和公式⑸的 Lagrange 算子。

设Pw是第w个 OD 对之间所有有效路径集合，即＞0，∀k∈Pw，从而有＝0，此时由公式⑹可得：

说明路径k上流量的最优解满足 SUE 平衡条件。当qw＞0时，xw＝0，此时由公式⑺可得：

由于exp[−(qw)]＝()，因此，qw＝。此式是弹性需求函数关系式的具体表达式。

2.3 变分不等式模型

在城市交通网络G＝(N，A) 中，假设uw表示第w个 OD 对之间最小出行费用。对于 ∀k∈Pw，当＞0 时，uw－＝0；当＝0 时，uw－≤0，则称路径流量为平衡流[6]。

变分不等式模型：

根据文献[7]的结论，如果变分不等式⑼有解，则必然存在Lagrange算子uw、和xw，使得：

3 弹性需求 SUE 模型的算法

模型的具体求解步骤如下。

步骤 1：确定有效路径集合。

步骤 2：初始化。在没有交通量的情形下，算出有效路径的广义出行费用(0) 及期望最小估计广义出行费用，利用交通量需求函数得到相应的交通流量，基于(0) 和进行随机分配，计算初始路段流量{xa,1}和有效路径流量{}，令n＝1。

步骤 3：令ta,n＝ta(xa,n)，根据当前路段流量{xa,n}和有效路径流量{}计算出路段广义出行费用ca,n、有效路径广义出行费(n)和，再由交通量需求函数得出新的交通量，并对在网络上进行重新分配，得出新的有效路径流量{}。

步骤 5：收敛性检验。收敛准则：(－)/＜ε，∀w∈W。当误差ε达到预定误差时，结束循环；否则，令n＝n＋1，转回步骤 3。

4 结束语

基于出行者根据行程时间和行程时间可靠性选择路径，路径上的交通流量满足 Logit 模型，建立弹性需求交通网络 SUE 配流模型，并给出与其等价的变分不等式形式，提出相关模型的算法。模型假定路段之间是相互独立的，但是在实际路网中，路段上的广义出行费用是相互影响的。下一步研究的方向是在路段之间相互影响的情况下，进行出行时间可靠性分析和平衡配流，以及基于时间可靠性的弹性需求交通网络平衡配流问题的灵敏度分析，并在交通网络上进行测试。

[1] Asakura Y，Kashiwadani M.. Road network reliability caused by daily fluctuation of traffic flow[C]// Proceedings of the 19th PTRC Summer Annual Meeting. Brighton，1991：73-84.

[2] 许 良，高自友. 基于出行时间可靠性的城市交通网络设计[J]. 系统仿真学报，2008，20(2)：494-498.

[3] Lo H.K.，Tung Y.K.. Network with degradable links：capacity analysis and design[J]. Transportation Research Part B，2003，37(4)：345-363.

[4] Chen A.，Yang H.，Lo H.K.，et al. Capacity Reliability of a Road Network：An Assessment Methodology and Numerical Results [J]. Transportation Research Part B，2002，36(3)：225-252.

[5] Lam W.H.K.，Xu G.. A traffic flow simulator for network reliability assessment[J]. Journal of Advanced Transportation，1999，33(2)：159-182.

[6] Ben-Akiva M.，Leman S.R..Discrete choice analysis：Theory and application to travel demand [M]. Cambridge，MA：M IT Press，1985.

[7] 高自友. 城市交通连续平衡网络设计：理论与方法[M]. 北京：中国铁道出版社，2000.