均匀球扭矩德拜级数分析

李仁先，韩香娥，帕尔哈提江·吐尔孙

（西安电子科技大学理学院，陕西西安710071）

均匀球扭矩德拜级数分析

李仁先，韩香娥，帕尔哈提江·吐尔孙

（西安电子科技大学理学院，陕西西安710071）

基于会聚光束所产生的扭矩来实现对小粒子的操纵已在物理学、生物学等领域得到了广泛的应用。为了分离出单个散射过程对扭矩的贡献，给出扭矩物理机理的解释，本文引入德拜级数分析了高斯波束对均匀球粒子所产生的扭矩。计算表明，当德拜项p从1取到一个足够大的值后，德拜级数计算结果与广义米氏理论结果吻合。文中重点分析了单阶p散射过程对横向扭矩的贡献，结果表明：当线极化光束入射时，p=1～5散射过程都可以产生横向扭矩，但扭矩的方向不同；当圆极化光束入射时，p=-1和0对应的扭矩远大于p=1～4对应的扭矩，且p=0过程产生与其他p过程相反方向的扭矩。

辐射扭矩；德拜级数；高斯光束；光钳；角矩

1 Introduction

It is well known that transfer of angular momentum from a laser beam to a particle can produce radiation torques，which can be employed to the manipulation of microscopic objects[1］，and it have been widely used in the fields of biology，physics，optofluidics，etc.The torque may be caused by circularly polarized plane wave，which carries spin angular momentum[2，3］.In this case，the particle needs to be absorbing.The torque may also occur in the case of a sphere illuminated by an off-axis shaped beam[4］.In this case，the off-axis beam has orbit angular momentum.It is obvious that when an absorbing particle is illuminated by an off-axis circularly polarized focused beam，both the spin angular momentum and the orbit one will be transferred from the beam to the particle.

Many researchers have been devoted to the theroretical prediction of radiation torque，and different approaches have been developed.When the size of particle is much larger than the wavelength of incident beam，i.e.d＞10λ（d is the diameter of the particle and λ is the wavelength），the geometrical optics can be employed to the prediction of radiation torque[5］.Conversely，the Rayleigh model[6］can be employed to the prediction of radiation torque exerted on a particle which is much small than the wavelength，i.e.d≪λ.Both geometical optics and Rayleigh model are approximate approaches.The two limiting cases can be unified by the rigorous theory“Generalized Lorenz-Mie Theory（GLMT）”[7，8］，which is the solution to the Maxwell′s equations and is suitable for any d/λ.

GLMT is a rigorous electromagnetic theory，and can exactly predict the radiation torque exerted on a sphere.However，the solution is complicated combinations of Bessel fuctions， and its mathematical complexity obscures the physical interpretation of various features of radiation torque.Of all electromagnetic theories，the Debye Series Expansion（DSE），which is a rigorous theory，expresses the Mie scattering coefficients into a series of Fresnel coefficients and gives physical interpretation of different scattering mode.The DSE is an efficient tool to make explicit the physical interpretation of various features of radiation torque which are implicit in the GLMT. The DSE is firstly presented by Debye in 1908 for the interaction between electromagnetic waves and cylinders[9］.Since then，the DSE for electromagnetic scattering by homogeneous[10］，coated[11］，multilayered spheres[12］，multilayered cylinders at normal incidence[13］，homogeneous[14］，multilayered cylinder at oblique incidence[15］， and spherical gratings[16］are studied.In our previous work，the DSE is employed to the theoretical research on the radiation pressure force exerted on a homogeneous[17］and multilayered spherical particle[18］. However， the DSE is，in our knowledge，not employed to the research on radiation torque.This paper is devoted to the theoretical prediction of adiation torque exerted on a sphere using DSE.

2 Theoretical background

We consider a sphere whose radius is a and refractive index is m1embedded in the dielectric medium of refractive index m2.The sphere is characterized by a size parameter of 2πa/λ，where λ is the wavelength of the incident wave in the surrounding free space.The center of the sphere is located at OPwhich is the center of the Cartesian coordinate system OPχyz.It is illuminated by a Gaussian beam whose center of beam waist is located at OG，which is the center of the Cartesian coordinate system OGuvw，with OGuparallel to OPχand similarly for others.The coordinates of OGin the system OPχyzare（χ0，y0，z0）.The time dependent term of incident beam is exp（iωt）with ω being the angular frequency and will be omitted from all formulas.

The longitudinal radiation torque Tzand the two transverse radiation torques Tχand Tyare given respectively by

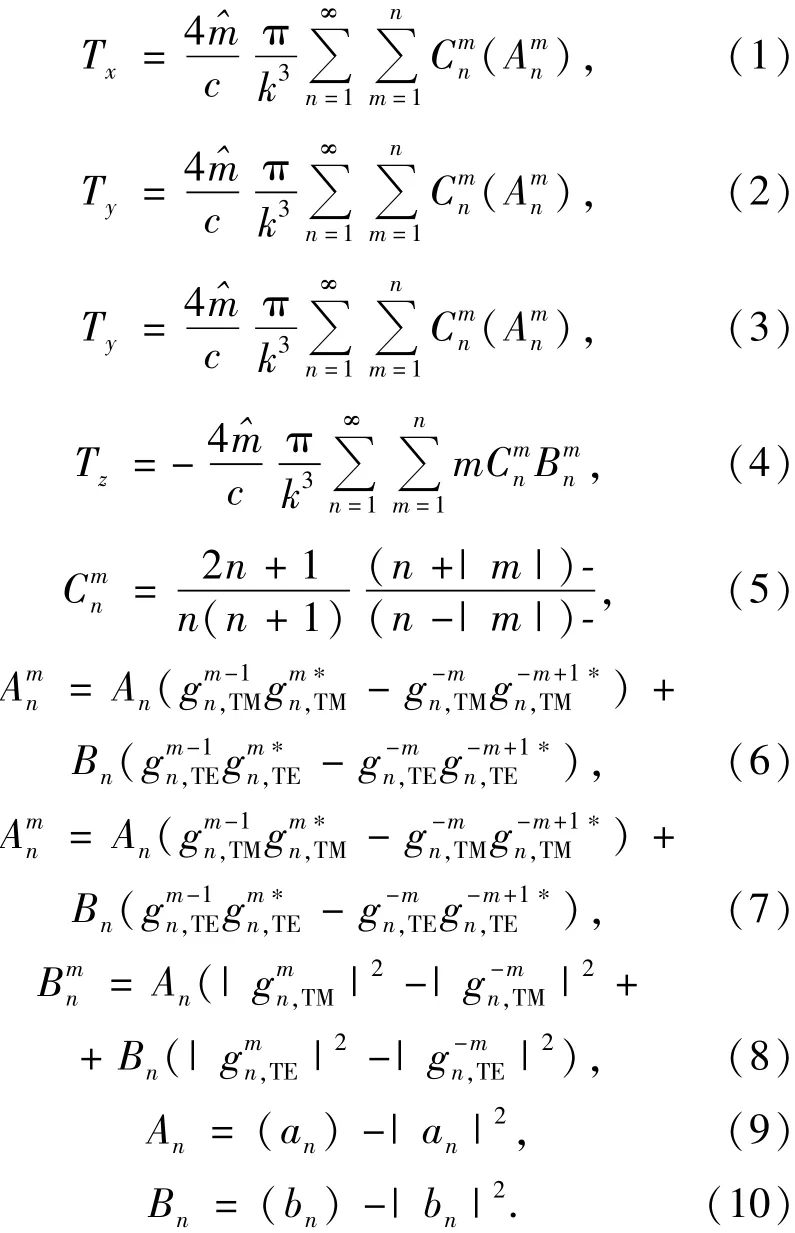
In Eqs.（1）-（3），the prefactor P/（），in which P is the power of the beam，is omitted. The star denotes complex conjugation.Theandare so-called Beam Shaped Coefficients（BSCs），and their expression in Bessel function can be obtained by the integrated localized approximation.For first-order Davis model，BSCs can be simply expressed by

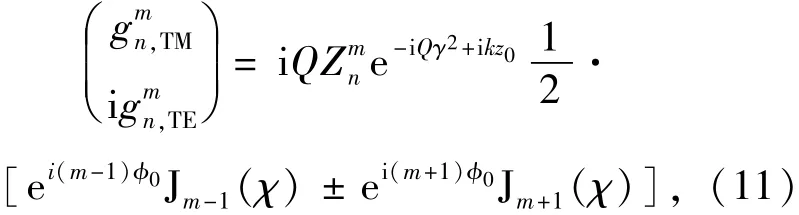
with

where ω0is the beam-waist radius and Jm（χ）is the Bessel function of first kind.

For on-axis illumination（χ0=y0=0），BCSsandreduce to a single set gn，which can be calculated by using the Localized Approximation（LA）

Note that we can obtain the radiation torque induced by other shaped beams by replacing the corresponding BCSs in Eqs.（11）-（17）.

The anand bnin Eqs.（1）-（10）are traditional Mie scattering coefficients，and can be expanded using Debye series as[12］

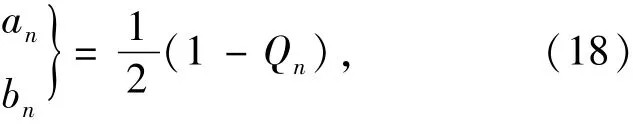
with

or

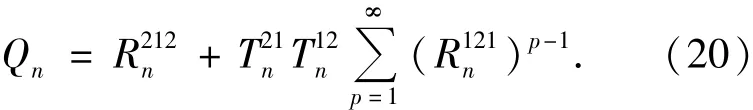
Where p is the mode of refraction.andrepresent respectively the portions of transmission of wave from region 2 to region 1 and from region 1 to region 2.andrepresent respectively the portions of reflection on the surface of region 2 to region 1 and of region 1 to region 2.They are defined by

The prime indicates the derivative of the function with respect to its argument.The（z）and（z）are respectively spherical Ricatti-Hankel functions of first and second kinds

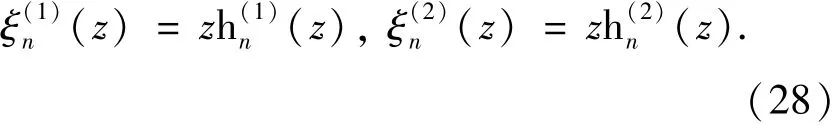
When summed over n，the first term 1/2 in Eq.（18）corresponds to the diffraction and the second termto the reflection ray.The third term is a series which describes the contribution of all modes of refraction.Each term in the series represents the contribution of that mode which undergone（p-1）internal reflections，and then emerged from the sphere.We can then choose one or several terms in the series to study their contributions and their characteristics.

3 Results and discussions

In this section，DSE is employed to the analysis of radiation torque exerted on a sphere，and the radiation torque introduced by single Debye mode or multiple modes are mainly analyzed.The cases of both linearly polarized beam incidence and circularly polarized one are considered.During simulation，we assume the particle is a hard polystyrene[19］with radius of 1.0 μm surrounded by air（m2=1.0）.The wavelength of incident beam is 0.785 μm，and the beam-waist radius is 1.0 μm.

3.1 Linearly polarized beam incidence

We firstly consider the case of linearly polarized beam incidence.Here we assume the particle is a absorbing polystyrene with refractive index of 1.573 -6.0×10-4i.When the whole summation over p in Eq.（20）from 1 to∞，the GLMT results are recovered.In fact，when p ranges from 1 to a value pmaxlarge enough，the results obtained by DSE is identical to that by GLMT.Our results are firstly compared with that by GLMT with pmaxas parameters.In Fig.1，we depict the transverse radiation torque Tyversus χ0with pmaxranges from 15 to 100. It is shown in Fig.1 that when pmax=15，the results is very close to that by GLMT，while when pmax= 100，the results is same to that by GLMT.Here pmax=-1 and pmax=0 represent the diffraction and direct reflection，respectively.

Fig.1 Transverse radiation torque Tyvs χ0for linearly polarized beam incidence（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573-6.0×10-4i.）

We can find from Fig.1 that the torque for pmax=15 is larger than that for pmax=100 and pmax= 50，while the torque for pmax=20 is smaller than that for pmax=100 and pmax=50.For explanation of such phenomena，it is necessary to isolate the contribution of single scattering process to the total torque.

Now we consider the contribution of single pmode to radiation torque.Figs.2 and 3 give the transverse radiation torque Tyversus χ0of single mode with mode p as parameters.From Figs.2 and 3，we can find that all scattering processes for p= -1-5 can produce transverse radiation torque，and while the directions of torque are different.For example，the torques for p=-1 and p=3 is opposite to that for others.This can be easily expained by using geometrical optics.It can also find that the torques for p=-1，0 and 1 are much larger than that for other modes.This is caused by the decreasing of energe with the increasing of interaction between waves and particles.

Fig.2 Transverse radiation torque Tyversus χ0（p= -1，0，1）（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573-6.0×10-4i.）

Fig.3 Transverse radiation torque Tyversus χ0（p= 2-5）（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573-6.0×10-4i.）

3.2 Circularly polarized beam incidence

In this section，we focus on the case of circularly polarized beam incidence.During simulation，we assume the particle is a transparen polystyrene with refractive index of 1.573.

Similarly，we first depict the transverse radiation torque Tyversus χ0with parameters pmax（see Fig.4）.From Fig.4，we can firstly find that when pmaxis larger enough，the GLMT results are recovered.It is shown in Fig.4 that the torque for pmax= 50 is larger than those for pmax=15，20 or 100.

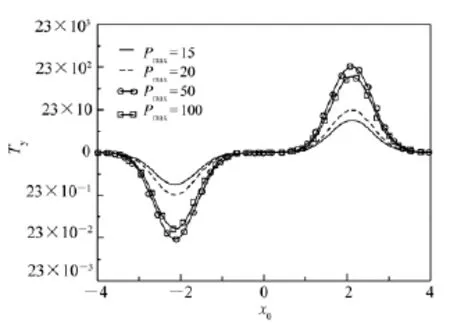
Fig.4 Transverse radiation torque Tyvs χ0for circularly polarized beam incidence（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573）

Fig.5 Transverse radiation torque Tyversus χ0（p= -1，0）（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573）

In order to obtain the physical explanation of radiation torque，we calculate the radiation torque corresponding to single scattering process，namely single Debye mode p.It is depicted in Figs.5 and 6 for the radiation torque with parameters Debye mode p.From Figs.5 and 6，we can find that the torques for p=-1 and 0 are much larger than those for p= 1-4.This can be explained in the same way with that for linearly polarized beam incidence.We can also find that the direction of torque for p=0 is opposite with that for other mode p.This can also be explained using geometrical optics.

Fig.6 Transverse radiation torque Tyversus χ0（p= 1-4）（a=1.0 μm，λ=0.785 μm，w0=1.0 μm，m1=1.573-6.0×10-4i.）

4 Conclusions

DSE is introduced to study of radiation torque exerted on a homogeneous sphere，and it allows the analysis of contribution of single scattering process to full radiation torque，and gives the physical mechanism of radiation torque.The analysis of radiation torque corresponding to single Debye mode p or multiple modes is of great importance to the improvement of optical manipulation.

Reference：

[1］ASHKIN A，DZIEDZIC J M.Optical trapping and manipulation of viruses and bacteria[J］.Science，1987，235：1517-1520.

[2］FRIESE M E J，NIEMINEN T A，HECKENBERG N R，et al..Optical alignment and spinning of laser-trapped microscopic particles[J］.Nature，1998，394：348-350.

[3］STEWART A M.Angular momentum of the electromagnetic field：the plane wave paradox resolved[J］.Eur.J.Phys.，2005，26：635-641.

[4］CHANG S，LEE S S.Optical torque exerted on a homogeneous sphere levitated in the circularly polarized fundamentalmode laser beam[J］.J.Opt.Soc.Am.B，1985，2：1853-1860.

[5］GAUTHIER R.C.Trapping model for the low index ring shaped micro-object in a focused lowest order Gaussian beam profile[J］.J.Opt.Soc.Am.B，1997，14（4）：782-789.

[6］ROHRBACH A，STELZER E H K.Optical trapping of dielectric particles in arbitrary fields[J］.J.Opt.Soc.Am.A，2001，18：839-853.

[7］POLAERT H，GREHAN G，GOUESBET G.Forces and torques exerted on a multilayered spherical particle by a focused Gaussian beam[J］.Opt.Commun.，1998，155：169-179.

[8］GOUESBET G，MAHEU B，GREHAN G.Light scattering from a sphere arbitrarily located in a Gaussian beam，using a Bromwich formulation[J］.J.Opt.Soc.Am.A，1988，5：1427-1443.

[9］DEBIJE P.Das elektromagnetische feld um einen zylinder und die theorie des regenbogens[J］.Phys.Z.，1908，9：775-778.

[10］HOVENAC E A，LOCK J A.Assessing the contributions of surface waves and complex rays to far-field scattering by use of the Debye series[J］.J.Opt.Soc.Am.A，1992，9：781-795.

[11］LOCK J A，JAMISON J M，LIN C Y.Rainbow scattering by a coated sphere[J］.Appl.Opt.，1994，33：4677-4690.

[12］LI R，HAN X，JIANG H，et al..Debye series of light scattering by a multi-layered sphere[J］.Appl.Opt.，2006，45：1260-1270.

[13］LI R，HAN X，JIANG H，et al..Debye series of normally incident plane wave scattering by an infinite multi-layered cylinder[J］.Appl.Opt.，2006，45：6255-6262.

[14］LOCK J A，ADLER C L.Debye-series analysis of the first-order rainbow produced in scattering of a diagonally incident plane wave by a circular cylinder[J］.J.Opt.Soc.Am.A，1997，14：1316-1328.

[15］LI R，HAN X，REN K F.Generalized Debye series expansion of electromagnetic plane wave scattering by an infinite multilayered cylinder at oblique incidence[J］.Phys.Rev.E，2009，79：036602.

[16］LOCK J A.Debye series analysis of scattering of a plane wave by a spherical Bragg grating[J］.Appl.Opt.，2005，44：5594-5603.

[17］LI R，HAN X，REN K F.Debye series analysis of radiation pressure force exerted on a spherical particle[J］.SPIE，2009，7507：750708.

[18］LI R，HAN X，REN K.F.Debye series analysis of radiation pressure force exerted on a multilayered sphere[J］.Appl. Opt.，2010，49：955-963.

[19］XU F，LOCK J A，GOUESBET G，et al..Radiation torque exerted on a spheroid：analytical solution[J］.Phys.Rev.A.，2008，78：013843.

Author′s biography：Li Ren-xian（1980—），Doctor，male，works at School of Science，Xidian Universit，Xi′an，China.His main research interests are electromagnetic（light）scattering and its applications，and laser interaction with matter.E-mail：rxli@mail.xidian.edu.cn

Debye series analysis of radiation torque exerted on a sphere

LI Ren-xian，HAN Xiang-e，PARHATJAN T

（School of Science，Xidian University，Xi′an 710071，China）

The radiation torque induced by a focused laser beam has been widely utilized for the optical manipulation of small particles in various fields such as physics，biology，and optofluidics.To isolate the contribution of each scattering process to the radiation torque and to clarify the physical mechanism of radiation torque，the Debye Series Expand（DSE）is introduced to analysis of the radiation torque exerted on a homogeneous sphere by Gaussian beam.When Debye mode p ranges from 1 to a value pmaxlarge enough，the result obtained by DSE is identical to that by Generalized Lorenz-Mie Theory（GLMT）.Furthermore，the radiation torque corresponding to each Debye mode p is mainly analyzed.Results show that when incident beam is linearly polarized，all scattering processes for p in 1-5 can produce a transverse torque while the directions of torque are different.When the beam is circularly polarized，the torques for p in 1 and 0 are much larger than that for p in 1-4，and the direction of torque for p in 0 is opposite with that for other mode p.

radiation torque；Debye series；Gaussian beam；optical tweezer；angular momentum

2010-08-12；

2010-10-13

O436

A

1674-2915（2011）01-0053-07