通信系统中调制类型自动识别方法分析

白立锋，闫 宁

（中国电子科技集团公司第五十四研究所，河北石家庄050081）

0 引言

随着通信技术的发展，通信信号在很宽的频带上采用各种调制样式，如何有效识别这些信号，在很多领域都是重要的研究课题。调制方式是区别不同通信信号的一个重要特征，对于接收的信号，要想正确地解调，分析收到的信号，必须能够正确地识别信号的调制方式，然后采用相应的解调方法。同时，它是构成基于软件无线电的通用接收机和只能调制解调器的重要技术基础，在多体制通信互联和软件无线电方面也有着十分重要的应用。

1 自动识别方法

1.1 AWGN信道模型

当通信信号x（t）通过高斯白噪声（AWGN）信道后，在接收端接收的信号形式为s（t）=x（t）+n（t），其中n（t）为通过窄带系统后的加性窄带高斯白噪声。如果进行通信信号调制类型的区分，需要在时域和变换域进行处理，提取相应的特征参数，根据各种调制类型的特征参数不同进行区分。

1.2 理论分析

小波变换是时间和频率的局部变换，它能够提供信号局部变化的频域信息，是分析非平稳信号的理想工具，小波变换作为特征提取的工具已经得到广泛的应用。对于不同调制方式的信号，小波变换能够有效地提取信号的瞬时特性，小波系数明显差别能够使得调制识别非常简单。对于已知的数字调制信号s（t），利用Haar小波作为母波，经过小波变换后信号为，在一个符合间隔内，或者在码元相同的相邻码元内是正弦信号，这时没有幅度、频率的变化，信号与时间间隔无关，所以在一个信号周期内为常数，但对于不同码元间，由于可能存在幅度、频率等参数变化，信号的小波变换包络是阶跃信号，此外，当小波函数跨越码元的变化时，就会覆盖信号的相位、频率等变化，分析这些变化，可以识别出不同的调制信号。

1.3 识别过程

只要当接收信号的信噪比达到一定的数值，那么噪声对理想信号的影响不是太大，就满足能够自动识别的基本条件。调制信号的识别处理流程如图1所示。

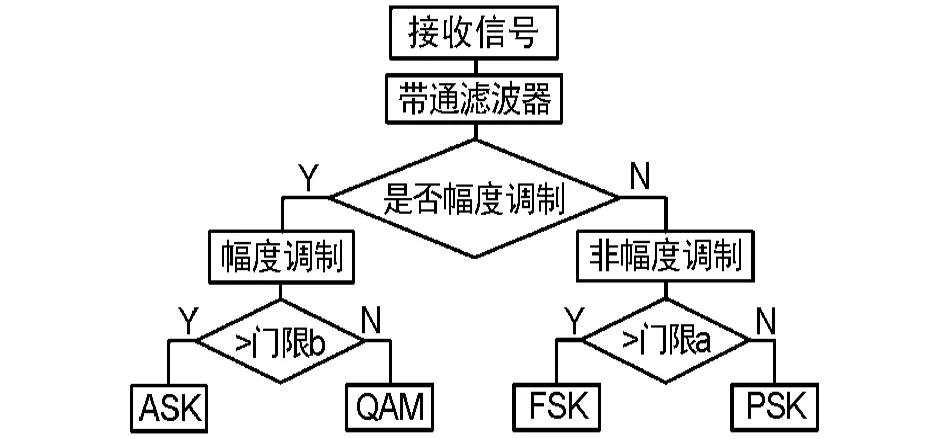
图1 调制识别过程

调制识别过程主要有3部分组成:①接收信号经过带通滤波器以后，通过对特征参数γ的判断是否是幅度方式，基本上就可以把幅度调制和非幅度调制区分开;②在此基础上，如果是幅度调制方式，通过设定的特征参数β区分开（正交幅度调制）QAM和（幅移键控）ASK信号;③如果是非幅度调制方式，通过统计方差的参数S2和参数α将（频移键控）FSK和（相移键控）PSK信号区分开。

1.3.1 幅度调制与非幅度调制

对于接收到的信号，首先决定是否是幅度调制方式，以A（t）表示信号s（t）的瞬时幅度:

式中，Ma为A（i）的均值，将An（i）中心化得到Aan（i）。对于非幅度调制方式的信号Aan（i）应该是一个常数，且约为0，所以定义特征参数为:

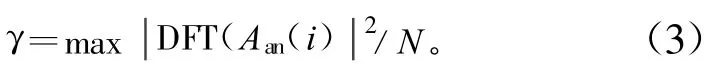
根据以上的分析，通过特征参数γ的不同，将接收的信号初步分为2类:幅度调制信号和非幅度调制信号。

1.3.2 QAM和ASK

ASK信号的幅度只有0和A2种，而QAM至少有3种以上的幅度，所以可以从信号幅度上的差别区分这2种信号。为了去除信道的影响，还需要利用区分幅度调制和非幅度调制的方法将信号瞬时幅度归一化并中心化得到Aan（i）。选择特征参数为归一化并中心化后的幅度均值，定义为:如果信号以等概率出现，可以计算出对于ASK信号β为1，而各种QAM信号β值均为0.3左右，由此可以区分出ASK和QAM信号。

1.3.3 PSK和FSK

对于PSK和FSK信号，可以将接收信号做小波变换，然后再根据特征参数的不同进行处理区分。小波变换作为一种特征提取的工具已得到较广泛的应用，对于不同调制方式下的信号，小波变换能够有效地提取信号的瞬时特性，小波系数的明显差别使得调制信号很容易实现。

对于PSK信号，信号会发生相位的变化，但在一个符号周期内是正弦信号，可以表示为正弦波的形式。在进行处理过程中选择Harr小波作为母波，由于它的小波函数只有2个值，所以它相应的小波变换也很容易应用。PSK信号通过小波变换后，在一个信号周期内为常数，由于得到的函数与相位角度无关，所以在不同信号周期内相位的突变不会引起变换后函数的幅度变换，即PSK信号经过小波变换后得到函数为一个常数。而对于FSK信号，在一个信号周期内经过小波变换后，得到的函数在一个信号周期内为常数，但因为不同周期内，信号的相位不同，而相位的变化使得经过小波变化后的信号为阶跃信号。但当小波函数跨跃信号的不同周期时，就有可能覆盖信号的相位或者频率的变化，使得出现尖峰，也就是说，PSK信号经过小波变化后是一个较低直流电平上带有规律的尖脉冲;而FSK信号经过小波变化后是对阶梯上带有无规律的脉冲，如果相位连续的话波形上将没有尖峰出现。这样将信号经过小波变化、取模，在经过中值滤波器消除波形上的的尖峰，可以得到PSK和FSK信号的小波系数分别为常数和阶跃函数。从而通过选取统计方差α为特征函数就可以将这2种信号区分开。

2 参数的选取

2.1 γ值的选取

参数的选择应该使得识别信号的错误概率最小。对于各种调制方式，特征参数γ的值与信噪比RSN有关，而调制参数是未知的情况下，理论上不能计算出特征参数γ。但是通过数值仿真方法可以得到各种调制信号γ和RSN的关系，通过对比则可根据不同的RSN来确定幅度调制和非幅度调制信号。当RSN≥5dB时，非幅度调制信号的特征参数γ都小于50，而幅度调制信号的特征参数γ都远远大于非幅度调制信号的特征参数，从而可以将γ值设置在30～50之间，根据接收信号信噪比进行具体的调整，就能够准确区分开幅度调制信号和非幅度调制信号。

2.2 β值的选取

参数β的选取与γ选取类似，在不同的RSN下，计算ASK信号和不同的QAM信号的β值的关系如图2所示。从图2中可以看出，QAM调制信号的特征参数β值接近0.3左右。但对于ASK信号，在RSN较大的情况时，特征参数β值接近1，但随着RSN的减小，由于受到二进制信号的影响使得特征参数β值越来越小，所以需要选择合适的β值，以便准确区分ASK信号和QAM信号。综合考虑，即准确区分又能够节省运算量，特征参数β的值选择为0.4为最合适。

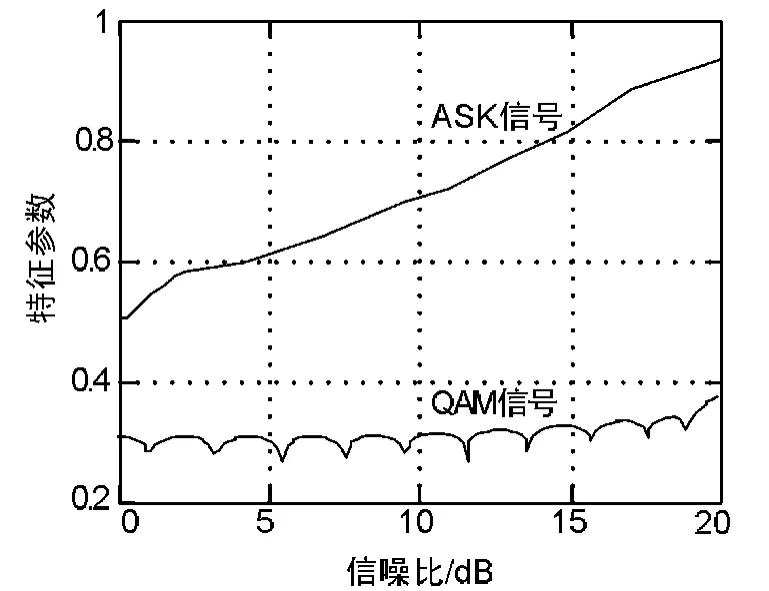
图2 ASK和QAM调制方式特征参数与信噪比关系

2.3 α值的选取

对于方差的参数α的选取，应先计算函数理论方差。由于噪声为加性高斯白噪声，小波系数仍服从高斯分布。用随机变量x表示x服从莱斯分布:

式中，I0为0阶修整贝塞尔函数，σ2为噪声方差;A为没有噪声输入情况下的值。

如果输入信号为FSK时，则由于FSK信号通过中值滤波以后为阶跃函数，理论方差取决于调制参数，无法计算出理论方差。而PSK信号的为带有噪声的常数。当RSN较大时，莱斯分布可以近似为高斯分布。通过中值滤波后，经过简单的变形，参数α选取为:

3 仿真结果分析

应用MARLAB对ASK、PSK、FSK、QAM4种调制方式做仿真分析，母小波选取Haar小波，载波频率选择20kHz的正弦波。符号率为1M/s，噪声为高斯白噪声。信噪比定义为带通滤波的带宽取为RSN的信号带宽，除了RSN和噪声功率外没有其他的先验信息。每种信号在-10～10dB的RSN范围内进行仿真，其结果如图3所示。各种调制方式的共同特点是随着信噪比的增大，正确识别的概率随之增加。

图3 不同RSN下的调制识别正确率

4 结束语

在通过对通信信号特征的分析，区分出各个通信信号的之间的不同点，采用已有的特征提取优化，小波变化等方法，对PSK、FSK、QAM和ASK4种数字通信信号的调制方式进行仿真识别。采用Matlab进行仿真分析，在AWGN信道下，当信噪比不低5dB时，识别的正确率较高。在仿真中发现当通过设置适当的参数和门限值，可以消除部分参数对识别的影响，但信噪比对识别的正确率影响较大，只有提高信号信噪比，才能够正确地自动识别调制信号类型。

[1]张辉，曹丽娜.现代通信原理与技术[M].西安:西安电子科技大学出版社，2002.

[2]李杨，李国通，杨根庆.通信信号数字调制方式自动识别算法研究[J].电子与信息学报.2005，32（2）:39-41.

[3]陈琦珍.数字调制信号方式的小波识别算法研究[D].南昌大学;2007.

[4]冯祥，李建东.调制识别算法及性能分析[J].电波科学学报.2005，20（6）:737-740.