数控管切割机床相贯线切割的研究

何赛松，徐 雷

（四川大学 制造科学与工程学院，成都 610065）

数控管切割机床相贯线切割的研究

何赛松，徐 雷

（四川大学 制造科学与工程学院，成都 610065）

0 引言

桁架结构在现今的许多大跨度的场馆建筑，如会展中心、体育场馆或其他一些大型公共建筑中有广泛运用，它是由管与管相贯搭接后焊接而成的[3]。传统人工切割出管材的相贯线比较困难，而且效率低，精度不高，早已无法满足现代桁架结构制造的要求，迫切需要现代化的数控加工手段来解决这一难题。

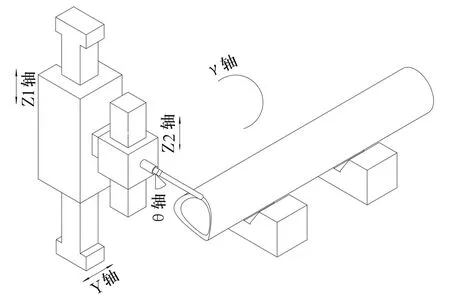
图1 数控管切割机示意图

现在已经有许多研究者开始研究相贯线切割和坡口处理的数学模型[1,2,4]，都是在不同坐标系中求解相贯线坐标，不能直接提供给数控切割机床加工，本文建立了一种在同坐标系下求解相贯线坐标的数学模型，并应用到相应的数控系统中。图1为五轴四联动相贯线切割数控机床的示意图，它采用PLC +运动控制模块+伺服电机进行系统控制，由上位机PC计算出相贯线点的坐标，切割坡口的实际切割角，并将这些数据转化为数控系统实际加工所需要的位置数据，通过PC与PLC通讯给数控机床传递加工数据。五个加工轴定义如表1所示。加工过程的运动为：切管绕ɣ轴做回转运动，同时割咀工作台沿Y轴和Z2轴做直线运动切割出相贯线，割咀绕θ轴做摆动，Z1为一确定值(切割半径与割咀长度之和)，使在切割相贯线的同时切割出坡口，一次定位安装完成管切割，减少多次切割的加工误差和定位误差。

表1 各数控轴的定义

1 相贯线坐标计算

1.1 计算切管母线方程

本文以2管相贯为例，将坐标原点设在切管轴线与交管轴线的交点处，以切管轴线为Z轴，以交管轴线和切管轴线组成YOZ平面，按右手螺旋法则建立计算坐标系。

d —— 切管外径；

t —— 切管壁厚；

N——切管内壁圆周细分点数；

则该切管的母线方程为

1.2 计算交管外壁方程

D1 —— 交管外径；

α—— 交管与切管的轴交角；

则交管1的外壁方程为

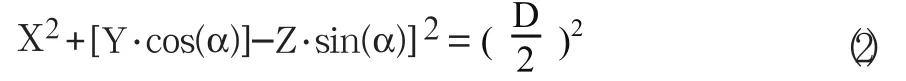
1.3 求解相贯线

联立切管母线方程与交管外壁方程，可求得各条切管母线与交管外壁的交点，可以得到2组Z坐标值，根据最大Z坐标原则，Z值最大的点（X，Y，Z）就是所需的相贯线上的点，平滑地连接这些点就能精确地构成相贯线。

2 坡口处理

根据焊接工艺要求，为保证构件的强度和避免较大的角焊缝尺寸，中厚板接头都要进行开坡口焊接，因此，切割管件时不仅需要相贯线的坐标，还要计算出机床切割时的割咀的摆角。

2.1 参考面和参数值定义

根据求出割咀在切割管材时的摆角，现定义参考面和参数值如表2所示。

表2 各参数值和参考面的定义

2.2 实际切割角计算

由交管方程分别求对X，Y，Z的偏导，可得出在相贯线上的点(x，y，z)处，交管切平面的法向量为（x，cos(α).(y.cos(α)-z-sin(α)，-sin(α).(y.cos(α)-z-sin(α)）。

在切管内壁与交管外壁的相贯线上的点（x，y，z）处的两面角ψ(支管切平面与交管切平面的夹角)为：

坡口角φ根据两面角ψ的大小取值，根据API标准[7]：

割咀在切管轴剖面内绕θ轴的摆动的角度，即实际切割角ω的计算公式为：

实际的切割过程是割咀沿外表面运动的，在这一过程完成相贯线和坡口的切割，坡口角是由实际切割角ω来保证的，ω是割咀在切割轴剖面内的摆动来实现的，再由根据数控切割机床的轴定义，就可计算出各个轴的加工数据。

3 运行实例

现有一个两管相贯的模型，切管外径为80 mm，壁厚为6 mm，交管外径为100 mm，两管轴交角为45°。通过上位机的VB程序，计算出相贯线的点坐标、两面角、坡口角度和实际切割角数据。用MATLAB画出的内外相贯线展开图，如图2所示，两面角、坡口角和实际切割角如图3所示。计算出的结果，转换为数控机床实际切割的数据如表3所示。

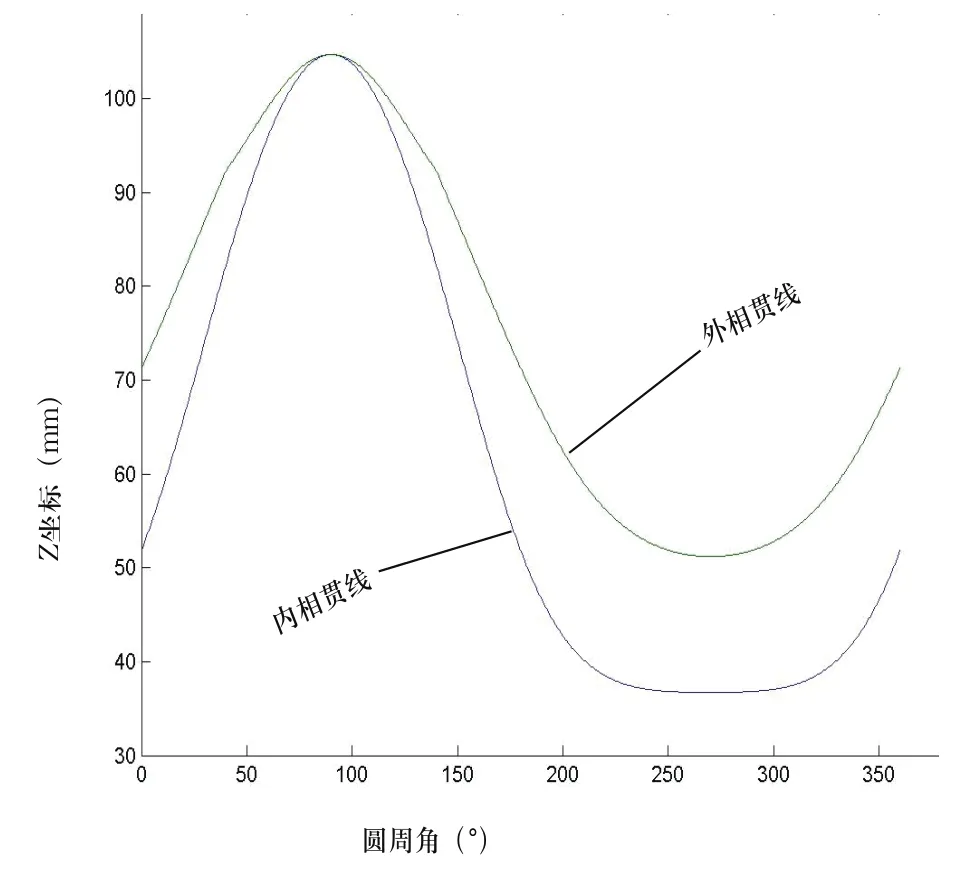
图2 内外相贯线展开图

图3 两面角，坡口角，实际切割角

表3 提供给数控机床实际加工的各轴数据

4 结论

通过实例，验证了数学模型的正确性和有效性。应用在五轴四联动数控机床切割管材，可以满足加工多管相贯相贯线和坡口的需要。数学模型以后可以向其他不规则相贯的情况研究，使一台数控设备加工出各种相贯线和坡口，以满足不同客户多样化的需求。

[1]肖聚亮,阎祥安,王国栋,贾安东.火焰数控切管机割炬轨迹研究及仿真[J].机械工程学报,2005,41(4): 234-238.

[2]李宝清,贾安东.多管、板相贯坡口切割的数学模型[J].天津大学学报(自然科学与工程技术版),2000,33(5):583-586.

[3]王建明,苏永琳.空间多管相贯计算机放样的新算法[J].山东大学学报(工学版),2005,35(6):29-45.

[4]聂晓根,刘艳斌,曾露莎.管件数控火焰切割割炬轨迹建模[J].工程图学学报,2008,29(3):145-150.

[5]谢新房,王国栋.多管相贯焊接坡口数控切割研究[J].工程图学学报,2007,28(4):150-155.

[6]葛国政.数控管子相贯线火焰切割机的研制[J].焊接技术,2006,35(2):45-47.

[7]黄振山,王国栋,王刚.管端焊接坡口数控切割研究[J].制造业自动化,2005,27(9):34-41.

Cutting intersection line by the CNC pipe cutting system

HE Sai-song, XU Lei

为了满足数控切割管材的需要，构建了一种计算相贯线和坡口的数学模型。该模型首先在同个坐标系中建立圆柱管数学方程，计算出切管内相贯线上点的坐标数据，然后根据坡口角度，计算出数控机床割咀摆动角度，引导数控切割机床正确进行相贯线和坡口一次成型的切割。通过应用实例，验证了该数学模型的可行性和有效性，研究成果已应用于五轴数控火焰切割机床数控系统的开发中。

相贯线坐标计算；坡口处理；数控系统

何赛松（1986 -），男，四川攀枝花人，在读研究生，主要从事数控技术与自动化的学习研究。

TG48

A

1009-0134(2011)4(上)-0065-03

10.3969/j.issn.1009-0134.2011.4(上).21

2010-10-13

四川省科技支撑计划（2008ZO0001）；成都市科技支撑计划项目（09RKYB980ZF-033）