高速加工程序段间转接速度算法的研究
李 丹
(四川建筑职业技术学院,德阳 618000)
高速加工程序段间转接速度算法的研究
李 丹
(四川建筑职业技术学院,德阳 618000)
0 引言
高速加工理论是德国切削物理学家萨洛蒙(Salomon)博士于1931年提出的。该理论表明:当切削速度vc增大到某一数值后,可使切削温度下降,切削力大幅减少,并能提高工件表面的加工质量,省去后续光整工序。由于高速加工能成倍提高生产效率,因此成为制造技术中引人注目的一项新技术。
在高速切削所包含的诸多基础理论与关键技术中,数控系统的程序段间拐角速度的处理功能是一个重要内容。
传统数控系统对每一个程序段进行加减速,当达到定位精度,移动轴速度减小为零。这样必然导致电机频繁加减速,进给速度下降,效率低,且影响加工质量。因此建立段间速度的转接控制是高速加工的必然。
在数控高速加工中,不同程序段间进给速度的大小和方向是不同的。当加工区域内存在尖锐拐角或高曲率路径时,以编程速度F进给,会产生过切。需要以规划的控制算法,平稳降速,在允许的误差范围内保证进给速度的最大化,进一步提高加工的效率和精度。
本文讨论了程序段间速度转接控制的各种算法的优缺点以及应用场合。
1 程序段间拐角速度的控制算法
目前采用的常用方法有:直接转接法、圆弧过渡法、弓高误差约束算法、机床动力学约束算法等。
1.1 直接转接法
直接转接法以直线小线段为研究对象,建立了小线段高速加工时段间拐角进给速度的约束条件。
在图1中,设运动中运动速率不变,只是速度矢量方向变化。因此p2点会因速度方向变化而产生加速度。
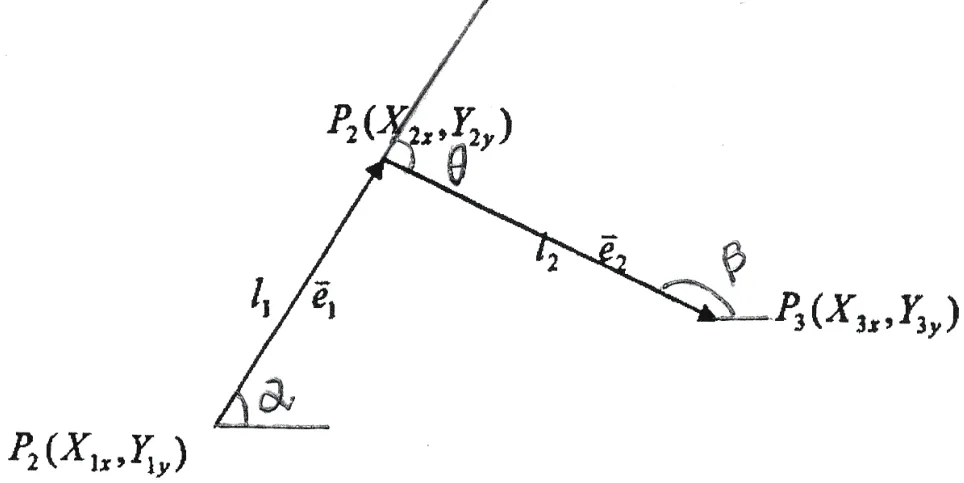
图1 直线与直线直接转接
设p2点的速度,与X轴的夹角为α,与X轴的夹角为β,相邻两直线与之间的夹角为θ,γ 为加速度与X轴的夹角。
当速度方向发生变化时,速度在X轴、Y轴的变化量为v2x,v2y。

上式中,取Δt为一个插补周期To,amax为机床的最大加速度,amax由电机功率和机械传动系统共同决定,也是一个确定值。如果段间的速度大小有变化,则有加速度为ax,则


图2 程序段间圆弧过渡
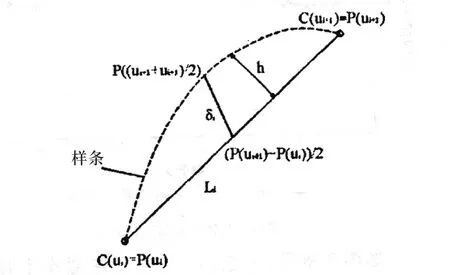
当θ=0或很小时,转接速度v2可以很大,大于编程速度F(但v2不能高于系统设定的最大进给速度,即v2 圆弧过渡法是在程序段段间用圆弧来处理拐角的速度。通过限制小圆弧的最大法向加速度来限制拐角的速度,同时考虑精度的影响。 根据运动学规律,圆周运动的进给法向加速度: 而过渡圆弧半径r的大小则由精度确定。如图2所示,过渡圆弧的的圆心在两直线夹角θ的补角的角平分线上。拐点到圆弧的最短距离为δ(即精度)。δ的值可有系统设定。 由(4)式可求得r,代入(2)式求vmax公式,进而由(3)式得到段间的转接速度。 圆弧过渡法能提高转接速度和加工稳定性,算法简单,易实现。 图 3 弓高误差的近似算法 弓高误差约束的算法适用于样条曲线插补。目前在CAD领域广泛采用B样条、三次样条、NURBS等参数曲线和曲面描述复杂的零件轮廓。数控系统直接接受样条信息,生成曲线轨迹。在每一个插补周期中都是以一个直线代替曲线弧进行处理,因此有弓高误差。 所谓弓高误差,是指一段曲线上连接两端点的弦与弧的最大法向差(如图3所示)[4]。直接计算很复杂。目前有两种近似算法:一是直接近似法,利用弦和弧的中点连线代替弓高误差。由于弦长很少,近似是合理的;二是用圆弧逼近,用局部的圆曲率近似样条曲线的曲率,涉及曲线导数的计算,运算量较大。因此目前多采用第一种方法。 变换公式可得到进给速度与 设δmax是系统允许的最大弓高误差,则 该方法通过建立机床数控驱动系统的动力学模型,得到各轴的运动约束方程,进一步得到进给速度的约束。 1.4.1 机床动力学方程的建立 经实验验证,数控机床加工时,在各项动力学参数中有三项对机床的动态特性影响较大。1)由于进给速度方向和大小改变产生的惯性力;2)切削进给抗力;3)各部件间的摩擦力。 根据凯恩方程的定义,系统相对于某一独立速度的广义主动力和广义惯性力之和为零[2]。由此可以分别建立数控机床各轴的进给系统动力学方程[3]。 式中: Mx,My,Mz---电动机作用于各轴滚珠丝杠的驱动力矩 Ffx,Ffy,Ffz---机床床身对各轴工作台的摩擦力 Fcx,Fcy,Fcz---各轴切削力; lfx,lfy,lfz---各轴滚珠丝杠的导程; m---工作台及工件质量; J--各轴的转动惯量; 1.4.2 各轴加速度的计算 设曲线加工的路径表示为r(u)={x(u),y(u),z(u)}u-曲线的参数 其中 设v(u)为加工曲线的进给速度,vx、vy、vz为 x轴的进给速度分量,则有 式中tx(u)、ty(u)、tz(u)---曲线任意点单位切向矢量在对应轴的分量,有 设x、y、z轴加速度为ax(u),ay(u),az(u); kx、ky、kz——曲线上任意点的曲率在x,y,z轴上的分量 等号右边第一项表示进给方向改变时产生向心加速度在x,y,z轴上的分量,第二项表示进给速度大小改变时切向加速度在x,y,z轴的分量。 1.4.3 摩擦力方程 当系统以高于临界速度运动时,特别是在高速加工情况下,滑动摩擦力与所受压力及滑动速度有关[2]。可摩擦力大小表示为: 式中:Cf——摩擦系数;Ni——工作台所受压力; i——x,y,z轴1.4.4 切削力方程 切削力在其他参数一定时大小与进给速度成正比[2]。 式中:Fci——切削力;Cci——切削力系数 1.4.5 驱动力矩方程 ML——负载转矩;ks——转矩系数(0 1.4.6 最高进给速度约束方程 当机床处于正常工作状态时,应满足进给轴的加速度小于最大进给加速度;工作功率小于额定功率;最高允许进给速度小于进给电机额定转速下的最高进给速度。即 式中:nMi——各轴电动机的额定转速 把式(7)、(8)、(9)、(10)带入(6)可得x轴的运动约束方程: 同理可得y轴和z轴的动力学方程,并通过该方程可以解出vx的大小。 该算法通用性强,但涉及的计算复杂,其中对于曲线各点的加速度的计算,可以先对危险点做筛选,再进行加速度的计算,以减少计算量。 程序段间转接速度的控制是高速加工中关键技术之一,直接影响数控机床的加工精度加工效率。文中分析了几种不同程序段间转接速度的算法的特点及其适用的场合。 [1]王宇晗,肖凌剑,等.小线段高速加工速度衔接速度数学模型[J].上海交通大学学报,2004,38(6):901-904. [2]何莹.高速加工插补算法动力学行为分析与评价[D].武汉:华中科技大学,2005. [3]彭芳瑜,何莹,等.NURBS曲线机床动力学特性自适应直接插补[J].华中科技大学学报:自然科学版,2005,33(7):80-83. [4]范永强.基于DSP的NURBS直接插补技术研究[D].浙江:浙江大学,2010. [5]徐志明,冯正进,等.连续微小路径段高速自适应前瞻插补算法[J].制造技术与机床,2003,(1):31-34. [6]张得礼,周来水.数控加工运动的平滑处理[J].航空学报,2006,27(1):126. High-speed processing procedures section connecting speed between the algorithm LI Dan 文中详细分析了数控高速加工中程序段间转接速度的控制的几种算法---直接转接法,圆弧过度法,弓高误差约束法,机床动力学和运动学算法的特点及适用场合。 高速加工;程序段间转接速度算法 李丹(1970 -),女,讲师,工程硕士,研究方向为数控加工技术、数控维修、控制工程。 TP273 A 1009-0134(2011)5(上)-0055-04 10.3969/j.issn.1009-0134.2011.5(上).20 2010-11-011.2 圆弧过渡法

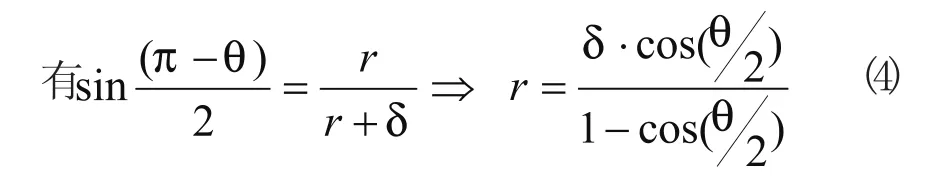
1.3 弓高误差约束的算法

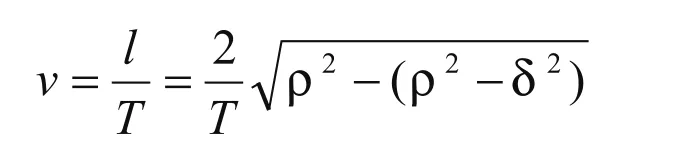
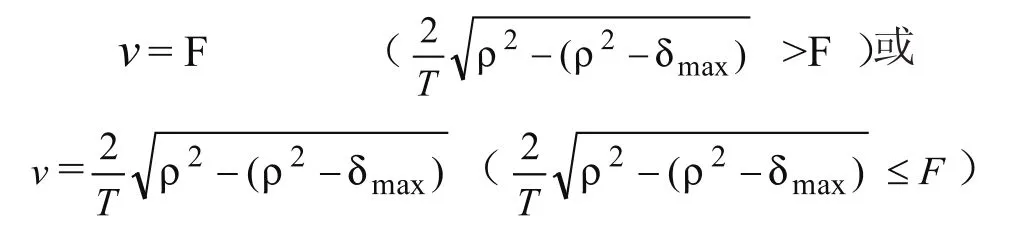

1.4 基于机床运动学和动力学约束方程的算法

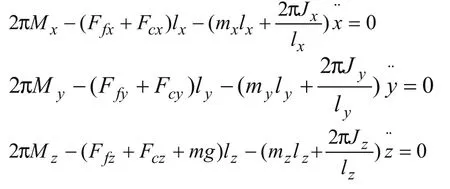


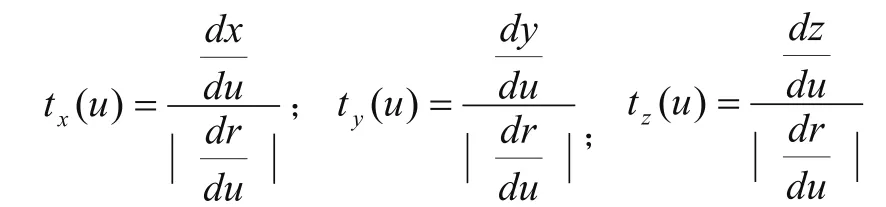

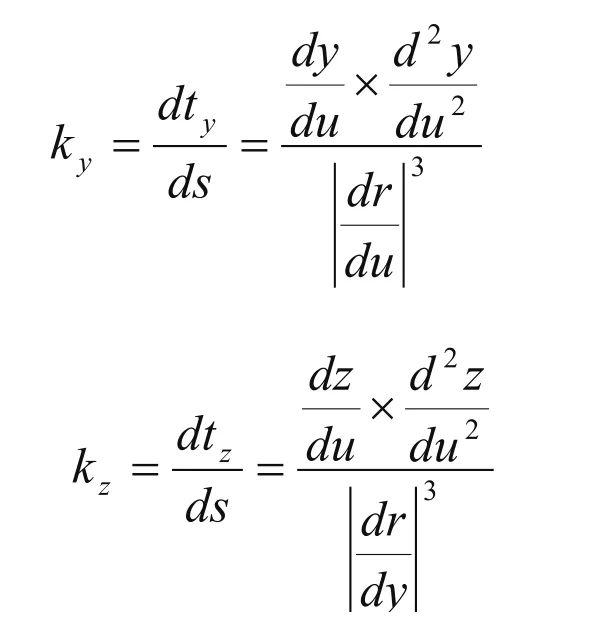






2 结束语

