基于趋近律滑模的台车式倒立摆系统控制研究*

宋莹 樊立萍 张君

1 引言

滑模变结构控制是前苏联学者 Emeleyanov、Ut-kin、Itkin在20世纪60年代初提出的一种控制方法[1],其本质是一类特殊的非线性控制，且非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的“结构”并不固定,而是可以在动态过程中，即根据系统当前的状态有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动。滑模控制的优点是能够克服系统的不确定性, 对干扰和未建模动态具有很强的鲁棒性,尤其是对非线性系统的控制具有良好的控制效果[2]。近年来,在机器人控制、电机伺服控制等复杂的非线性控制系统中,滑模变结构控制因为其强鲁棒性而得到广泛应用和发展。因此,越来越受到人们的重视。

滑模运动包括趋近运动和滑模运动两个过程[3]。系统从任意初始状态趋向切换面，直到到达切换面的运动称为趋近运动，即趋近运动为s→0的过程。根据滑模变结构的原理，滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，而对于趋近运动轨迹未作任何限制，采用趋近律的方法可以改善趋近运动的动态品质。

趋近律方法是滑模变结构控制的一种典型的控制策略，它不仅可以对系统在切换面附近或沿切换面的滑模运动段进行分析，而且可有效地对系统趋近段的动态过程进行分析和设计，从而保证系统在整个状态空间内具有良好的运动品质。本文提出了一种指数趋近律，当正常运动段远离切换面时，能快速地趋向切换面；当运动接近切换面时，趋近速度又大大降低。与等速趋近律相比，其过渡时间、系统的抖动以及所需的控制力都能进一步减小。

为了验证所提出的指数趋近律滑模控制的有效性，本文对一级台车式倒立摆模型[4]进行分析和建立数学模型，然后利用滑模变结构控制对小车的位置控制问题、摆角度控制问题和控制器的输出进行详细的研究。在Matlab/Simulink仿真环境下进行仿真实验。

2 台车式倒立摆系统

倒立摆系统的控制问题一直是控制研究中的一个典型问题。控制目标是通过给小车底座施加一个控制量，使小车停留在预定的位置，并使竖立的杆不倒下，即不超过一预先定义好的垂直偏离角度范围。图1为一级倒立摆的示意图，小车的质量为M，摆的质量为m，小车的位置为x，摆的角度为α，杆长为2a 。

图1 台式车倒立摆系统

倒立摆的状态方程为：

其中：

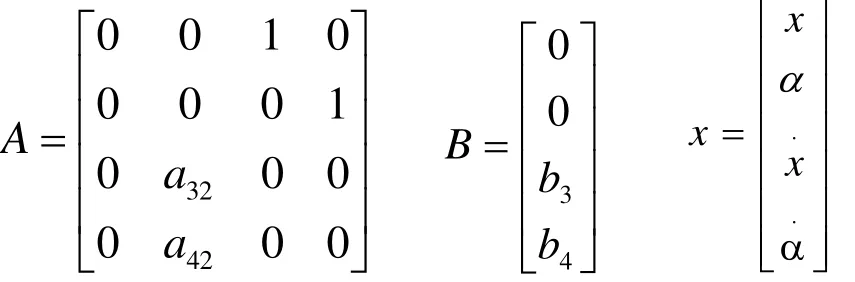
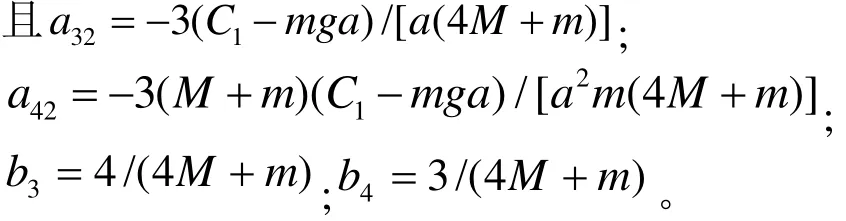
其中， C1为弹性硬度， g = 9 .8 m /s2,u和 f ( t )分别为控制输入和干扰力，且f(t)≤f0，f0为常数。

3 滑模变结构控制器的设计

文中采用了两种变结构的控制方法实现了台车式倒立摆小车和摆角的控制。在该控制律中，采用了Ackermann公式设计滑模控制律中的C值。

考虑如下系统：

设计滑模变结构控制的任务在于选择滑模面s，即确定C并确定控制U，使闭环系统中滑模面上存在滑动模态，且所有相轨迹在有限时间内到达s上的滑动模态区域并保证滑动模态渐近稳定且具有良好的品质[5]。

① 等速趋近律

其中，常数ε表示系统的运动点趋近切换面s= 0 的速率。ε小，趋近律速度慢；ε大，则运动点到达切换面时将具有较高的速度，引起的抖振也较大。

② 指数趋近律

式中，s = - k s ，是指数趋近项，其解为s = s ( 0 )e-kt。

指数趋近中，趋近速度从较大的值逐步减小到零，这不仅缩短了趋近时间，而且运动点到达切换面时的速度也很小。对单纯的指数趋近，运动点逼近切换面是一个渐进的过程，不能保证有限时间内到达，切换面上也就不存在滑动模态了，所以要增加一个等速的趋近项 s˙ = -εsgn(s)，当s接近于零时，趋近速度是ε而不是零，可以保证有效时间内到达。

在指数趋近律[6]中，为了保证快速趋近的同时削减抖振，可在增大k的同时减小ε。控制律取:

4 仿真结果

为了验证所设计的指数趋近律滑模控制的有效性，对一级台车式倒立摆系统进行了一系列仿真实验。

倒立摆系统的状态方程如式（1）所示。倒立摆参数取为： g = 9 .8m/s2（重力加速度）， M = 5.0kg（小车质量）， m = 1 k g(杆的质量)， a = 0 .6m(杆的半长)， C1= 1 ， f ( t ) = 0.4sin(3t )。

仿真中所用的采样时间T = 0 .02s，仿真时间为30s。初始条件取 x (0) = 0 . 4，α(0)=0.3，x˙(0)=0，α˙(0) = 0,其中摆动角度单位为弧度。

在控制系统中，由于n=4，故取λ1=-1，λ1= -2，λ1=-3，根据Ackermann公式设计滑模控制律中的 C 值，即根据式(2)，可得CT=[-4 . 7 673, 48.3564, - 8 . 7 401, 18.6534]。

在仿真程序中，图2采用等速趋近律，图3采用指数趋近律，ε=5，k=10仿真结果如下图2、图3所示。

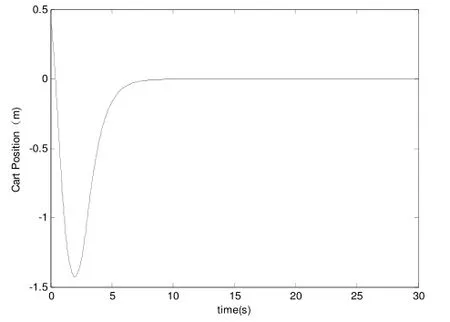
图2 a) 小车位置控制

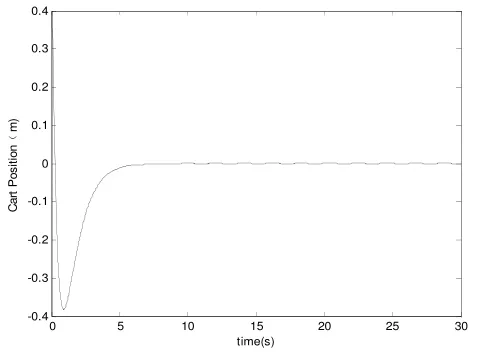
图3 a) 小车位置控制

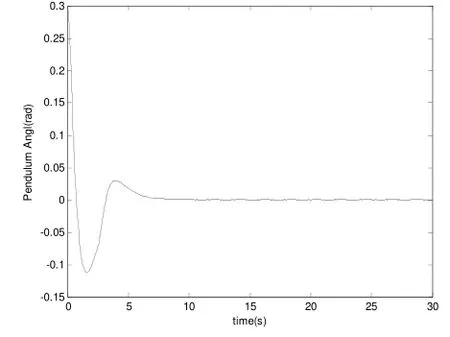
图2 b) 摆角度控制

图3 b) 摆角度控制

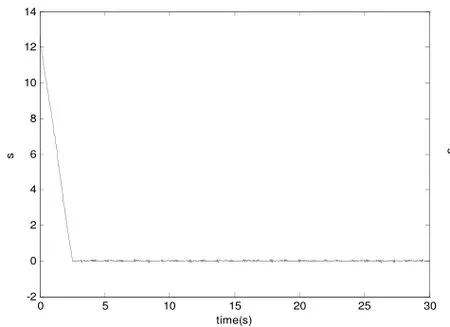
图2 c) 切换函数

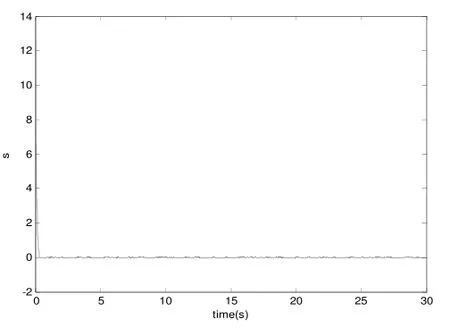
图3 c) 切换函数

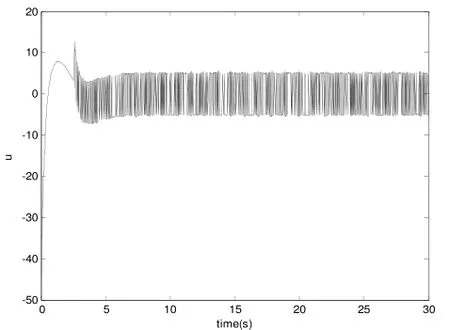
图2 d) 控制器输出

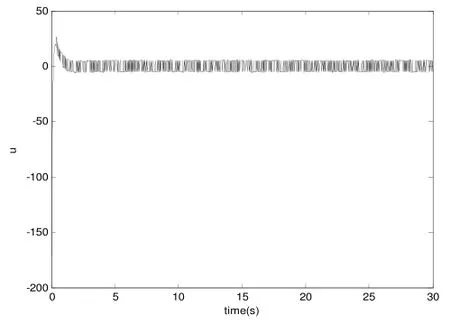
图3 d) 控制器输出

从仿真结果可以看出，本文提出的指数趋近律方法设计的滑模控制器不仅使系统具有良好的控制性能，缩短了趋近时间，而且更好地消除了常规滑模变结构控制所固有的高频颤动现象，对模型不确定性和外部干扰具有较强的鲁棒性，同时保证了系统在整个状态空间内具有较好的运动品质，使系统快速到达滑模面。

5 结束语

本文用两种趋近律方法设计的滑模控制器应用到台车式倒立摆中，从仿真结果可以得出：指数趋近律方法设计的滑模控制器不仅缩短了过渡时间，减少了常规滑模变结构控制所固有的高频颤动现象，而且改善了系统的控制性能，提高了系统的鲁棒性。

[1] Emelyanov,SVV.ariable Structure Control Systems.Nauka.Moscow, 1967 (In Russian).

[2] 陈峰.滑模变结构控制理论及其在机器人中的应用研究[D].江南大学,2008.

[3] 孔祥梅,李宏光.滑模控制中一类趋近律的改进[J].鞍山科技大学学报,2007,(04).

[4] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.

[5] YUAN,Xing-zhong,JIANG,Xin-jian.Stabilizing control of inverted pendulum using sliding modescheme[J].Control Theory & Applications,2004,21(5):721-723.

[6] 张昌凡,何静.滑模变结构的智能控制理论与应用研究[M].北京:科技出版社,2005.