全相位多维多抽样率数字滤波器设计

侯正信，刘建忠，宋占杰，杨爱萍

(天津大学电子信息工程学院，天津 300072)

全相位多维多抽样率数字滤波器设计

侯正信，刘建忠，宋占杰，杨爱萍

(天津大学电子信息工程学院，天津 300072)

基于一维全相位数字滤波器(APDF)，提出了通用的全相位多维多抽样率数字滤波器设计方法. 该方法适用于抽取/内插矩阵为任意有理数情况，能够保持奈奎斯特特性和零相位特性，可将一维APDF的优良特性继承到多维滤波器. 由一维 APDF的波纹和过渡带参数，导出了结果滤波器的通带、阻带波纹和过渡带向量的估算公式. 另外，研究了一种根据理想通带参数寻找对应抽取/内插矩阵的方法，并给出了抽取/内插矩阵分别为整数和有理数时的2个实例.在滤波器长度相同的情况下，与传统方法相比，所设计的全相位多维多抽样率滤波器过渡带略宽，但通带波纹和阻带波纹更小，阻带衰减更大，具有良好的幅频特性.

多维多抽样率；有理数抽取/内插矩阵；加窗全相位；多维抽取；任意平行六面体

多维数字滤波器是多维多抽样率信号处理[1]和多尺度几何分析[2]的重要基础.目前常用的多维滤波器设计方法主要有窗函数法[3]、McClellan变换法[4-5]和最优化法[6-8].窗函数法由于截断产生吉布斯效应，需要采用变化平滑的多维窗函数，这样既增加了过渡带宽度也不能彻底消除吉布斯效应.McClellan变换法是一种应用广泛的多维滤波器设计方法，特别是关于二维滤波器的设计已经相当成熟[4]，但在设计更高维的滤波器时需要具备很多的对称性约束条件，变换函数系数一般较难确定，目前研究高效灵活的高维McClellan变换仍是一个重要热点[5].最优化法包括Minmax最优化方法[6]、SVD 方法[7]和频域直接优化法[8]等.但是设计 FIR滤波器时只满足低性能要求的滤波器，高性能要求的滤波器设计需要很高的阶数.

文献[9]阐述了一种由一维滤波器通过简易变换衍生出多维多抽样率滤波器的方法，具有一定的通用性，但是所设计的滤波器性能由一维原型滤波器决定.因此，如何找到性能优良的一维原型滤波器是采用这种方法的关键.全相位数字滤波器(all phase digital filter，APDF)是一种新型的零相位滤波器，它采用重叠数字滤波的思想，有效地克服传统频域滤波对信号采用分段处理所产生的吉布斯效应，可分别基于 DFT 域[10]、WHT 域[11]和 DCT/IDCT 域[12]进行设计.文献[13-14]分别推导了基于 DFT域和 IDCT域的一维加窗全相位滤波器的设计公式，通过加窗用稍宽的过渡带换取了十分平坦的通带和阻带特性，改善了滤波器性能.目前，对于多维 APDF的设计还缺少系统的研究.文献[15-16]讨论了直接由二维列率矩阵设计某些具有特定频率响应的不可分离二维 APDF，例如钻石形、扇形滤波器等，但仅适用于设计不加窗(相当于加矩形窗)的APDF.若设计二维加窗APDF，由于窗函数的影响，不便直接由二维列率矩阵设计.本文提出一种通用的全相位多维多抽样率滤波器的设计方法，可基于 DFT、WHT和 DCT/IDCT等不同变换域，设计具有任意平行六面体通带区域的多维APDF.基于 IDCT域的一维加窗 APDF具有更好的幅频特性[14]，因此，本文将其作为一维原型滤波器进行多维多抽样率数字滤波器设计.

1 基于IDCT域的一维加窗全相位滤波

图1 基于IDCT域加窗APDF的直接列率域实现Fig.1 Direct sequence realization of windowed APDF Fig.1 based on IDCT

2 全相位多维多抽样率数字滤波器设计

2.1 多维多抽样率数字滤波器

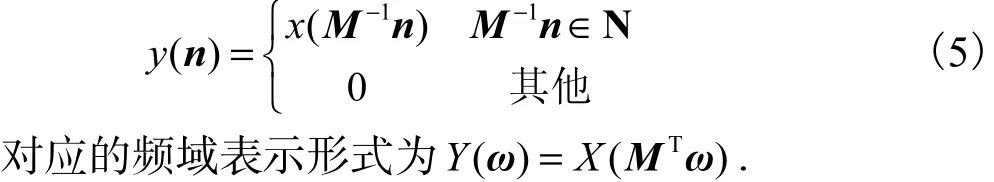
为防止M倍抽取引起的频谱混叠，通常先用抽取滤波器对信号 x(n)滤波，然后再进行抽取.而M倍内插时，则需要将内插信号 y(n)通过内插滤波器，去除M倍内插产生的镜像频谱.因此，无论抽取还是内插，都需要一个多维抽取/内插滤波器，统称为多维多抽样率数字滤波器 H(ω)，具有平行六面体通带区域[9]

2.2 与一维原型全相位数字滤波器的关系

2.3 抽取/内插矩阵H为任意有理数的情况

推广整数抽取/内插矩阵M为非奇异有理数矩阵H，由于任何无理数矩阵都能够用有理数矩阵来近似，S P D(π H-T)可以表示任意平行六面体形状的通带区域.

考虑一个多维理想低通滤波器 G (ω)，它具有通带区域 S PD(π H-T)，亦即

2.4 设计步骤

总结第2.2和2.3节，设计通带区域为 S PD(π H-T)的全相位多维多抽样率数字滤波器有以下5个步骤.

3 结果滤波器性质分析

3.1 通带、阻带波纹和过渡带

因为实际中滤波器 H(s)(ω)是非理想的，所以步骤(4)和(5)中多维抽取会造成通带和阻带的频谱混叠.下面借鉴文献[9，18]中的方法，讨论通带波纹、阻带波纹和过渡带向量的估算.假设一维原型滤波器P(ω)的通带波纹δ1，阻带波纹δ2.利用式(9)和式(10)易知，H(s)(ω)的通带和阻带的幅频响应分别满足

3.2 零相位特性

APDF可以有效地克服吉布斯效应，在时域满足实偶对称，是零相位数字滤波器的一个子集[10]，对应频率响应亦为实偶对称，没有相位畸变，在图像处理方面具有重要意义.假设一维原型滤波器 p (n)为APDF，则满足 p (n) = p ( - n )，由式(10)可知 h(s)(n)=h(s)(- n).再进行多维抽取可得： g ( n) = c h(s)(Ln)=ch(s)( -Ln) = g (- n).因此，本文所设计的结果滤波器 g (n)也具有零相位特性.

3.3 保持奈奎斯特特性

奈奎斯特滤波器的脉冲响应 f (n)满足条件：f(M n) = 0，n≠0，M为某一整数矩阵.这种滤波器也称为M带滤波器.作为内插滤波器时，奈奎斯特滤波器具有保持原有采样值不变的优点，没有抽样值之间的相互干扰.本文的设计方法可以保持奈奎斯特特性.更准确地说，假设一维原型滤波器 p (n)为奈奎斯特滤波器，即 p (J ( M ) n) = 0，n ≠ 0 .利用式(10)，得h(s)(J(M )n) = 0，n≠0.则h( M n ) =c0h(s)(Mn)=c0h(s)(J(M )n)=0，n≠0.因此，h(n)也是奈奎斯特(M带)滤波器.此外，如果把奈奎斯特特性推广到有理数情形：不论Hn是否为非零整数向量都满足f( H n) = 0，即H带特性.可以证明结果滤波器 g (n)同样满足奈奎斯特特性.

3.4 因果性

假设从一维因果滤波器 p (n)开始设计，式(10)所示的可分离多维滤波器 h(s)(n)显然是因果滤波器(即当且仅当ni为非负值时，h(s)(n)为非零值).MˆL抽取 h(s)(n)产生的结果滤波器 g (n)的因果性由抽取矩阵MˆL决定.当且仅当矩阵(L)-1的所有元素为非负时，等价于矩阵H的所有元素为非负值，g(n)为因果滤波器.而对于含有负数元素的H矩阵，最后所得结果滤波器 g (n)不能保持因果不变性.

3.5 通用性

第 2.4节已经说明了如何根据抽取/内插矩阵 H设计全相位多维多抽样率数字滤波器.但是实际设计滤波器时，有时仅给定通带而非矩阵H.因此，需要研究利用理想通带参数求取对应矩阵H的方法，以便设计各种滤波器.假设每一个平行六面体区域的通带都可表示为

式中矩阵P的列向量可称为生成向量.图2显示了二维平行六面体通带区域及其生成向量 p0和 p1.对比式(28)和 S PD(π H-T)，若令

则矩阵 H即为所求矩阵.因此，本文设计方法具有广泛的通用性.

图2 二维平行六面体的生成向量Fig.2 Generating vectors of a 2D parallelepiped

4 设计实例和讨论

4.1 H为整数矩阵

与本文方法进行对比，采用切比雪夫等波纹逼近方法设计与 PN(ω)具有相同长度的原型滤波器 P (ω)，最后所得的结果滤波器 H(ω) 如图 5(c)、(d)所示.由图 5可知，本文方法所设计的结果滤波器 H(ω)通带和阻带更加平坦，通带波纹和阻带波纹更小，通带边缘没有明显的吉布斯效应，阻带衰减更大，但是过渡带不如切比雪夫等波纹逼近法陡峭.

表 1中列出了本文方法和切比雪夫等波纹逼近方法设计时的一维原型滤波器和结果滤波器的通带波纹、阻带波纹和过渡带等情况.由表1易知，2种方法所设计滤波器的实际值均小于按照式(22)、(23)和式(26)所计算的估计值.由图 5和表 1可知，与传统切比雪夫等波纹逼近方法相比，本文方法设计的加窗全相位多维多抽样率滤波器过渡带略宽，通带特性十分平坦，阻带具有更大的衰减，具有优良的阻带和通带特性.

图3 例1中滤波器H(ω)的理想通带SPD(πH-T)Fig.3 Desired passband SPD(πH-T) of filter H(ω) in example 1

图4 PN(ω)的幅度响应Fig.4 Magnitude response of PN(ω)

图5 多维多抽样率数字滤波器H(ω)的幅度响应Fig.5 Magnitude response of multidimensional multirate filters H(ω)

表1 例1中一维原型滤波器和结果滤波器的通带波纹、阻带波纹和过渡带Tab.1 Passband and stopband ripples and transition band of 1D prototype and resulting filters in example 1

4.2 H为有理数矩阵

假设需要设计的滤波器 g (n)的理想通带区域如图 6灰色阴影部分所示，用 S PD(π H-T)表示，其中有理矩阵H及其左MFD为

图6 例2中滤波器G(ω)的理想通带SPD(πH-T)Fig.6 Desired passband SPD(πH-T) of filter G(ω) in Fig.6 example 2

图7 例2中结果滤波器G(ω)的幅度响应Fig.7 Magnitude response of resulting filter G(ω) in design example 2

表2 例2中一维原型滤波器和结果滤波器的通带波纹、阻带波纹和过渡带Tab.2 Passband and stopband ripples and transition band of 1D prototype and resulting filters in example 2

5 结 论

(1) 本文基于一维全相位数字滤波器(APDF)，提出了通用的全相位多维多抽样率数字滤波器设计方法，适用于抽取/内插矩阵 H 为任意有理数的情况.该方法可以设计具有任意平行六面体通带区域的滤波器，具有广泛的通用性，丰富了多维多抽样率数字信号处理理论.

(2) 所设计滤波器具有零相位不变性，可以保持奈奎斯特(M带)特性，将一维 APDF的优良特性继承到多维滤波器.当矩阵H的所有元素为非负值时，所得的滤波器保持因果不变性.

(3) 利用一维 APDF的通带、阻带波纹和过渡带，导出了结果滤波器的通带、阻带波纹和过渡带向量的估算公式.研究了一种根据通带参数寻找对应矩阵H的方法，以便设计各种滤波器.

(4) 与传统设计方法相比，在滤波器长度相同的情况下，本文所设计的全相位多维多抽样率滤波器过渡带略宽，通带波纹和阻带波纹更小，阻带衰减更大，具有更平坦的通带和阻带特性.

［1］Law Ka L，Fossum R M，Do Minh N. Generic invertibility of multidimensional FIR multirate systems and filter banks[C]//Proceedings of IEEE International Conference on Acoustics，Speech and Signal Processing.Taipei，China，2009：3385-3388.

［2］Tanaka Yuichi，Ikehara Masaaki，Nguyen Truong Q. Multiresolution image representation using combined 2-D and 1-D directional filter banks[J].IEEE Transactionson Image Processing，2009，18(2)：269-280.

［3］Dembo A，Malah D. Generalization of the window method for FIR digital filter design[J]. IEEE Transactions on Acoustics，Speech and Signal Processing，1984，32(5)：1081-1083.

［4］Chen C K，Lee J H. McClellan transform based design techniques for two-dimensional linear-phase FIR filters[J].IEEE Transactions on Circuits and SystemsI：Fundamental Theory and Applications，1994，41(8)：505-517.

［5］Shyu J J，Pei S C，Huang Y D. 3-D FIR cone-shaped filter design by a nest of McClellan transformations and its variable design[J].IEEE Transactions on Circuits and Systems I：Regular Papers，2010，57(7)：1697-1707.

［6］Charalambous C. The performance of an algorithm for minmax design of two-dimensional linear phase FIR digital filters[J].IEEE Transactions on Circuits and Systems，1985，CAS-32(10)：1016-1028.

［7］Ma Jun，Parhi K K，Deprettere E F. A unified algebraic transformation approach for parallel recursive and adaptive filtering and SVD algorithms[J]. IEEE Transactions on Signal Processing，2001，49(2)：424-437.

［8］Nguyen Truong T，Oraintara Soontorn. Multidimensional filter banks design by direct optimization[C]//Proceedings of IEEE International Symposium on Circuits and Systems.Kobe，Japan，2005，2：1090-1093.

［9］Chen Tsuhan，Vaidyanathan P P. Multidimensional multirate filters and filter banks derived from one-dimensional filters[J].IEEE Transactions on Signal Processing，1993，41(5)：1749-1765.

［10］侯正信，王兆华，杨 喜. 全相位 DFT数字滤波器的设计与实现 [J]. 电子学报，2003，31(4)：1-4.

Hou Zhengxin，Wang Zhaohua，Yang Xi. Design and implementation of all phase DFT digital filter[J].Acta Electronica Sinica，2003，31(4)：1-4(in Chinese).

［11］侯正信，王成优，杨爱萍，等. 全相位沃尔什双正交变换及其在图像压缩中的应用[J].电子学报，2007，35(7)：1376-1381.

Hou Zhengxin，Wang Chengyou，Yang Aiping，et al. All phase Walsh biorthogonal transform and its application in image compression [J].Acta Electronica Sinica，2007，35(7)：1376-1381(in Chinese).

［12］侯正信. 离散余弦列率滤波的卷积算法[J]. 通信学报，1999，20(S1)：211-215.

Hou Zhengxin. A convolution algorithm for discrete cosine sequency filtering[J].Journal of China Institute of Communications，1999，20(S1)：211-215(in Chinese).

［13］侯正信，徐妮妮. 加窗全相位 DFT数字滤波器[J]. 天津大学学报，2005，38(5)：448-454.

Hou Zhengxin，Xu Nini. Windowed all phase DFT digital filter[J].Journal of Tianjin University，2005，38(5)：448-454(in Chinese).

［14］赵黎丽，侯正信. 基于 IDCT域的加窗全相位数字滤波器[J]. 天津大学学报，2006，39(12)：1499-1503.

Zhao Lili，Hou Zhengxin. Windowed all phase digital filter based on IDCT[J].Journal of Tianjin University，2006，39(12)：1499-1503(in Chinese).

［15］徐妮妮，侯正信，王兆华. 纯二维全相位滤波器组及其在图像压缩中的应用[J]. 光电子·激光，2007，18(5)：608-611.

Xu Nini，Hou Zhengxin，Wang Zhaohua. True 2-D all phase filter bank and its application for image compression[J].Journal of Optoelectronics Laser，2007，18(5)：608-611(in Chinese).

［16］郭迎春，侯正信，于 明，等. 最优内插的纯二维小波构造[J]. 光电子·激光，2008，19(6)：795-798.

Guo Yingchun，Hou Zhengxin，Yu Ming，et al. Construction of optimal-interpolating true bi-dimensional wavelets[J].Journal of Optoelectronics Laser，2008，19(6)：795-798(in Chinese).

［17］Chen Tsuhan，Vaidyanathan P P. Role of integer matrices in multidimensional multirate systems[J].IEEE Transactions on Signal Processing，1993，41(3)：1035-1047.

［18］Bamberger R H，Smith M J T. A filter bank for the directional decomposition of images：Theory and design[J].IEEE Transactions on Signal Processing，1992，40(4)：882-893.

Design of All Phase Multidimensional Multirate Digital Filter

HOU Zheng-xin，LIU Jian-zhong，SONG Zhan-jie，YANG Ai-ping
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

A general method for designing all phase multidimensional(MD)multirate digital filter was presented based on one-dimensional(1D)all phase digital filter(APDF)，which is applicable to arbitrary rational decimation/expansion matrix. The resulting MD multirate filters inherit excellent properties，such as zero phase property and Nyquist constraint property，from 1D APDF. Their passband and stopband ripples and transition band vector were estimated in terms of the ripples and transition band of 1D prototype filter. Furthermore，a method of computing the corresponding matrix was studied according to the specifications of the ideal passband. Two design examples were given with integer and rational decimation/expansion matrix respectively. Under the condition of the same filter length，compared with traditional method，the resulting all phase MD multirate filters using the proposed method have better amplitude-frequency response characteristics. Except for slightly wider transition band，the pass band and stopband are much flatter with rather small ripples.

multidimensional multirate；rational decimation/expansion matrix；windowed all phase；multidimensional decimation；arbitrary parallelepiped

TN911.72

A

0493-2137(2011)04-0331-08

2010-01-20；

2010-08-18.

国家自然科学基金资助项目（61002027，60872161）.

侯正信（1945— ），男，教授，博士生导师，zhengxinhou@163.com.

刘建忠，ljzh@tju.edu.cn.