压气机叶片最大挠度相对位置对颤振影响的数值研究

陆庆飞

(中国燃气涡轮研究院，四川 成都 610500)

1 引言

叶片颤振是流动诱发的自激振动，其触发机制与叶片的结构参数和振动叶片的非定常流动状况紧密相关。随着航空发动机向高推重比方向发展，在级负荷增大、叶片相对厚度减小、部件刚性下降等因素的影响下，叶片颤振故障频发，已成为高性能航空发动机研制过程中急需解决的挑战性问题。叶片颤振故障常常造成灾难性的后果，而解决故障要耗费大量的人力、财力。

目前，预测叶片颤振的方法一般有三类：经验法、半经验法和计算流体力学法(即能量法)。经验法通过大量的试验来建立叶片颤振数据库；半经验法从流体力学的基本方程组出发，同时又引入工程试验数据。本文采用的是计算流体力学法，该方法能准确捕捉到叶片表面的压力分布和激波振荡，有助于了解叶片的颤振机理，逐步积累叶片颤振的数据，适合工程应用[1]。

2 计算方法简介

以结构动力学方法(用ANSYS软件)确定叶片振型、自振频率和振幅分布后，假设叶片作简谐振动，得出叶片结构运动方程(体现在网格的运动规律上)。然后将这种位移规律纳入振动叶片的非定常流场数值模拟中，计算叶片上的非定常气动力及气动力所做的功，最后采用能量法来评估颤振发作的几率。能量法采用能量的观点来建立气动弹性稳定性判别原则。当叶片由于某种原因产生振动时，会与周围的气体发生能量交换，如果叶片向气流传递能量，即非定常气动力对叶片做负功，则叶片振动将会衰减；反之，如果叶片从气流中吸收能量，非定常气动力对叶片做正功，则叶片振动会加剧。在忽略机械阻尼时，以一个振动周期内叶片与周围气体吸收能量的正负关系来判断叶片是否颤振，此即本文使用的能量法判定准则[2]。

3 动叶振动分析

取某型压气机第一排转子为研究对象，通过改变造型参数来调节叶片的最大挠度相对位置(分别标为 1，2，3，4，造型参数见图 1)，其他参数基本不变。叶片由钛合金制成，其材料特性为：弹性模量119 GPa，泊松比 0.33，密度 4480 kg/m3。

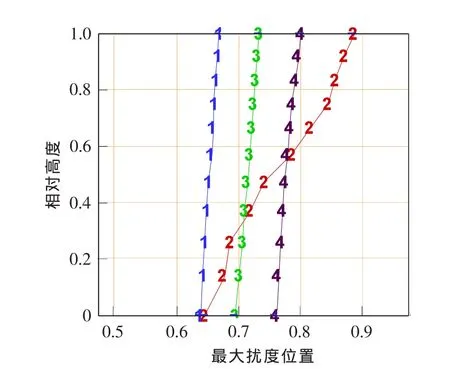
图1 挠度分布Fig.1 Distribution of deflection

在相对换算转速1.0下，由ANSYS分析得到的转子叶片一阶振动频率如表1所示。由表中可以看出，叶片的一阶振动频率随挠度位置的后移而增大。图2给出了四种最大挠度相对位置转子叶片一阶振动位移分布，图中位移量为由ANSYS有限元节点插值转换到非定常绕流计算网格节点上的结果。从图中看，四种最大挠度相对位置下的位移量比较接近。上述对应的数据文件将在颤振分析中使用。

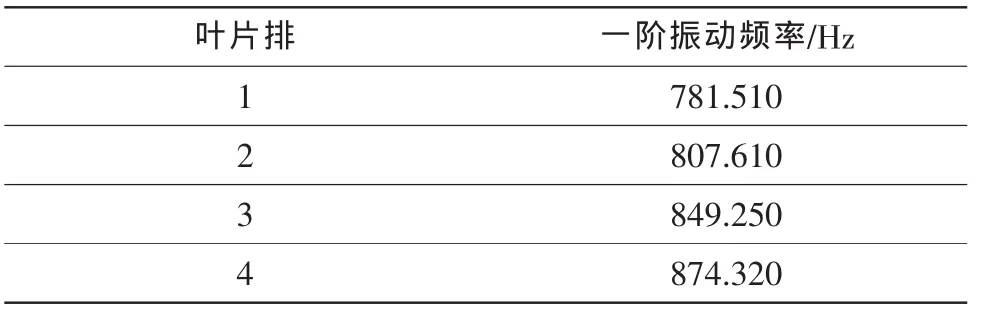
表1 转子叶片一阶振动频率Table 1 The first order vibration frequency of rotor blade

4 颤振分析

对压气机叶片进行结构动力学分析、三维定常分析和颤振分析。根据结构动力学分析得到的叶片自振频率和位移量分布，进行振动叶片三维非定常绕流计算，可获得叶片上非定常平均积累总功率，并由此做出气弹稳定性(颤振)判别[3]。

计算网格：网格数为 31×31×111(周向×径向×轴向)。叶片网格示意图如图3所示。

初场：推进1000时间步，得到收敛的转子全三维定常流场作为初场。

振动叶片非定常绕流分析：做6个振动周期的非定常计算。

图2 转子叶片一阶振动位移分布Fig.2 Displacement distribution of compressor rotor blade at first order vibration mode

图3 叶片网格示意图Fig.3 Computation grid

表2 相对换算转速1.0下的平均积累功率Table 2 Average accumulated power in 1.0 relative corrected speed

根据三维气动计算结果，计算得到该转子在设计点和近喘点的压比，再以此计算叶片的非定常平均积累总功率。表2列出了相对换算转速1.0下沿特性线计算得到的最后一个周期内叶片的非定常平均积累总功率。由表中可以看出，对于一阶振型的颤振，一阶临界点的非定常平均积累功率都为负值，由此判定颤振边界在三维计算的喘振边界以外。在挠度分布比较均匀的叶片排1、3、4中，平均积累功率随挠度位置的后移而减小。由图4、图5可以看出，从叶中到叶尖部分，气流与叶片能量交换比较剧烈；在叶片前缘附近，气流做负功；在靠近尾缘处，气流做正功。在叶根部分，气流基本不做功，气流与叶片能量交换较小。通过比较可以发现，四种情况下，气流做正功的区域大致相当，做负功的区域略有差异。在正功区，气流对叶片排2做功值相对较大；而在负功区，叶片排2叶中区域无明显负功区。其他三种情况比较接近，叶片排3和叶片排4的叶中负功区最明显。因此，在相同压比下，叶片排2叶表的平均积累功率比其他三种叶片排的大，其气弹稳定性比原始叶片差，更容易发生气弹失稳。

5 结论

(1)在压气机气动设计中，最大挠度相对位置会影响动叶的一阶振动频率，但对于风扇/压气机叶片，一阶振动位移分布影响较小。

(2)最大挠度相对位置分布不均匀会大大提高颤振发生的几率，最大挠度相对位置越大，发生颤振的可能性越小。以上结果为压气机叶片设计提供了有益的参考。

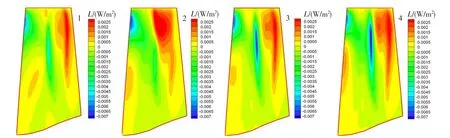
图4 近设计点平均积累功率分布Fig.4 Average accumulated power distribution at near design points

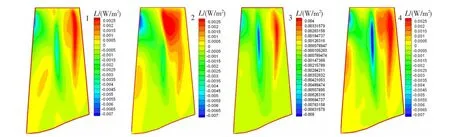
图5 近喘点平均积累功率分布Fig.5 Average accumulated power distribution at near stall points

[1]张扬军，陶德平，周 盛.某型风扇叶片颤振研究[J].燃气涡轮试验与研究，1996，9(2)：5—8.

[2]施永强，杨青真，周新海.风扇/压气机叶型厚度对颤振特性的影响[J].航空学报，2009，30(6)：979—984.

[3]施永强.三维叶片颤振与叶片设计关联性研究[D].陕西西安：西北工业大学，2006.